
Revista Logos, Ciencia & Tecnología. 11(3):18-29 | Septiembre-diciembre 2019
http://revistalogos.policia.edu.co
Artículo de Investigación
Didáctica y desarrollo del pensamiento lógico matemático. Un abordaje hermenéutico desde el escenario de
la educación inicial
Didactics and development of mathematical logical thinking. A hermeneutical approach from the initial education stage
Didática e desenvolvimento do pensamento lógico matemático. Uma abordagem hermenêutica a partir do cenário da educação inicial
Jelly Katherine Lugo Bustillosa* | Overlys Vilchez Hurtadob | Luis Jesús Romero Álvarezc
a http://orcid.org/0000-0002-0108-3771
b http://orcid.org/0000-0003-3149-4851
c http://orcid.org/0000-0003-1998-353X
Núcleo de Investigación Educativa Paraguaná, Venezuela
Resumen
El objetivo de este estudio tiene como finalidad explorar la práctica docente en el desarrollo del pensamiento lógico matemático de los niños de un centro de educación inicial de Paraguaná, Venezuela. El paradigma es cualitativo con un diseño de estudio de caso, modalidad de campo, de tipo interpretativo
apoyado en el método hermenéutico-dialéctico. Se utilizó como técnica la entrevista en profundidad mediante un guion de entrevista semiestructurado contentivo de 3 subtemas a explorar con 14
preguntas abiertas dirigidas a 6 docentes. Se procesó la información obtenida a través del software Atlas Ti 6.0, se codificó, categorizó, y se crearon redes semánticas, que facilitaron la interpretación de los hallazgos, los cuales reflejan que la mayoría de los docentes poseen poco conocimiento sobre los procesos del pensamiento lógico matemático y, por ende, aplican estrategias de enseñanza monótonas y descontextualizadas donde la instrucción se prioriza ante la mediación docente.
Palabras clave: educación inicial, pensamiento lógico matemático, enseñanza monótona, descontextualizadas, mediación docente
Summary
The objective of this study is to explore the teaching practice in the development of mathematical logical thinking in children from an early education center in Paraguaná, Venezuela. The paradigm is qualitative with a case study design, an interpretive field component supported by the hermeneutic-dialectical method. An in-depth interview was used as a technique through a semi-structured interview script containing 3 sub-topics to be explored with 14 open questions addressed to 6 teachers. The information obtained through the Atlas Ti 6.0 software was processed, codified, categorized, and semantic networks were created, facilitating the interpretation of the findings, which show that most teachers have little knowledge about the processes of mathematical logical thinking and, therefore, apply monotonous and decontextualized teaching strategies where instruction is prioritized over teacher mediation.
Keywords: early education, mathematical logical thinking, monotonous teaching, decontextualized, teaching mediation
Sumário
O objetivo deste estudo é explorar a prática docente no desenvolvimento do pensamento lógico matemático das crianças de um centro de educação inicial de Paraguaná, Venezuela. O paradigma é qualitativo com um projeto de estudo de caso, modalidade de campo, de tipo interpretativo apoiado no método hermenêutico-dialético. Utilizou-se como técnica a entrevista em profundidade mediante uma roteiro de entrevista semiestruturado que contem 3 subtemas a explorar com 14 perguntas abertas dirigidas a 6 docentes. A informação obtida foi processada através do software Atlas TI 6.0, foi codificada, categorizada, e foram criadas redes semânticas, que facilitaram a interpretação dos achados, os quais refletem que a maioria dos docentes possui pouco conhecimento sobre os processos do pensamento lógico matemático e, portanto, aplicam estratégias de ensino monótonas e descontextualizadas onde a instrução é priorizada diante da mediação docente.
Palavras-chave: educação inicial, pensamento lógico matemático, ensino monótono, descontextualizados, mediação docente
En el proceso de aprendizaje, los conceptos lógico matemáticos constituyen un instrumento fundamental y útil, porque a través de estos los niños expresan cada día sus conocimientos en cada una de las experiencias de formación educativa. En este conglomerado de experiencias de formación, la familia, así como los docentes, son también protagonistas, en virtud de que deben trabajar en conjunto para la búsqueda y aplicación de las más eficientes estrategias didácticas que ayuden al niño a entender todo lo que observa.
Podemos decir, entonces, que el niño, en su proceso de construcción de conocimiento, establece contacto con situaciones y objetos que le permiten desarrollar su pensamiento lógico, clasificando las relaciones sencillas que anteriormente ha creado entre los objetos (Balmaceda, 2017). En este sentido, debe destacarse que los conocimientos o habilidades en esta área tienen gran valor para el ser humano, porque, además de contar objetos, el individuo desarrolla su capacidad para razonar y reflexionar sobre cualquier situación de su interés. Siendo así, amerita que tanto padres como maestros se conviertan en creativos para aplicar estrategias didácticas que apoyen el desarrollo de este pensamiento desde temprana edad.
De acuerdo con lo anterior, en los contextos escolares recae un compromiso indelegable para propiciar los escenarios cargados de estrategias para desarrollar el pensamiento lógico matemático, exigiendo de esta manera docentes capacitados en el dominio de nociones básicas que le permitan diseñar las estrategias pertinentes para potenciar estos aprendizajes (Intriago, Giler, Meza, Sacoto & Meza). Al hablar de escolaridad, es necesario puntualizar la importancia que tiene hacer seguimiento de estos aprendizajes desde la etapa preescolar. Para efectos de este estudio, el análisis se orienta a identificar la realidad del Centro de Educación Inicial “Simón Bolívar” del municipio Carirubana del estado Falcón, Venezuela.
Para ello, es necesario mencionar lo que sustenta el currículo de educación inicial venezolano (2007), cuando plantea que el niño, en la evolución de su aprendizaje debe lograr la construcción de sus conocimientos por medio de la descripción de códigos lingüísticos, asimismo
matemáticos, científicos y sociales. Del mismo modo, debe lograr establecer comparaciones de causa-efecto en el contexto donde se desenvuelve, aplicando en su proceso de conocimiento, experiencias y desarrollar un pensamiento crítico, que le sea de ayuda para la búsqueda de soluciones en las diversas situaciones y problemas que se le presenten en su vida diaria.
Tomando como punto de referencia lo anterior, es menester destacar que en el Centro de Educación Inicial “Simón Bolívar”, en lo relacionado con los ambientes de aprendizajes, destaca cierta situación en cuanto al uso de los materiales didácticos del espacio de armar y construir, pudiéndose decir que los niños no le dan el uso adecuado; lo que pudiera estar dado por debilidades en la mediación docente, constituyendo esto, sin duda, alguna afronta al desarrollo efectivo de los procesos de enseñanza y aprendizaje.
Todo docente debe manejar un conocimiento exhaustivo sobre el desarrollo evolutivo del niño y la niña, de lo contrario, representaría serias debilidades para la práctica pedagógica en los centros educativos, entre las que destaca la imposibilidad del docente respecto a cómo ubicar al niño(a) en una etapa evolutiva que le corresponde y, por ende, el declive en la producción y ejecución de estrategias tanto para el pensamiento lógico matemático como para las demás áreas del aprendizaje.
Desde este escenario, y considerando el papel determinante del docente en la planificación, ejecución, evaluación y mediación, así como en el uso de estrategias, materiales didácticos y los demás procesos inherentes a la educación, es necesario reflexionar sobre lo que plasma el Currículo Bolivariano de Educación Inicial (2007), cuando indica:
[…] el docente es un profesional que está consciente de su vocación para el ejercicio de la docencia, congruente
en su sentir, pensar y actuar; con altos niveles de conciencia y responsabilidad, tanto de sí mismo y sí misma como de la realidad física y social donde se encuentra (p. 17).
De allí que, según lo que se observa de la realidad que se vive en este centro educativo, hay una aparente pasividad en gran parte de los docentes al momento de desarrollar estrategias pedagógicas, sobre todo las dirigidas a potenciar el pensamiento lógico matemático en los niños, así como también cierta resistencia a algunos cambios para acoplarse a los nuevos paradigmas relacionados con la innovación en los procesos de enseñanza y aprendizaje.
Referentes teóricos sobre el desarrollo de los procesos lógico matemáticos en educación inicial
Piaget (1975) plantea que “el proceso lógico matemático se enfatiza en la construcción de la noción del conocimiento, que se desglosa de las relaciones entre los objetos y desciende de la propia producción del individuo” (p. 20); es decir, el niño construye el conocimiento lógico matemático, coordinando las relaciones simples que previamente ha creado entre los objetos, lo cual, viéndolo desde este punto de vista, exige que el docente sea conocedor de todos los aspectos relacionados con dicho tema para orientar y potenciar estos procesos en los niños y así lograr la consolidación de un aprendizaje significativo, integrador, autónomo, comprensivo.
Al respecto, Ausubel (1998) plantea una idea interesante cuando afirma que “el aprendizaje se basa en la restructuración activa de los procesos mentales que se suscitan en la estructura cognitiva del ser humano” (p. 123). Esto implica que la interacción entre la información, sus conocimientos previos, y las características personales del individuo, hacen que su aprendizaje sea autónomo, y mantenga una relación con sus objetos y el medio en que se desenvuelve.
Cabe destacar que Vygotsky y Souberman (1978), en su teoría sociocultural a raíz del aprendizaje significativo, sustentan “que todo aprendizaje escolar tiene su historia previa. Por tanto, el niño en su interacción con el entorno ha construido en forma ‘natural’ nociones y estructuras cognitivas que continúan desarrollándose mediante la enseñanza escolarizada” (p. 21).
Estos autores se refieren con esto, que el maestro en su práctica pedagógica no está constituido sobre la base de los conocimientos naturales del niño y la niña. En su mayoría los orienta hacia la ejecución temprana del cálculo. Por ello, el estudio de esta investigación para explorar sobre su práctica, estas acciones del educador hacia el educando, arroja que el docente desconoce las etapas o fase del proceso cognitivo de cada niño.
Es por ello por lo que Vygotsky y Souberman (1978) definen la Zona de Desarrollo Próximo, como:
[…] la distancia que hay entre el nivel real de desarrollo determinado por la solución independiente de problemas y el nivel de desarrollo posible, precisado mediante la solución de problemas con la dirección de un adulto o colaboración de otros más diestros (p. 2).
Siendo más explícito con la definición, mediante estrategias y herramientas suministradas, y el maestro como mediador o modelo de esa enseñanza y aprendizaje a impartir, esto incide en el niño de manera positiva, porque a través de esta, él puede llegar al desarrollo independiente de sus actividades, o la búsqueda de la solución de algún problema, del mismo modo la cooperación abierta de
alguna actividad pedagógica (López, 2018).
Relacionando lo dicho por Piaget (1975) con el desarrollo del pensamiento lógico matemático, puede decirse que el conjunto de experiencias van a permitir la estructuración de este pensamiento en el niño desde tempranas edades, y que, sin duda alguna, las condiciones de los escenarios y la participación de los actores del proceso de enseñanza y aprendizaje en estos aspectos conjugarán una tarea fundamental en el desarrollo y consolidación de este pensamiento en las diferentes etapas de su desarrollo.
En este orden de ideas, resulta apropiado mencionar algunas impresiones que expresa Morales (2017) en un estudio relacionado con el conocimiento que poseen los docentes acerca del desarrollo del pensamiento lógico matemáticos en el niño, cuando afirma que el docente forma parte precisamente del conjunto de actores que intervienen en el desarrollo de este pensamiento cuando el niño ya es escolarizado, y que deberá entonces considerar las experiencias que traen consigo los estudiantes; además de mantener una actitud crítica frente a la selección de las formas de enseñanza y las estrategias que, según el que sugiere el autor, deben ser creativas y motivadoras del aprendizaje.
Continúa aportando el autor precitado, que para desarrollar este pensamiento matemático en los niños de los primeros niveles educativos, el docente debe tener una formación que le permita ser capaz de comprender las formas de enseñar estos contenidos ajustándose a la edad del niño, y apropiándose de la curiosidad innata característica de estas edades para así robustecer sus estrategias de enseñanza y aprendizaje (Morales, 2017). Y en relación con esta última idea, Morales afirma que por años el estilo de formación que se ha dado para la etapa de educación inicial ha sido meramente asistencial, de manera que no solo se requiere preparar a los niños con lectura y escritura para su escolarización, sino que también existen otros procesos que deben desarrollarse en el niño y que necesariamente exigen de la preparación del docente para asumir una mediación efectiva.
Es así como la mediación de aprendizajes tiene un papel fundamental y debe posicionarse en la comprensión y la significación de esos conceptos a desarrollar. El compromiso pedagógico debe estar encaminado en exaltar la interacción del niño(a) con los objetos del ambiente para obtener un aprendizaje significativo, integrador, compenetrado y autónomo. La experiencia del educador debe partir siempre de lo que el niño(a) posee y conoce, con respecto a lo que se pretende que aprendan. Solo desde esa base pueden enlazarse los nuevos conocimientos con sus potencialidades e intereses para ampliar de esa manera todos sus esquemas perceptivos y su capacidad de razonamiento (Lima & Ramírez, 2018).
Desde esta perspectiva, a interacción del niño con el medio es el escenario ideal para propiciar las experiencias que generen aprendizajes verdaderamente significativos, y con esta dinámica, los recursos materiales con los que tiene contacto el niño, juega un papel determinante, aún más el provecho que pueda extraer el docente para generar conflictos cognitivos que conlleven reflexiones y desarrollo del pensamiento lógico en los estudiantes. Cruz y Quispe (2017) al respecto afirman que los recursos que se tornan en materiales didácticos sirven como un valioso medio no solo para motivar, sino también para reforzar aprendizajes en la medida que sean utilizados eficientemente para el desarrollo de actividades escolares, como medios de consulta del docente o como apoyo para el trabajo de diversos contenidos en diferentes escenarios sociales. En este sentido, los autores consideran que cada recurso didáctico varía de utilidad, según las características propias del objeto y el propósito de quien lo ha diseñado.
Tal situación exige al docente asumir de forma diligente y con esmero, múltiples retos para brindar las herramientas y recursos adecuados para así desarrollar competencias en el niño(a), según lo que sustenta el Diseño Curricular de Educación Inicial (2005).
Volviendo a lo observado en la realidad del Centro de Educación Inicial que conforma el contexto de este estudio, se puede decir que pareciese que las situaciones de aprendizaje que promueve el maestro se fundamenta en la introducción del signo numérico sin referencia a su significado, manejándose como enunciados en forma mecánica, y prevaleciendo su escritura en hojas multigrafiadas. Caso similar ocurre en cuanto a los espacios de
aprendizajes donde deben existir la mayor cantidad
de materiales didácticos para desarrollar este tipo de pensamiento, los cuales presentan carencias en la dotación de estos recursos didácticos para trabajar con las nociones lógico matemáticas.
Además, los niños al usar recursos como tacos, legos y otros relacionados al desarrollo de procesos lógicos matemáticos, no es lo más adecuado, ya que estos le asignan otras funciones a los mismos, dando muestra entonces de que pudiesen existir debilidades en la mediación docente para el uso efectivo de estos recursos, lo cual pudiere estar afectando en gran parte su enseñanza y aprendizaje.
Método
El objetivo de esta investigación tiene como fin explorar la práctica docente dirigida al desarrollo del pensamiento lógico matemático de los niños de un centro de educación inicial de Paraguaná, Venezuela. El estudio se basó en el paradigma cualitativo, con un diseño de estudio de caso, ya que se realizó el abordaje bajo la modalidad de campo directamente en el contexto del Centro de Educación Inicial “Simón Bolívar” de la localidad venezolana previamente señalada.
Desde el enfoque cualitativo, nos apegamos al método hermenéutico dialéctico para comprender los diversos significados interrelacionados en las expresiones de los docentes que formaron parte de las unidades de análisis. En este orden de ideas, se aplicó la técnica de la entrevista con la utilización de un guion semiestructurado contentivo de 14 preguntas abiertas, para tres subtemas a explorar que buscaban ahondar; en primer lugar, en las nociones del proceso lógico matemático, que poseen los docentes, así como las estrategias didácticas que aplican para el desarrollo del pensamiento lógico matemático en los niños y, por último, los recursos y ambiente de
aprendizajes que caracterizan el desarrollo de estas prácticas educativas.
Los informantes claves fueron seis docentes que laboran en la institución educativa ya mencionada, quienes cubren la atención pedagógica de los niños en los turnos matutino y vespertino. Puede mencionarse que los informantes son de amplia trayectoria en el ámbito de la atención en el nivel de educación inicial.
Las entrevistas se realizaron en un clima armónico y bajo el consentimiento informado de la totalidad de docentes de la institución educativa, durante el periodo de 12 días (entre el 14 y 25 de enero de 2019). La información
recogida se procesó posteriormente con el apoyo del software Atlas Ti 6.0, que constituye una de las herramientas digitales utilizadas para el procesamiento de información en investigaciones cualitativas, gracias a las ventajas que ofrece para organizar la información de manera gráfica, mediante la construcción de redes semánticas donde confluyen las relaciones establecidas entre los códigos con múltiples significados atribuidos por los informantes a cada una de las dimensiones, subtemas o categorías estudiadas. Finalmente, la discusión de los significados de los códigos y las relaciones establecidas, constituyen los hallazgos de esta investigación.
Hallazgos: discusión y valoración de la praxis
El procesamiento de la información permitió crear 38 códigos (véase tabla 1), que responden a las tres categorías o subtemas indagados: (a) nociones del proceso lógico matemático, (b) estrategias didácticas para el desarrollo del pensamiento lógico matemático y (c) recursos y ambientes para el aprendizaje.
Los códigos de la tabla 1 se organizaron y se muestran en redes semánticas que responden, como ya se dijo, a los subtemas explorados: (a) nociones del proceso lógico matemático, (b) estrategias didácticas para el desarrollo del pensamiento lógico matemático y (c) recursos y
ambientes para el aprendizaje, y cuya organización gráfica en forma de redes semánticas, parte de la codificación abierta donde se establece la relación entre códigos para la que se utilizó la leyenda que se muestra en la tabla 2, lo cual facilita la interpretación de la información sobre la práctica docente en el desarrollo del pensamiento lógico matemático de los niños del Centro de Educación Inicial “Simón Bolívar”.
Tabla 1. Listado general de códigos extraídos de las entrevistas
|
Codigos |
|
|
1. |
Ambiente |
|
2. |
Aprendizaje |
|
3. |
Asociación |
|
4. |
Clasificación |
|
5. |
Componentes |
|
6. |
Conocimientos |
|
7. |
Construcción |
|
8. |
Creatividad |
|
9. |
Diagnóstico |
|
10. |
Disposición |
|
11. |
Diversidad de material |
|
12. |
Dotación |
|
13. |
Enseñanzas |
|
14. |
Espacios |
|
15. |
Estrategias |
|
16. |
Evaluación |
|
17. |
Etapa o fase |
|
18. |
Experimentación |
|
19. |
Falta de recurso |
|
20. |
Formación |
|
21. |
Guía de indicadores |
|
22. |
Incumplimiento de planificación |
|
23. |
Innovación |
|
24. |
Instrucción |
|
25. |
Intereses |
|
26. |
Juegos |
|
27. |
Matemático |
|
28. |
Motivación |
|
29. |
Material didáctico |
|
30. |
Necesidades |
|
31. |
Observación |
|
32. |
Proceso lógico matemático |
|
33. |
Planificación |
|
34. |
Poco conocimiento |
|
35. |
Potenciar |
|
36. |
Proceso |
|
37. |
Razonamiento |
|
38. |
Recurso |
Fuente: Lugo, Vílchez y Romero (2019).
Tabla 2. Relaciones para la codificación abierta
|
ASSO |
= = |
“está asociado a” |
|
BPT |
[ ] |
“es parte de” |
|
CAUSA |
= |
“es causa de” |
|
ISA |
Isa |
“es de” |
|
PROP |
*} |
“pertenece a” |
Fuente: software Atlas Ti 6.0.
Como puede apreciarse en la tabla 2, se ha asignado un símbolo para cada relación establecida entre códigos. Estas relaciones podrán verse en las redes semánticas construidas por cada dimensión estudiada, las cuales se irán presentando progresivamente en las siguientes líneas acompañadas de la discusión de los hallazgos obtenidos.
a) Nociones del proceso lógico matemático
En esta dimensión o subtema, se muestran las nociones que manejan los docentes con relación al pensamiento lógico matemático, su fundamentación en el currículo de educación inicial, los diversos procesos que se desarrollan en el pensamiento lógico matemático, el dominio que manifiestan los docentes en la estimulación de alguno de los componentes del proceso lógico matemático y sus impresiones sobre cómo puede abordarse la enseñanza del proceso lógico matemático en los niños.
De acuerdo con las respuestas obtenidas por los informantes claves en esta red, se generaron 17 códigos que posteriormente se interrelacionaron (véase figura 1). Los informantes expresan que el pensamiento lógico matemático lo componen las capacidades en cuanto a clasificar, ordenar objetos, asimismo elementos del entorno y cantidades numéricas. Otro docente manifiesta que este tipo de pensamiento es la concepción que va adquiriendo el niño del espacio, cantidades y formas, lo que deja ver que existe quizá marcada influencia entre la formación inicial o universitaria del docente y sus concepciones respecto a este tema.
Como se observa en la red semántica de la figura 1, las relaciones suscitadas entre los diferentes códigos revelan también que, según los informantes, el proceso lógico matemático está ubicado en el área de aprendizaje en relación con el ambiente, del currículo de educación inicial. De la misma manera, otro docente expresaba la misma respuesta, pero haciendo énfasis en que tiene que ver con todo el entorno donde se desenvuelve el niño que ofrece las oportunidades ideales para trabajar todo lo relacionado con números y otros conceptos asociados.
Cabe señalar que los informantes en sus respuestas consideran que la enseñanza o desarrollo de este estilo de pensamiento debe realizarse por medio del juego, ya que manifiestan que a través de la lúdica el niño(a) puede seguir cualquier instrucción que le dirija a un nuevo aprendizaje. Así también lo reflejaba otro docente, quien planteaba que para el niño(a) el seguimiento de una instrucción es parte primordial de la construcción de su conocimiento, puesto que lo ayuda al desarrollo de su pensamiento lógico matemático, que es abordado desde el inicio de la etapa o fase maternal hasta que ingresa al proceso educativo (escolar).
En este orden de ideas, y en palabras de docentes entrevistados, se deja ver que entienden por proceso lógico matemático aquel donde se desarrolla exclusivamente conceptos numéricos, así como la seriación, conteo y clasificación, lo que les permite a los niños la capacidad de razonamiento (véase tabla 3). De igual manera, exponen que puede abordarse a través de diferentes estrategias, como la incorporación de actividades donde el niño clasifique a través del color, forma, conteo de objetos, entre otras estrategias donde apliquen la innovación, la cual sea la motivación el eje primordial tanto para el docente como para el niño o la niña.
Las expresiones de los docentes entrevistados permiten tener insumos suficientes para considerar que la noción docente respecto al proceso lógico matemático se circunscribe a conceptos numéricos, de agrupación, clasificación, figuras geométricas y algunas nociones espaciales. Al respecto, estos hallazgos no resultan muy diferentes a los obtenidos en el estudio de Morales (2017), que revelan que los docentes poseen un bajo conocimiento profesional
sobre los aspectos relacionados al pensamiento matemático de los niños de edad infantil y que, por ende, estas debilidades inciden de forma negativa en el resto de los momentos que intervienen en los procesos de enseñanza y aprendizaje, como lo es la selección de estrategias, ambientes de aprendizaje o recursos didácticos, solo por mencionar algunos.
b) Estrategias didácticas para el desarrollo del
pensamiento lógico matemático
Esta categoría contempla la información relacionada
sobre cómo los docentes aplican sus estrategias para desarrollar el pensamiento lógico matemático; para ello, se presenta una red semántica con la construcción de 26 códigos compuestos de la narrativa de los informantes (véase figura 2).
Cabe resaltar que los docentes entrevistados señalan que en todo momento de la rutina diaria utilizan estrategias para promover el desarrollo del pensamiento lógico matemático en los niños, mediante situaciones de aprendizaje que implican pedirle que realicen una formación y que los niños se ubiquen detrás de o delante de, o cuando los
envían a la mesa y manejan cantidades y espacio. Consideran que por medio de este tipo de estrategias implementan
la observación, según la planificación que se esté abordando y que los procesos de enseñanza y aprendizaje se dejan como estrategia para utilizar.
Por su parte, otro docente expone que según las situaciones de aprendizaje en particular no es ninguna, los niños siempre prefieren el juego en el espacio de armar y construir, siendo este uno de los espacios que cuenta con material didáctico que pudiese aplicar estrategias como el conteo de tacos, clasificación de objetos por tamaño, color, grosor, entre otras. Por ende, se evidencia la apatía del docente en darle el uso adecuado al material didáctico que posee en este espacio. Mientras otro informante divulga que con las actividades multigrafiadas con números para transcribir es la forma de la cual desarrolla el proceso lógico matemático.
Por consiguiente, otro docente revela que depende del tipo de planificación que se esté abordando, según el interés o necesidades del niño(a), que se da la aplicación de la estrategia en función de fomentar esto en los estudiantes con objeto de que ellos avancen al siguiente nivel de aprendizaje, y para ello pueden aplicarse dinámicas grupales, según la diversidad de material que maneje, así como también actividades lúdicas, entre otras. En palabras de los informantes, se afirma que es necesario ver los aspectos que deben tomarse en cuenta para seleccionar la estrategia adecuada para el desarrollo del pensamiento lógico matemático, que exprese el interés de los niños, sus necesidades y conocimiento, porque es importante tomar en consideración el potencial que poseen para trabajar colaborativamente y reforzar los aprendizajes de otros niños(as).
Así también, otro informante opinó que, en el diseño de estrategias didácticas, parte de la observación a la conducta del niño(a) para ver el nivel de aprendizaje en el que se encuentra; ya que no puede colocar actividades con alto nivel de complejidad que como docente sabe que ellos no pueden realizar. En segundo lugar, considera la aplicación de estrategias pedagógicas enmarcadas en la innovación y dinámicas que los impulse con motivación a aprender lo que se les quiere enseñar (véase tabla 4).
Como se observa en las expresiones anteriores, también los docentes manifiestan tener debilidades en el desarrollo de su práctica docente para potenciar estos procesos en el niño o en la niña y lo atribuyen a la falta de recursos didácticos; sin embargo, expresan que con el poco recurso que tienen a su alcance, buscan dar lo mejor para que el niño(a) adquiera ese aprendizaje. De igual forma, es preocupación para otra parte de los informantes el hecho de que consideran que tienen poco conocimiento sobre los niveles de aprendizaje pautados en la guía de indicadores; por lo cual creen necesaria una continua formación para el fortalecimiento de sus conocimientos. Tales debilidades inciden de manera significativa en el incumplimiento de la planificación del día pautado, según los informantes.
Testimonio único y contrario fue el de un docente, que manifestó tener la ventaja de llevar a cabo estrategias que brinden al niño(a) la experimentación con diferentes objetos, permitiéndole comparar, clasificar, seriar, entre otras. Igualmente, plantea que la observación que realizaba al grupo de niños(as) le arrojaba un diagnóstico que le serviría para fortalecer alguna debilidad presentada en su proceso.
Ante tales hallazgos, es claro que los informantes tienen conciencia de que ellos presentan serias debilidades en el abordaje de estrategias didácticas para promover los aprendizajes en esta área; lo que, sin duda, hace que las actividades sean monótonas y circunscritas a actividades dentro del aula, y reconocen que esta cuenta con pocos recursos para estimular el pensamiento lógico matemático en los niños.
En este sentido, López (2018) plantea la importancia de la incorporación de estrategias vivenciales como medio alterno de construcción de aprendizajes y como medida creativa para sobreponerse a las debilidades típicas que presentan muchos contextos escolares en cuanto a la incorporación de materiales didácticos dentro del aula. Así pues, es un reto para los docentes, idearse las nuevas formas de enseñanza y desarrollo de estos aprendizajes, que se logrará, según el autor precitado, con un serio compromiso con la acción educativa, una capacitación constante y un abordaje consciente de su acción docente para el aprovechamiento creativo de los recursos y materiales con los que dispone en los contextos naturales de interacción social de los niños a su cargo.
c) Recursos y ambientes para el aprendizaje
Esta categoría se enfoca en presentar los recursos utilizados en los ambientes de aprendizajes para la ampliación de nuevos conocimientos dados en todo momento de la rutina diaria, en su espacio de aprendizaje. Se resalta que el recurso es todo lo que acompaña a la ejecución de una estrategia, tales como dibujos, canciones, juegos, material didáctico, entre otros.
Según el estudio que se viene abordando y atendiendo a las opiniones de los docentes entrevistados, cuando se les preguntaba sobre los recursos que poseen dentro de los ambientes de aprendizaje para estimular el desarrollo del pensamiento lógico matemático de los niños y las niñas, estos expresaron que en sus ambientes de aprendizajes, existen recursos didácticos, como tacos, legos (forma, color, tamaño, grosor), juego de memorias (animales), cestas con diversos materiales (colores, pintura, material escolar), que es de gran apoyo para la ejecución de la enseñanza de acuerdo con múltiples procesos. Del mismo modo, otro informante indicaba que dentro de su ambiente de aprendizaje se nota una marcada ausencia de materiales didácticos que no favorece al fortalecimiento del pensamiento lógico matemático en el niño(a) (véase figura 3).
Por otro lado, se indagó sobre los tipos de ambiente que utilizan para desarrollar estrategias en el pensamiento lógico matemático, ante lo cual los informantes expresaron que todos los espacios del ámbito educativo son ideales para desarrollar nociones lógico matemáticas en los niños. Un docente de forma explícita indicaba que solo es posible que se consolide este aprendizaje si realmente se promueve mediante actividades planificadas, aplicando estrategias didácticas por medio del juego en el espacio de armar y construir, actividades pedagógicas en el espacio de expresar y crear.
Se entiende, entonces, que la mediación que ejerce el maestro tiene un papel fundamental, cuando se hace uso del recurso; y en este sentido, existen muchas otras estrategias que aplican los docentes para enseñar, o lograr la integración del grupo sin necesidad de aplicar un material didáctico; que pudiera ser aprovechando cada momento y abordando estos conceptos desde el momento de la bienvenida a través de las nociones espaciales para ubicar a los niños(as) delante de, detrás de, por ejemplo.
Vale acotar que hubo una pregunta que invitó a los entrevistados a razonar sobre cómo obtendría el niño(a) un aprendizaje significativo a través de la manipulación de los recursos o materiales didácticos existentes en su
ambiente de aprendizaje. Uno de ellos expresaba que por medio de materiales encontrados en deterioro y con ayuda de los mismos niños(as), iban recuperándolos y, a su vez, dándoles el uso adecuado para ir adquiriendo esos conocimientos. Otros planteaban que lo hacían mediante el modelaje y la interacción que el docente le brinda al niño, o la mediación que desempeña un papel fundamental, sin dejar de pronunciar que al ejecutar la planificación debe haber una dotación en los espacios y saber manejar el recurso.
En cuanto a las acciones que aplica el docente para emprender el pensamiento lógico matemático, se considera que debe partir de utilizar de forma combinada sus recursos, para promover los procesos relacionados con la reversibilidad; de igual forma, las nociones de clasificación, seriación, correspondencia uno a uno, entre otras.
Con respecto al desarrollo de estas actividades por parte del maestro, si este no maneja su recurso de manera adecuada y no posee una reflexión teórica, se evidenciará la carencia de la finalidad específica dentro del hacer didáctico. Es decir, que el docente no posee una instrucción didáctica referente a las actividades que promueve dentro de su espacio o ambiente de aprendizaje, esto evoca que la formación del educador en este nivel educativo es
endeble (véase tabla 5).
Los hallazgos en esta categoría revelan parte de las consecuencias de una formación docente con debilidades en cuanto al conocimiento sobre el desarrollo del pensamiento lógico matemático de los niños en edad preescolar y las estrategias didácticas para abordarlo. Los docentes en su mayoría, reconocen de forma teórica la importancia de la incorporación de los recursos didácticos efectivos para esta área y la importancia de su mediación docente; pero en la praxis emergen ciertas debilidades que se resumen en actividades y uso de recursos poco llamativos y motivadores, o en el peor de los escenarios, un mal uso de un buen recurso didáctico.
Es así como Carrera (2017) concluía en su investigación, que la mayoría de los docentes son víctimas del desconocimiento o de una formación docente pírrica, que se refleja en la carencia de recursos didácticos en sus planificaciones o en sus actividades pedagógicas, porque no dominan con certeza las nociones necesarias para organizar los procesos de enseñanza y aprendizaje en las diversas áreas, especialmente en los contenidos relacionados con las matemáticas y los procesos lógicos del pensamiento que, a su parecer, requieren de una formación docente especializada para comprender cabalmente los procesos cognitivos por los que transcurre la madurez del niño, su relación con esta área y las formas como mediar para potenciar estos aprendizajes.
Conclusiones
Del ejercicio comprensivo de los significados atribuidos por los docentes al desarrollo del pensamiento lógico matemático en los niños en edad preescolar, se concluye que los docentes manejan una noción reduccionista de procesos lógicos matemáticos y su desarrollo en edad escolar, enmarcándolo en procesos como numeración, seriación, conteo y clasificación.
En este sentido, aunque los docentes le atribuyen un gran valor a la ejecución de una observación sistemática a los procesos cognitivos de los niños, la motivación, el juego y la innovación para el desarrollo del pensamiento lógico matemático en los niños, en la práctica todo se resume a la realización de actividades con legos, tacos, conteo, dibujos y escritura de números que resultan monótonas y poco efectivas para desarrollar de manera eficiente el pensamiento lógico y las nociones matemáticas desde tempranas edades.
Los docentes conservan una actitud crítica al reconocer que muchas de las interferencias que presentan para el abordaje de estos contenidos se debe a la escasez de recursos materiales para ejercer una mediación efectiva, y a las serias debilidades en cuanto a su formación inicial o profesional en esta área. Queda mucho por hacer entonces en cuanto a la formación docente continua y especializada en estas temáticas para que realmente se pueda encaminar un proceso de organización, potenciación de aprendizajes efectivo, específicamente en lo que respecta al
desarrollo de estas nociones lógico matemáticas en la primera infancia. Sin lugar a dudas, de una capacitación docente de calidad, aunada a la voluntad y creatividad, dependerá mucho del éxito que se obtenga en las prácticas docentes dirigidas a los fines hasta ahora discutidos.
Referencias
Ausubel, D., Novak, J., & Hanesian, H. (1998). Psicología educativa, un punto de vista cognoscitivo. Primera edición en español (1983). México: Editorial Trillas. Decimoprimera reimpresión.
Balmaceda-Vásquez, T. D. C. (2017). Estrategia metodológica que utiliza la docente en el desarrollo lógico matemático para sus alumnos de multinivel de educación inicial en el colegio público Esther Galiardys de ciudad Sandino en el segundo semestre del año 2016 (tesis doctoral). Managua, Nicaragua: Universidad Nacional Autónoma de Nicaragua. Recuperado de http://repositorio.unan.edu.ni/id/eprint/3802.
Carrera-Cargua, A. (2017). Uso de materiales didácticos en el proceso de enseñanza-aprendizaje en el ámbito lógico matemático de los niños/as de educación inicial (tesis doctoral). Ecuador: PUCESE, Maestría en Ciencias de la Educación. Recuperado de https://repositorio.pucese.edu.ec/handle/123456789/1087.
Cruz-Saravia, R. E., & Quispe-Arroyo, N. M. (2017). El material lúdico en el desarrollo de las capacidades del área de matemática en los niños y niñas de 4 años de educación inicial. Recuperado de http://repositorio.unh.edu.pe/handle/UNH/1489.
Intriago, H. A. M., Giler, A. D. A., Meza, N. N. L., Sacoto, J. H. C., & Meza, E. P. L. (2017). Desarrollo del pensamiento lógico matemático, mediación y aprestamiento en la educación inicial. Revista Científica Multidisciplinaria, 1(3), 81-88. Unesum-Ciencias. Recuperado de http://www.refcale.uleam.edu.ec/index.php/unesumciencias/article/view/2919.
Lima-Chica, F. N., & Ramírez-Borbor, M. A. (2018). Estrategias metodológicas en la iniciación del pensamiento lógico matemático en niños de educación inicial (tesis de licenciatura). Recuperado de http://repositorio.unemi.edu.ec/handle/123456789/4145.
López-Huamán, T. N. (2018). Estrategias para favorecer el desarrollo lógico matemático en niños del II ciclo de educación inicial. Recuperado de http://repositorio.une.edu.pe/handle/UNE/3002.
Ministerio de Educación y Deportes. (2005). Educación inicial. Básicos curriculares. Caracas: Torino.
Ministerio del Poder Popular para la Educación. (2007). Diseño curricular del sistema educativo bolivariano. Caracas: autor.
Morales-Parrales, P. M. (2017). Conocimiento del contenido matemático infantil en docentes de educación inicial, circuito educacional No. 2, Esmeraldas (tesis doctoral). Ecuador: PUCESE, Escuela Ciencias de la Educación-Educación Inicial). Recuperado de https://repositorio.pucese.edu.ec/handle/123456789/1281.
Piaget, J. (1975). El desarrollo del pensamiento. Buenos Aires: Paidós.
Vygotsky, L. S., & Souberman, E. (2012). El desarrollo de los procesos psicológicos superiores (No. 159.92 VYG).
http://dx.doi.org/10.22335/rlct.v11i3.991

* Autor para correspondencia. Correo electrónico: jklb83@gmail.com
Para citar este artículo / To reference this article / Para citar este artigo: Lugo, J. K., Vilchez, O., & Romero, L. J. (2019). Didáctica y desarrollo del pensamiento lógico matemático. Un abordaje hermenéutico desde el escenario de la educación inicial. Revista Logos Ciencia & Tecnología, 11(3), 18-29. http://dx.doi.org/10.22335/rlct.v11i3.991
Revista Logos, Ciencia & Tecnología
ISSN 2145-549X (impreso)
ISSN 2422-4200 (en línea)
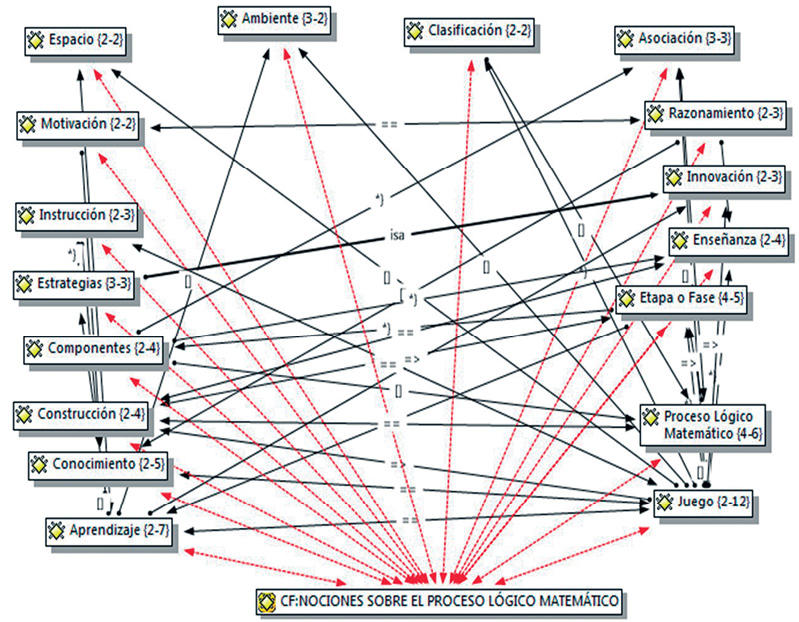
Figura 1. Red semántica: nociones sobre el pensamiento lógico matemático
Tabla 3. Expresiones sobre las nociones del proceso lógico matemático
|
Informante |
Unidad de análisis |
|
1 |
“El proceso lógico matemático se aborda desde el inicio de la etapa escolar desde que el niño(a) ingresa al proceso educativo (maternal)”. |
|
2 |
“Es la concepción que va adquiriendo el niño de espacio, cantidades y formas”. |
|
3 |
“Las nociones del proceso lógico matemático es para que los niños aprendan, los números, conteo por cantidades, por medio de símbolo o signos”. |
|
4 |
… “es el proceso de donde se desarrolla la parte numérica, la seriación, conteo, agrupar, clasificar, esto le permitirá a los niños la capacidad de razonar”. |
|
5 |
… “no es más que todo lo concerniente a la formación, preparación y noción de números, figuras geométricas, noción espacial y temporal”. |
|
6 |
… “se concibe como la iniciación de adquisición de números, capacidades, formas, tiempo, espacios y longitud, en el área de preescolar”. |
Fuente: información suministrada por los entrevistados.
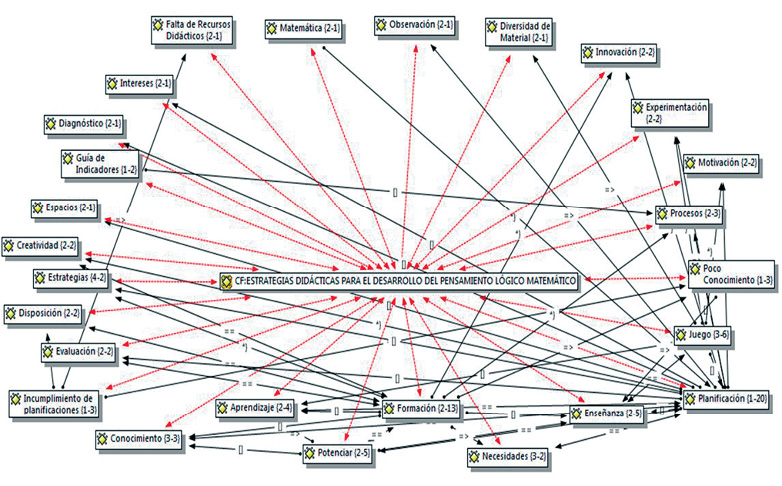
Figura 2. Red semántica: estrategias didácticas para el desarrollo del pensamiento lógico matemático
Tabla 4. Expresiones sobre las estrategias didácticas para el desarrollo del pensamiento lógico matemático
|
Informante |
Unidad de análisis |
|
1 |
… “Primeramente, tomando en cuenta los intereses de los niños, partiendo de esto se ubica en la diversidad de estrategias adaptadas a cada aspecto”. |
|
2 |
… “En todo momento de la ruina diaria, aplico una estrategia que ayude al desarrollo del pensamiento lógico matemático; ejemplo: al pedirle que realicen una formación se ubican detrás de o delante de, o cuando lo envían a la mesa manejamos cantidades y espacio”. |
|
3 |
… “partiendo de sus conocimientos, intereses y necesidades de los niños, se aplica la estrategia adecuada”. |
|
4 |
… “al momento de aplicar mis estrategias, en mi particular, las abordo donde los niños prefieran jugar, como lo es en el espacio de armar y construir y es allí donde desarrollamos el proceso lógico matemático”. |
|
5 |
… “Primero el nivel de aprendizaje de los estudiantes, ya que no puedo colocar actividades con alto nivel de complejidad que como docente sé que ellos no me puedan realizar; en segundo lugar, se debe tomar en consideración la aplicación de estrategias pedagógicas |
|
6 |
… “aplicar estrategias según la planificación a ejecutar visualizando los objetos, contar y escribir la cantidad, identificar número, sumas sencillas como tengo un caramelo y me regalan dos cuanto tengo en total eso me da a que el niño cuente y memorice, canción de números”. |
Fuente: información suministrada por los entrevistados.
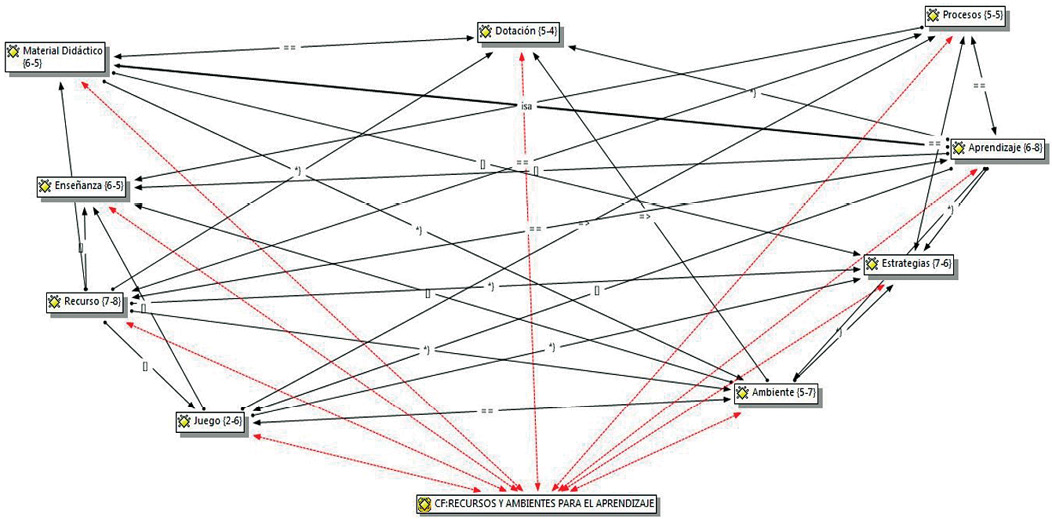
Figura 3. Red semántica: recursos y ambiente de aprendizaje
Tabla 5. Expresiones sobre los recursos y ambientes para el aprendizaje
|
Informante |
Unidad de análisis |
|
1 |
… “Una de las debilidades es la falta de material didáctico; sin embargo, con el poco recurso que se maneja se busca dar lo mejor para que el niño adquiera ese aprendizaje”. |
|
2 |
… “los recursos que poseo en mi ambiente de aprendizaje son los tacos, cuentos, figuras, entre otros”. |
|
3 |
… “Una de las debilidades es la falta de recurso didáctico”. |
|
4 |
… “al momento de aplicar mis estrategias, las debilidades es la falta de material didáctico...”. |
|
5 |
… “poseo poco conocimiento en cuanto a los niveles de aprendizaje pautados en la guía de indicadores”. |
|
6 |
… “Incumplimiento con la planificación del día pautado para aplicar las estrategias, también se podría decir la manera de manejar los recursos”. |
Fuente: información suministrada por los entrevistados.