Estrategia didáctica para fortalecer la competencia de comunicación matemática por medio de la fotografía
Didactic strategy to strengthen competence in mathematical communication through photography
Estratégia didática para fortalecer a competência de comunicação matemática através da fotografia
Beatriz Tirado Carvajala | Élgar Gualdrón Pintob,* | Adriana Ávila Záratec
a Institución Educativa Gonzalo Jiménez Navas, Floridablanca, Colombia
b Universidad de Pamplona, Pamplona, Colombia
c Universidad Autónoma de Bucaramanga, Bucaramanga, Colombia
Resumen
Presentamos los resultados de una investigación que estudió el fortalecimiento de la competencia de Comunicación Matemática, empleando la fotografía como mediador instrumental del aprendizaje, en estudiantes de noveno grado de una institución pública colombiana, mediante la implementación de una unidad didáctica relacionada con el pensamiento variacional, fundamentada en la teoría de las Situaciones Didácticas de Brousseau. Se trató de una investigación cualitativa con enfoque metodológico de investigación-acción, sustentada teóricamente bajo los planteamientos de Eisner. Se partió de un diagnóstico del nivel de Comunicación Matemática de los estudiantes por medio de una prueba tipo ICFES. Luego, se implementaron acciones encaminadas a mejorar dicha competencia mediante una unidad didáctica constituida por guías-taller. Los resultados sugieren que la fotografía es un medio didáctico que permite generar procesos de comunicación y de vinculación de la cotidianidad con las matemáticas, además de permitir al estudiante establecer regularidades y propiedades, reproducirlas mediante lenguaje matemático, usar nociones y procesos que lo llevan a construir representaciones, verificarlas y ponerlas a prueba. Dentro de las conclusiones, se pudo establecer que el uso de la fotografía en las clases de matemáticas favorece la motivación en los estudiantes, lo que sugiere una estrategia para hacer las clases más interesantes para ellos.
Palabras clave: competencia comunicativa, estrategia didáctica, fotografía, pensamiento variacional, visualización
Summary
We present the results of an investigation that studied the strengthening of mathematical communication skills, using photography as an instrumental mediator for learning. The study involved ninth grade students of a Colombian public institution, and it implemented a didactic unit related to variational thinking, based on the Brousseau theory of didactic situations. It was a qualitative investigation with an action-research methodological approach, theoretically supported by Eisner's approaches. The starting point was a diagnosis of the students' level of mathematical communication by means of an ICFES type test. Actions were then implemented to improve this competence by means of a didactic unit constituted by guides and workshops. The results suggest that photography is a didactic medium that allows the generation of communication processes and the linking of everyday life with mathematics, and allows students to establish regularities and properties, reproduce them through mathematical language, use notions and processes that lead them to construct representations, verify them and put them to the test. Among the conclusions, it could be established that the use of photography in mathematics classes favors students' motivation, making the classes more interesting for them.
Keywords: Communicative competence, didactic strategy, photography, variational thinking, visualization
Sumário
Apresentamos os resultados de uma pesquisa que estudou o fortalecimento da competência em Comunicação Matemática, utilizando a fotografia como mediador instrumental da aprendizagem,
em alunos da nona série de uma instituição pública colombiana, por meio da implementação de uma unidade didática relacionada ao pensamento variacional, baseado na teoria das situações drásticas de Brousseau. Foi uma pesquisa qualitativa, com uma abordagem metodológica de pesquisa-ação, apoiada teoricamente pelas abordagens de Eisner. A pesquisa partiu de um diagnóstico do nível de Comunicação Matemática dos alunos através de um teste tipo ICFES. Em seguida, ações destinadas a melhorar essa competência foram implementadas por meio de uma unidade didática composta por guias-oficinas. Os resultados sugerem que a fotografia é um meio didático que permite gerar processos de comunicação e vinculação do cotidiano com a matemática, além de permitir ao aluno estabelecer regularidades e propriedades, reproduzi-las através da linguagem matemática, utilizar noções e processos que o levam a construir representações, verificá-las e testá-las. Nas conclusões, foi possível estabelecer que o uso da fotografia nas aulas de matemática favorece a motivação dos alunos, o que sugere uma estratégia para tornar as aulas mais interessantes para eles.
Palavras-chave: Competência comunicativa, estratégia didática, fotografia, pensamento variacional, visualização
Entender la fotografía como un diálogo entre el creador y el observador que la lee resulta de gran importancia en el ámbito educativo. A pesar de que el significado de la imagen es personal, siguiendo a Vera, Allende y Villamizar (2018), brinda una gran posibilidad como medio en el desarrollo de diversas temáticas a nivel escolar. En la medida que el observador se entienda a sí mismo como recrea-dor, se enfrenta a un hecho de lectura que se abre a grandes posibilidades de desarrollo de conocimiento (Healey, 2016). No se trata solo de lo que el autor quería decir, sino de lo que recibió el lector y de lo que tiene que de-
cirle al fotógrafo (Colorado, 2014).
Por su parte, las matemáticas están constituidas por un conjunto de conocimientos mediante los cuales los seres humanos interpretan aspectos de la realidad y resuelven problemas de la vida cotidiana (Godino, Batanero & Font, 2004). Cada uno de sus conocimientos se expresan por medio de un conjunto de símbolos con los que se establecen relaciones y operaciones, que adquieren significado. De esta forma, aprender matemáticas significa aprender a pensar, hablar y escribir un lenguaje matemático. Es así como se establece una conexión entre la cotidianidad y la matemática (Monroy, 2017); dicha conexión permite sugerir a la fotografía como un mediador instrumental de aprendizaje. Este estudio contempla a la fotografía como eje central en el diseño de una estrategia didáctica basada en la teoría de las Situaciones Didácticas de Brousseau (2007), que aporte al aprendizaje significativo de los estudiantes de noveno grado de la institución educativa Gonzalo Jiménez Navas del municipio de Floridablanca, Santander, teniendo en cuenta los elementos de visualización propuestos por Gutiérrez (1991), para que hagan representaciones mentales que le ayuden a construir el conocimiento y, de esta forma, fortalecer su competencia comunicativa.
Marco teórico
Teoría de las Situaciones Didácticas
Con base en la teoría de Situaciones Didácticas de Brousseau (2007), una situación didáctica se concibe como un modelo de interacción entre el estudiante y el conocimiento a través de un medio o ambiente de aprendizaje, que es diseñado por el docente, en el que se tienen en cuenta los conocimientos previos y se promueve el aprendizaje autónomo, teniendo presente temas, reglas de interacción, materiales, un entorno, un medio y un procedimiento. De esta manera, se considera la fotografía como un mediador instrumental de aprendizaje con la que se diseñan situaciones de acción, de formulación y de validación:
• Situaciones de acción: en las que el estudiante entra en contacto con una actividad en donde la solución es básicamente el concepto que se quiere enseñar. Con este tipo de situaciones se pretende que el estudiante haga apreciaciones, proponga estrategias, tome decisiones, generalice, justifique, saque conclusiones y evalúe la eficacia de la experiencia para proponer nuevas estrategias que aborden la solución de un problema.
• Situaciones de formulación: en las que el estudiante propone modelos de solución de la situación teniendo en cuenta sus preconceptos, entra en comunicación con sus compañeros para elegir la mejor estrategia que permita la elaboración de conceptos o generalizaciones.
• Situaciones de validación: en las que el estudiante construye teorías, da argumentos para demostrar que sus razones son verdaderas, estas son puestas a prueba y son debatidas para llegar a un consenso.
Cabe preguntar ahora: ¿cuáles son las condiciones en las que se construye el conocimiento y los saberes? Según Brousseau (2007), los estudiantes se adaptan a las situaciones teniendo en cuenta la complejidad de las mismas, se debe crear la necesidad de “hacer descubrir” brindando diferentes tipos de información con el objetivo de producir nuevos conocimientos, que organizados y estructurados de manera lógica, los analicen, relacionen y generalicen para construir saberes y los pongan en práctica en la solución de situaciones contextualizadas (situaciones a-didácticas).
Visualización
Se parte de los planteamientos que hace De Guzmán (1996) al respecto, quien define la visualización de dos formas: por una parte, como un proceso mental para formar conocimiento y, por otra, como una competencia que se pone en práctica en la solución de problemas. Con la visualización es posible comprender diversos contenidos matemáticos utilizando la representación concreta; además, este proceso vincula la cotidianidad con las representaciones, permite abstraer propiedades y regularidades, hacer representaciones mentales, operaciones y generalizaciones para aplicarlas en la solución de problemas.
Otra definición en cuanto a este tema la hace Gutiérrez (1991), quien sugiere que la visualización está constituida por cuatro elementos: imágenes mentales, representaciones externas, procesos de visualización y habilidades de visualización (citado en Gualdrón, 2011).
Cabe preguntar ahora: ¿en qué consisten cada uno de estos cuatro elementos que constituyen la visualización?
[…] una imagen mental es cualquier clase de representación cognitiva de un concepto matemático o propiedad por medio de elementos visuales o espaciales; una representación externa es cualquier clase de representación gráfica de conceptos o propiedades incluyendo dibujos, bosquejos, diagramas, etc., que ayuda a crear o transformar imágenes mentales y a hacer razonamiento visual; un proceso de visualización es una acción mental o física en donde las imágenes mentales están involucradas. Las habilidades de visualización son aquellas que los individuos deben adquirir y perfeccionar para interpretar los procesos necesarios con imágenes mentales en la resolución de un problema (Gutiérrez, 1991, citado en Gualdrón, 2011, p. 49).
Este autor considera el proceso de visualización como una acción mental en donde entran en juego las acciones que se van a desarrollar y determina la interpretación de información figurativa (IFI, por sus siglas en inglés) que permite establecer convenciones, manejar vocabulario, hacer uso de diagramas, tablas y gráficas para hacer lecturas e interpretación de las mismas, y determina también el procesamiento visual (VP, por sus siglas en inglés) que permite reconocer patrones, establecer regularidades, analizar y sintetizar para resolver problemas.
En este orden de ideas, en el diseño de la unidad didáctica que se propuso en el estudio, se tuvo en cuenta que los procesos IFI y VP pudieran emerger con objeto de consolidar los aprendizajes deseables.
Teniendo en cuenta lo planteado con relación a la visualización, en esta investigación se consideran los mapas conceptuales como una forma de representación externa que permite a los estudiantes la construcción de su conocimiento. Esta herramienta les permite ser más autónomos, ya que participan de manera activa en la construcción del conocimiento (Novak & Musonda, 1991). Con los mapas conceptuales, los estudiantes pueden relacionar los conocimientos teniendo en cuenta sus pre-saberes, organizan los conocimientos de manera jerárquica y permiten ver el tema de manera integrada. Las representaciones mentales, por consiguiente, fortalecen el proceso de aprendizaje de los estudiantes, ya que promueve el desarrollo de procesos cognitivos, constructivos, metacognitivos y comunicativos.
Pensamiento variacional
y modelación matemática
En la investigación se abordaron la visualización y la representación gráfica con relación al concepto de función, que es un tema fundamental del currículo de matemáticas de noveno grado (MEN, 1998).
De acuerdo con lo anterior, el pensamiento variacional está relacionado con lo que cambia y lo que permanece constante, teniendo en cuenta los patrones y regularidades con que se repiten en ciertos procesos (Ordóñez-Ortega, Gualdrón-Pinto & Amaya-Franky, 2019). Así, dicho pensamiento requiere el uso de procesos de modelación, brindando al estudiante la capacidad de reconocer propiedades y reproducirlas mediante lenguaje matemático, para aplicarlos en la solución de situaciones en contexto de la vida cotidiana (Martínez-López & Gualdrón-Pinto, 2018).
Por otra parte, el componente de variación admite el uso de las tecnologías; según Vasco (2003), se puede recurrir a las tecnologías de la información y la comunicación (TIC) para fortalecer el pensamiento variacional y ejercitar la modelación, utilizando la simbología y el lenguaje matemático para construir gráficas, tabular datos, asignarle valores a las variables, comparar resultados, describir cambios, elaborar conclusiones y generalizaciones, y, posteriormente, formular un modelo. En este sentido, se recurrió al uso de la página web www.desmos.com como elemento pertinente al momento de desarrollar guías-taller, con objeto de crear representaciones mentales y construir conocimiento.
Ahora bien, vincular la cotidianidad en la creación de conocimientos es viable mediante el uso de la modelación en donde los estudiantes entran en contacto con la realidad; en este caso, por medio de la fotografía, identifican relaciones entre elementos, reconocen patrones y establecen regularidades, los utilizan en la construcción de representaciones mentales, que luego plasman en un modelo, para su posterior uso en la solución de problemas. Esto los lleva a desarrollar habilidades para que argumenten, comprendan el lenguaje propio de las matemáticas, interpreten significados, construyan representaciones y modelos y los pongan a prueba.
La matemática por medio de la fotografía
Es una constante escuchar que la enseñanza de la matemática se hace basada en definiciones, fórmulas y algoritmos, lo que conduce a los estudiantes a “ver” la matemática como algo sin sentido, donde no se observan claramente aplicaciones en la vida cotidiana.
Con respecto a esta constante, Villa-Ochoa, Bustamante, Berrío, Osorio y Ocampo (2008) proponen dar a la educación matemática un nuevo enfoque, en el que se reduzca la brecha entre los conceptos y la cotidianidad. También, en este sentido, los lineamientos curriculares de
matemáticas (MEN, 1998) y los estandartes básicos
de competencias en matemáticas (MEN, 2006) orientan las prácticas pedagógicas en la utilización de la matemática de una forma práctica y dinámica para la solución de situaciones del contexto.
Se piensa en la fotografía como medio para acceder al saber matemático, ya que con esta se pretende que los estudiantes registren de su entorno situaciones que estén relacionadas con conceptos matemáticos, para que con base en sus pre-saberes interpreten, relacionen, establezcan propiedades y patrones, usen lenguaje formal, construyan representaciones y modelos, que luego pondrán a prueba en la solución de situaciones matemáticas aplicadas en otros contextos.
Metodología
Diseño
La investigación presentó un enfoque cualitativo, enmarcado en un proceso de investigación-acción, teniendo como referentes los planteamientos de Carr y Kemmis (1990) y Eisner (1992). Dicho enfoque implicó el uso del diario pedagógico para registrar situaciones que se presentan en el aula de clase a lo largo del proceso y los avances de los estudiantes en el fortalecimiento del pensamiento matemático.
El estudio se desarrolló en cuatro fases, atendiendo a un proceso cíclico, que permitió reflexionar sobre la práctica pedagógica. Las fases de la propuesta, las actividades programadas y los recursos se encuentran condensados en la tabla 1.
Población y muestra
La investigación se desarrolló en el Colegio Gonzalo Jiménez Navas, ubicado en el municipio de Floridablanca, Santander, institución educativa de carácter oficial. La población, objeto de estudio, estuvo constituida por 117 estudiantes de grado noveno. La muestra estuvo conformada por 36 estudiantes del grado 9-2 (14-17 años) matriculados para el año lectivo 2017.
Consideraciones éticas
La validación de la prueba diagnóstica y la prueba final se realizaron de manera interna, ya que se usó el material correspondiente a las pruebas Saber 9° del ICFES del 2014 y 2015, respectivamente, en el área de matemáticas, en particular lo relacionado con la competencia de comunicación en el componente variacional. La validación del contenido por un experto se hizo para determinar si los instrumentos elaborados: cuestionarios, guías-taller, modelo del diario pedagógico, autoevaluación y matriz de referencia, eran apropiados para lograr el objetivo propuesto en la investigación, teniendo en cuenta el contexto y las condiciones escolares.
Los miembros de la línea de investigación Educación Matemática, del Grupo de investigación Edumatest, perteneciente a la Universidad de Pamplona, validaron la totalidad de los instrumentos aplicados a los estudiantes.
La investigación se orientó bajo aspectos éticos que permitieron la puesta en marcha, ejecución, utilización de resultados y evaluación de la propuesta pedagógica dentro de la institución educativa; entre ellos, están la autorización del rector del Colegio Gonzalo Jiménez Navas y el consentimiento informado, firmado por los padres de familia, en donde de forma escrita se socializó la propuesta
y se solicitó su correspondiente autorización para la participación voluntaria de los estudiantes.
Análisis y discusión
A continuación, se presentan los análisis y resultados de la información recolectada, usando para tal fin las categorías y los protocolos establecidos, incluyendo la triangulación correspondiente entre el marco teórico, la reflexión pedagógica como resultado de la investigación-acción y registros consignados en el diario pedagógico.
En cuanto a la prueba diagnóstica, esta se diseñó con base en 10 preguntas estandarizadas incluidas en la prueba Saber del ICFES para el grado noveno, aplicadas en el 2014 y se encuentra liberada en Internet. Con base en los parámetros propuestos por el ICFES, se diseñó una matriz de referencia (véase tabla 2), con la que se determinó el nivel de
competencia de los estudiantes. El nivel de desempeño
de los estudiantes es mínimo en la competencia de Comunicación Matemática, ya que el 84,025% de los estudiantes responden de manera correcta únicamente a preguntas de nivel mínimo, el 39,81% responde de manera correcta a preguntas de nivel satisfactorio, y solo el 13,86% responde acertadamente a preguntas de nivel avanzado, confirmando así que se requiere una intervención para mejorar los resultados en cuanto a dicha competencia.
Ahora bien, teniendo en cuenta los registros en el diario pedagógico, se pueden reconocer algunos aspectos que inciden de manera significativa en estos resultados, pues a pesar de que los estudiantes asumieron una actitud positiva frente al desarrollo de la actividad, a varios se les dificulta leer, interpretar, relacionar, entender el lenguaje matemático y resolver situaciones problema.
En cuanto al diseño e implementación de la estrategia didáctica, las guías-taller tienen en cuenta la categoría: estrategia didáctica y sus correspondientes subcategorías e indicadores, así:
Habilidades para el procesamiento visual: en estos ejercicios se alude a ¿qué hace el estudiante? Se tienen en cuenta los indicadores de la subcategoría B, fotografía, como son: B1, interpreta y B2, relaciona. Los estudiantes resuelven ejercicios en los que vinculan la cotidianidad con la matemática mediante el uso de registros fotográficos y los describen de forma literal, reconocen patrones y establecen regularidades entre distintas magnitudes que se les presentan.
Tabla 2. Matriz de referencia
|
Nivel |
Competencia de comunicación Componente variación |
|
Mínimo
|
|
|
Satisfactorio
|
|
|
Avanzado
|
|
Habilidades para interpretar información: en estos ejercicios se alude a ¿cómo lo hace? Se tienen en cuenta los indicadores de la subcategoría C, comunicación, como son: C1, usa lenguaje matemático y B2, construye representaciones. Los estudiantes resuelven ejercicios en los que expresen relaciones encontradas, en lenguaje algebraico para modelar situaciones y, además, elaboran diagramas, tablas y gráficas utilizando expresiones numéricas y algebraicas.
Habilidades para sistematizar, predecir y resolver: alude a ¿qué pasaría si…? Se tienen en cuenta los indicadores de la subcategoría D, pensamiento variacional, como son: D1, construye mapas conceptuales y D2, verifica y pone a prueba. Los estudiantes resuelven ejercicios en donde harán representaciones mentales, construyen modelos usando nociones y procesos, recurriendo a la página web www.desmos.com; además, solucionan situaciones matemáticas relacionadas con variación, no rutinarias y de mayor dificultad, argumentando procesos.
En el proceso de diseño se tuvo en cuenta la teoría de las Situaciones Didácticas de Brousseau (1986), en donde inicialmente el estudiante actúa enfrentándose a la solución de ejercicios de manera individual, buscando fortalecer su autonomía y los procesos de visualización IFI y VP.
Las situaciones propuestas a los estudiantes parten de los registros fotográficos con los que interactúan con el entorno, de los que se seleccionan y que de manera intencionada sirvan para abordar los temas y diseñar las preguntas, en donde se requiere que los estudiantes realicen procesos visuales, como descripciones literales de imágenes fotográficas, luego pasen a identificar en ellas los elementos que la componen y expresen cómo están relacionados dichos elementos. En este proceso inicial se tienen en cuenta los aspectos de la subcategoría B.
Inicialmente, en este tipo de ejercicios, a los estudiantes, aunque reconocen los elementos en cada fotografía, se les dificulta expresar con sus palabras lo que ven en las imágenes, les falta fluidez verbal, muestran timidez y falta de confianza para dar a conocer sus apreciaciones. A medida que se implementaban las guías-taller, el proceso de descripción literal mejoró: los estudiantes mostraron más organización en sus producciones y describieron más detalles de las imágenes presentadas. En cuanto al proceso de reconocimiento de patrones, establecieron regularidades y dieron argumentos con mayor fluidez. A partir de las fotografías, se propusieron ejercicios para elaborar diferentes conceptos relacionados con la variación. En esta parte del proceso, los estudiantes respondieron a preguntas planteadas con respecto a los procesos IFI y VP. Las situaciones matemáticas que componen las guías-taller se diseñaron para que los estudiantes observen la imagen y con el razonamiento visual, determinen los elementos que se encuentran en ella y establezcan regularidades.
En las figuras 1 y 2 se presentan algunas imágenes que ejemplifican los análisis anteriores.
Luego, se proponen ejercicios en donde los estudiantes pasan a trabajar en grupo, que atendiendo a Brousseau (1986), es en este momento donde hacen formulaciones, discuten, argumentan y eligen un representante para hacer luego una puesta en común. Las situaciones propuestas responden al proceso de visualización representación externa, es el momento donde se requiere que los estudiantes expresen en símbolos matemáticos las relaciones, que de manera reiterada, encontraron en las imágenes; elaboren gráficas, diagramas y tablas. En esta parte del proceso se tienen en cuenta los indicadores de la subcategoría C.
En este tipo de ejercicios cabe destacar que, inicialmente, a los estudiantes se les dificulta expresar las relaciones que encuentran en una imagen de manera reiterada en símbolos; no tienen dominio de las expresiones algebraicas; presentan dudas para construir tablas de valores, pues se les dificulta calcular el valor numérico. En cuanto a la elaboración de gráficas, no recuerdan cómo ubicar puntos en el plano cartesiano; se les dificulta sacar conclusiones, les falta dominio en las argumentaciones, pues carecen del vocabulario matemático necesario para expresarlo de manera clara y fluida.
A medida que se implementan las guías-taller, los estudiantes van avanzando en su proceso, de tal forma que plasman por medio de representaciones externas las propiedades encontradas, recurriendo a la elaboración de tabla de valores y mediante símbolos matemáticos representen la variación de las magnitudes involucradas y, posteriormente, elaboran la gráfica correspondiente, analizando y argumentando algunas características de la gráfica dibujada. Al revisar las producciones elaboradas por los estudiantes, se puede apreciar que han consolidado el proceso de visualización, puesto que han extractado información de las fotografías para resolver los ejercicios propuestos, dando argumentos “informales” para justificar: ¿qué hace? y ¿cómo lo hace?
En este momento del estudio, los estudiantes establecen relaciones entre las diferentes formas de expresar una función; se muestran más seguros del proceso; demuestran que conocen y manejan los conceptos; su capacidad de argumentar la ponen en juego en la solución de los ejercicios. En el desarrollo de las actividades se nota el progreso en cuanto al desempeño en la solución de situaciones matemáticas y la aplicación de los procesos de visualización IFI, VP y representaciones externas. El uso
de la fotografía es favorable en la elaboración de representaciones mentales, pues recuerdan y asocian los conceptos con la solución de situaciones y demuestran que han afianzado el proceso de visualización; utilizan el lenguaje matemático a la hora de describir relaciones y han entrado en el proceso formal de modelación. En las figuras 3, 4, 5, 6 y 7 se muestran evidencias de los avances presentados por algunos estudiantes en el proceso de representación externa.

Figura 3. Ejercicio categoría C1

Figura 4. Ejercicio categoría C1

Figura 5. Ejercicio categoría C2
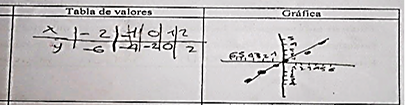
Figura 6. Ejercicios categoría C2
Figura 7. Ejercicios categorías C1 y C2
Para continuar con el proceso, se pasó después a las situaciones de validación, en donde, según Brousseau (1986), el estudiante construye el conocimiento a través de modificaciones o adaptaciones de sus pre-saberes. De esta forma, se proponen situaciones en donde el estudiante fortalece sus procesos de visualización en cuanto a imágenes mentales y sus habilidades de visualización. Es en este momento donde los estudiantes hacen representaciones mentales y construyen modelos, que luego los verifican y ponen a prueba en la solución de situaciones matemáticas en otros contextos; son las llamadas situaciones a-didácticas propuestas por Brousseau (2007).
Para reforzar estos procesos, se acude a la modelación por medio de mapas conceptuales, utilizando los aspectos contemplados por Novak y Musonda (1991), con los que los estudiantes hacen representaciones mentales y construyen modelos de funciones, pendiente de una recta, función lineal, cuadrática, exponencial y logarítmica. También se utiliza la herramienta desmos, que le permite
a los estudiantes realizar procesos de análisis alrededor de
los cambios que ocurren a una gráfica si se varían algunos elementos de una función; facilitando de esta manera la transformación de las imágenes mentales y mejorar sus procesos de modelación. En esta parte del proceso se tienen en cuenta los indicadores de la subcategoría D.
Inicialmente, ante este tipo de situaciones, los estudiantes se apoyan en el trabajo colaborativo, dan opiniones, sacan conclusiones, eligen un representante y socializan lo trabajado, exponen sus ideas mediante mapas conceptuales. Las representaciones externas se aproximan regularmente a los parámetros establecidos.
A medida que se implementan las guías-taller, el proceso de representación mental va mejorando, aunque aún no se animan a trabajar de manera individual, pues manifiestan que tienen dudas en cómo organizar sus ideas. En cuanto a la competencia de comunicación, cabe anotar que el manejo de procesos de visualización avanza un poco más, ya que los estudiantes demuestran en sus acciones y en las respuestas, haber adquirido habilidades para elaborar conclusiones, hacer representaciones mentales de conceptos mediante la construcción de modelos.
El uso de la herramienta desmos permite afianzar los procesos de modelación, pues permite realizar gráficas de funciones de una manera sencilla y rápida. Este proceso les brindó bases con las que posteriormente construyeron mapas conceptuales y les permitió afianzar el proceso de visualización, ya que al hacer razonamiento visual, elaboran representaciones externas y, de esta manera, van creando imágenes mentales y adquieren habilidades para sistematizar, predecir y resolver situaciones justificando lo relacionado a ¿qué pasaría si…?
Posteriormente, se proponen situaciones en donde deben establecer relaciones de comparación entre diferentes gráficas. En cuanto a la solución de situaciones problema, los estudiantes han mejorado sus habilidades para leer, interpretar, reconocer aspectos relevantes y proponer alternativas de solución, en donde tienen que verificar y poner a prueba sus conceptos. Las situaciones presentadas son de la vida cotidiana, situaciones matemáticas no rutinarias y de mayor dificultad, relacionadas con matemática financiera o con la asignatura de física. El proceso avanza al nivel en que los estudiantes establecen relaciones de comparación entre diferentes imágenes y utilizan representaciones algebraicas para modelar situaciones problema. En este momento del desarrollo, se observa que los estudiantes han adquirido un nivel de desempeño avanzado. En las figuras 8, 9 y 10 se muestra el avance de los estudiantes en la elaboración de mapas conceptuales.
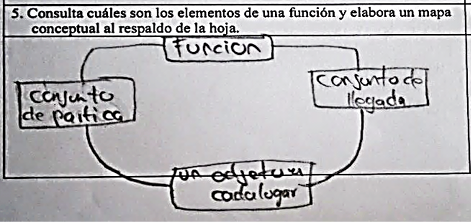
Figura 8. Ejercicio categoría D1
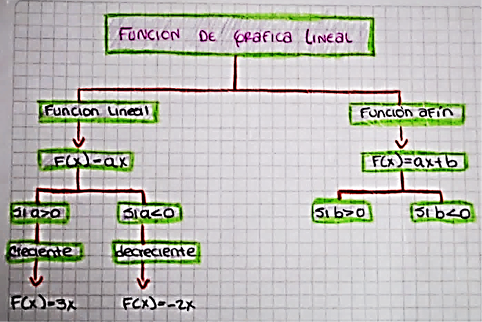
Figura 9. Ejercicio categoría D1

Figura 10. Ejercicios categoría D2
Con la implementación de las guías-taller, los estudiantes muestran que han afianzado el proceso de visualización, que les permite formar conocimiento y desarrollar habilidades y competencias para resolver situaciones cotidianas y, de esta forma, mejorar su competencia de Comunicación Matemática.
En cuanto a la efectividad de la estrategia didáctica implementada, se aplicó una prueba final de 10 preguntas, diseñada teniendo en cuenta la prueba Saber de noveno grado correspondiente al 2015 del ICFES, cuyos términos y condiciones de uso permiten su aplicación con fines investigativos. Para su análisis, se utilizó la matriz de referencia (véase tabla 2) y arrojó los siguientes resultados: el 81,24% de los estudiantes responden de manera correcta a preguntas de nivel mínimo, el 61,09% responden de manera correcta a preguntas de nivel satisfactorio y el 34,17% de los estudiantes responden de manera correcta a preguntas formuladas de nivel avanzado. Comparado con los resultados que arrojó la prueba diagnóstica con la prueba final, se puede concluir que la implementación de la estrategia didáctica a partir de la fotografía, como mediador instrumental del aprendizaje, es pertinente para fortalecer la competencia de Comunicación Matemática.
Conclusiones
Por medio de la fotografía se puede lograr un aprendizaje significativo que le permite al estudiante asociar los conceptos con su correspondiente aplicación y, de esta manera, construir conocimiento. Sin embargo, la fotografía por sí misma no genera conocimiento, es necesario enmarcarla dentro de una didáctica que promueva una genuina comprensión y construcción de los conceptos matemáticos.
El introducir el uso de la fotografía en el currículo de matemáticas exige al profesor gestionar de manera diferente sus clases, así como la planificación del curso. En este sentido, a la fotografía se la puede considerar un mediador instrumental de aprendizaje útil para implementar estrategias didácticas que permiten desarrollar procesos de visualización y fortalecer la competencia de Comunicación Matemática.
Los mapas conceptuales, como representación externa, son útiles para fortalecer el desarrollo de procesos de pensamiento, pues le permiten al estudiante establecer relaciones significativas entre conceptos; además, el profesor puede determinar el grado de comprensión que los estudiantes han adquirido en el proceso de aprendizaje.
La estrategia didáctica centrada en la fotografía le permitió a los estudiantes mejorar sus habilidades de Comunicación Matemática como son: describir en forma literal lo visualizado en las imágenes, reconocer patrones, establecer regularidades entre magnitudes, usar lenguaje matemático para modelar situaciones, elaborar tablas, diagramas y gráficas utilizando expresiones numéricas y algebraicas, hacer representaciones mentales y construir modelos por medio de mapas conceptuales y resolver situaciones de aplicación en otros conceptos.
El uso de la página www.desmos.com fue acertado, pues generó motivación e interés, además posibilitó que los estudiantes establecieran comparaciones entre magnitudes, permitió establecer diferencias y regularidades a partir de la variación de algunos elementos en las funciones, fue un medio con el que el estudiante pudo desarrollar habilidades para sistematizar, predecir y determinar ¿qué pasaría si…?, facilitándole la elaboración de modelos y creación de conceptos.
Por último, los resultados sugieren que la fotografía es un medio que permite diseñar actividades en las que el estudiante contextualiza las matemáticas con la vida cotidiana, construye conocimiento alrededor de diferentes objetos matemáticos, y fortalece habilidades y competencias para resolver situaciones prácticas y reales.
Reconocimientos
Este artículo se derivó del trabajo de investigación de maestría Estrategia didáctica para fortalecer la competencia comunicación matemática a través de la fotografía, en estudiantes de noveno grado de la Institución Educativa Gonzalo Jiménez Navas de Floridablanca, desarrollada en la Universidad Autónoma de Bucaramanga (UNAB).
Referencias
Brousseau, G. (1986). Fondements et méthodes de la didactiques des mathématiques. Recherches en Didactique des Mathematiques, 7(2), 33-115.
Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Buenos Aires: Libros del Zorzal.
Carr, W., & Kemmis, S. (1990). Teoría crítica de la enseñanza: la investigación-acción en la formación del profesorado. Barcelona: Martínez Roca.
Colorado, O. (2014). How to read a photograph without dying in the attempt [blog post]. Recuperado de https://oscarenfotos.com/2013/10/07/lectura-fotografica/.
De Guzmán, M. (1996). El papel de la visualización. Ensayos de visualización en análisis matemático. Madrid: Pirámide.
Eisner, E. (1992). La investigación-acción en educación. Madrid: Morata.
Godino, J., Batanero, C., & Font, V. (2004). Didáctica de las matemáticas para maestros. Granada: Departamento de Didáctica de la Matemática. Facultad de Ciencias de la Educación. Universidad de Granada.
Gualdrón, E. (2011). Análisis y caracterización de la enseñanza y aprendizaje de la semejanza de figuras planas (tesis Doctorado). España: Universidad de Valencia.
Gutiérrez, A. (1991). Procesos y habilidades en visualización espacial. Memorias del Tercer Congreso Internacional sobre Investigación en Educación Matemática. España: Universidad de Valencia.
Healey, D. (2016). Why your school be teaching photography. Recuperado de https://www.tes.com/news/why-your-school-should-be-teaching-photography
Martínez-López, L. G., & Gualdrón-Pinto, E. (2018). Fortalecimiento del pensamiento variacional a través de una intervención mediada con TIC en estudiantes de grado noveno. Revista de Investigación, Desarrollo e Innovación, 9(1), 91-102.
MEN. (1998). Lineamientos curriculares de matemáticas. Bogotá. Recuperado de http://www.mineducacion.gov.co/1621/articles-339975_matematicas.pdf.
MEN. (2006). Estándares básicos de competencias en matemáticas. Bogotá. Recuperado de https://www.mineducacion.gov.co/cvn/1665/articles-116042_archivo_pdf2.pdf.
Monroy, O. (2017). Las matemáticas en la vida diaria y la ciencia. Iberoamérica divulga. Recuperado de https://www.oei.es/historico/divulgacioncientifica/?Las-Matematicas-en-la-vida-diaria-y-la-Ciencia.
Novak, J. D., & Musonda, D. (1991). A twelve-year longitudinal study of science concept learning. American Educational Research Journal, 28, 117-153. https://doi.org/10.3102/00028312028001117.
Ordóñez-Ortega, O., Gualdrón-Pinto, E., & Amaya-Franky, G. (2019). Pensamiento variacional mediado con baldosas algebraicas y manipuladores virtuales. Revista de Investigación, Desarrollo e Innovación, 9(2), 345-360.
Vasco, C. (2003). El pensamiento variacional y la modelación matemática. XI CIAEM, Brasil: Universidad Regional de Blumenau.
Vera, L. A., Allende, J. J., & Villamizar, Y. (2018). Photographs as a pedagogical tool to strengthen the reading and writing competences. Revista Logos Ciencia & Tecnología, 10(4), 20-33. http://dx.doi.org/10.22335/rlct.v10i4.609.
Villa-Ochoa, J. A., Bustamante, C., Berrío, M., Osorio, A., & Ocampo, A. (2008). El proceso de modelación matemática en las aulas escolares. A propósito de los 10 años de su inclusión en los lineamientos curriculares colombianos. 9º Encuentro Colombiano de Matemática Educativa, Valledupar, Colombia. Recuperado de http://funes.uniandes.edu.co/936/1/4Cursos.pdf.


