Análisis del comportamiento dinámico de una suspensión
de vehículo independiente de doble horquilla
Analysis of the dynamic behavior of an independent double wishbone vehicle suspension
Análise do comportamento dinâmico de uma suspensão duplo A de veículo independente
Nelson Arzola de la Peña* | César Andrés Castro Torres
a Facultad de Ingeniería, Departamento de Ingeniería Mecánica y Mecatrónica, Grupo de Investigación en Diseño Óptimo Multidisciplinario, Universidad Nacional de Colombia, Bogotá, Colombia
Resumen
El artículo muestra un modelo teórico, programado con el software Matlab, que permite el análisis dinámico de una suspensión independiente de doble horquilla. La validación se realiza mediante un banco de pruebas y un modelo experimental, el cual permite adquirir datos sobre el comportamiento dinámico en función de dos parámetros fundamentales: amplitud y frecuencia de oscilación, los cuales representan el perfil del terreno y la velocidad lineal del vehículo, respectivamente. Se obtienen gráficas de posición, velocidad, aceleración y fuerzas sobre cada par cinemático y los centros de gravedad de cada componente, además de las fuerzas ejercidas por cada uno de los elementos que conforma el conjunto resorte-amortiguador, todos estos resultados en función de los dos parámetros fundamentales mencionados.
Palabras clave: Dinámica vehicular, suspensión de doble horquilla, diseño factorial, amplitud de oscilación, frecuencia de oscilación
Summary
The article presents a theoretical model, programmed with Matlab software, which allows the dynamic analysis of an independent double wishbone suspension. The validation is performed by means of a test bench and an experimental model, which makes it possible to acquire data on the dynamic behavior according to two fundamental parameters: oscillation amplitude and oscillation frequency, which represent the terrain profile and the linear speed of the vehicle, respectively. Graphs are obtained of position, speed, acceleration and forces on each kinematic torque and the centers of gravity of each component, as well as the forces exerted by each of the elements that make up the spring-shock assembly. All of these results are based on the two fundamental parameters mentioned above.
Keywords: Vehicle dynamics, double wishbone suspension, factorial design, oscillation amplitude, oscillation frequency
Sumário
O artigo mostra um modelo teórico, programado com o software Matlab, que permite a análise dinâmica de uma suspensão duplo A independente. A validação é realizada por meio de uma bancada de testes e um modelo experimental, que permite adquirir dados sobre o comportamento dinâmico com base em dois parâmetros fundamentais: amplitude e frequência de oscilação, que representam o perfil do terreno e a velocidade linear do veículo, respetivamente. São obtidos gráficos de posição, velocidade, aceleração e forças sobre cada par cinemático e os centros de gravidade de cada componente, além das forças exercidas por cada um dos elementos que compõem o conjunto de mola-amortecedor, em que todos esses resultados dependem dos dois parâmetros fundamentais mencionados.
Palavras-chave: Dinâmica veicular, suspensão dulo A, desenho fatorial, amplitude de oscilação, frequência de oscilação
La suspensión es uno de los siete sistemas fundamentales del vehículo automotor, y tiene como cometido “absorber” las irregularidades del terreno sobre el que se desplaza, a la vez que mantiene las ruedas en contacto con el terreno, proporcionando a los pasajeros un adecuado nivel de confort y seguridad de marcha, protegiendo la carga y las piezas del automóvil (Morello, Genta, Cavallino & Filtri, 2014).
El vehículo automotor se ve sometido a factores que afectan su comportamiento, como son los cambios de velocidad del vehículo durante el proceso de frenado, la maniobrabilidad del piloto sobre la conducción, las condiciones topográficas, orográficas y climáticas de la región donde este trabaje. Las exigencias a las que se encuentre sometida la suspensión del automotor deben estudiarse a fondo, ya que de ella se desprende fundamentalmente todas las situaciones de comportamiento dinámico del vehículo.
El sistema de suspensión de un vehículo materializa la unión entre los conceptos de masa suspendida y masa no suspendida (Mantilla, 2014). La masa suspendida es aquella que integra todos los elementos cuyo peso es soportado por el bastidor del vehículo (grupo motriz, carrocería, pasajeros, etc.). Mientras que la masa no suspendida comprende los demás componentes no soportados por el bastidor (ruedas, elementos estructurales de la suspensión, amortiguadores, frenos, etc.).
En la actualidad, el sistema de suspensión de los vehículos debe cumplir con una serie de requerimientos en relación con las diferentes condiciones de funcionamiento, ya sea acelerar, frenar, girar o la combinación de estas condiciones respecto a las irregularidades del terreno; además, existen diferencias entre una suspensión para eje delantero y para eje trasero, variando los requerimientos de diseño (Morello et al., 2014). Por ello, existe una gran variedad de configuraciones en un sistema de suspensión. Los distintos tipos de suspensión pueden clasificarse en tres grandes categorías: independiente, semiindependiente y dependiente.
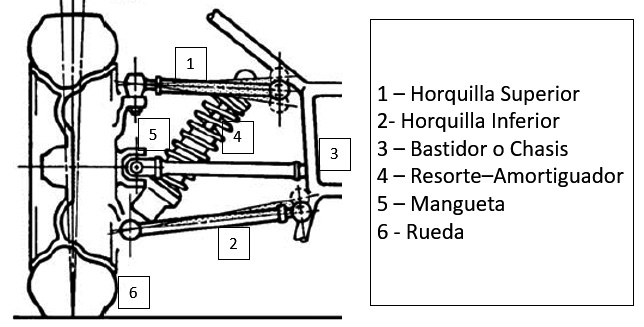
En esta investigación se trabajará una suspensión independiente de doble horquilla, la cual ofrece una mejor calidad de conducción y características de manejo, gracias al menor peso no suspendido y la capacidad de cada rueda para abordar la carretera sin estar sometida al comportamiento
dinámico de la otra rueda existente sobre un mismo eje, como sucede con la suspensión dependiente (Tanik & Parlaktaş, 2015). En la figura 1 se muestra de forma esquemática las partes de una suspensión de doble horquilla.
La función principal de los componentes flexibles en una suspensión es garantizar la adaptación a las irregularidades del terreno (Buitrago, 2011). Estos elementos garantizan el confort de la conducción almacenando la energía cinética
generada por la carrera de la suspensión como energía
elástica (Morello et al., 2014). Además, la posición de este elemento se diseña con el objetivo de que la fuerza máxima proveniente de un impacto se transfiera al resorte logrando proteger el bastidor (Thakare, Antapurkar,
Shah, Dhamangaonkar & Sapali, 2015). El parámetro fundamental es el coeficiente de rigidez elástico, que se define como la relación entre la fuerza (o torque) que ejerce el componente elástico y su deformación lineal (o angular). Existen distintos tipos de soluciones aplicables al sistema de suspensión de un vehículo, entre ellos se encuentran los muelles de ballesta, helicoidal, de torsión, de goma y de gas, entre otros (Morello et al., 2014).
Por otro lado, los componentes de amortiguación tienen como función principal disipar las oscilaciones de la masa suspendida originadas por el elemento flexible al adaptarse a las irregularidades del terreno. Quien materializa esta función, es el amortiguador, existen dos diferentes tipos de amortiguadores: por fricción sólida y los hidráulicos (fricción viscosa). Los amortiguadores por fricción sólida son muy poco usados en la actualidad gracias a la aparición de los amortiguadores hidráulicos, ya que estos ofrecen un mejor desempeño (Datte & Ross, 2016). El amortiguador más usado en la actualidad en los vehículos es el hidráulico con configuración telescópica. El parámetro
fundamental que define a un amortiguador es el coeficiente de amortiguación. Este último varía de acuerdo con el tipo de vehículo debido a las condiciones de trabajo, se define como la relación entre la fuerza ejercida y la velocidad a la que se mueve el pistón del amortiguador.
Como componentes fundamentales se muestran los trapecios de suspensión, son los elementos que se encuentran anclados al bastidor o chasis del vehículo en la parte superior e inferior del sistema de suspensión por medio de cojinetes, lo que permite el movimiento de estos alrededor de un eje. En el otro extremo se ensambla la mangueta mediante rótulas que permiten el movimiento en tres direcciones (Sanz, 2015).
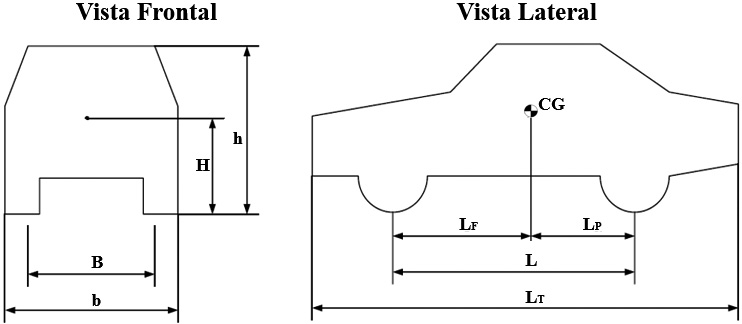
Todo vehículo tiene definidas unas dimensiones generales que establecen su configuración básica. En la figura 2 y con la ayuda de la tabla 1 se representan las dimensiones generales importantes para analizar un vehículo de dos ejes (Güler, 2006).
Tabla 1. Descripción de parámetros para la configuración básica del vehículo (Güler, 2006)
|
Parámetro |
Descripción |
|
b |
Ancho del vehículo |
|
B |
Ancho de vía del eje delantero |
|
h |
Altura del vehículo |
|
H |
Altura del centro de gravedad del vehículo |
|
LT |
Largo del vehículo |
|
L |
Distancia entre ejes |
|
LF |
Distancia del eje frontal al centro de gravedad |
|
LP |
Distancia del eje posterior al centro de gravedad |
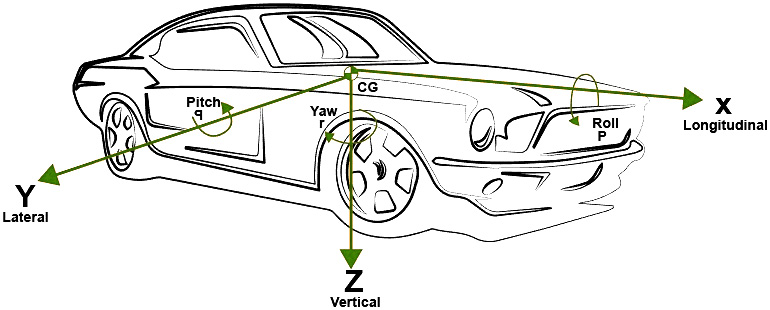
Existen dos tipos de sistemas de coordenadas, como lo establece la ISO 8855 o la SAE (ISO 8855, 2011; Vega, Llanes-Cedeño & Molina, 2018). El común de las dos normas reside en que su origen se centra en el centro de gravedad del vehículo y se emplea un sistema de coordenadas cartesianas. En la figura 3 se representa el sistema coordenado y los giros asociados a cada eje para el análisis del comportamiento dinámico de un vehículo (Dixon, 2009).
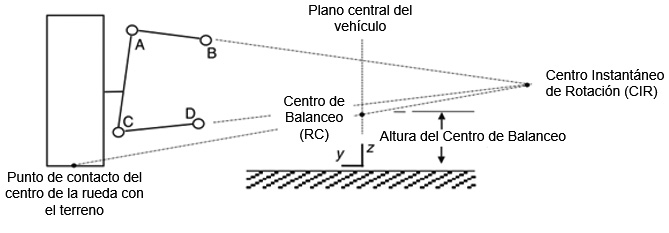
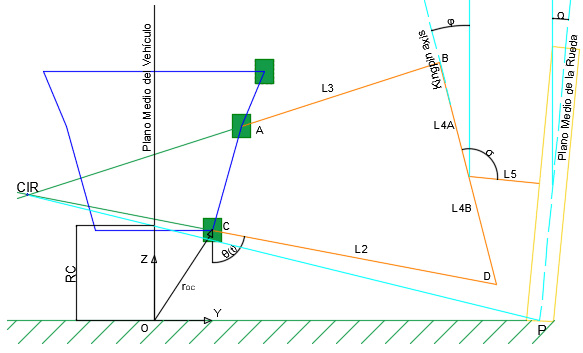
Observando la suspensión desde la vista frontal del vehículo, y al prolongar las rectas que corresponden a los brazos de suspensión superior e inferior, existe un punto en el cual se intersecan, a este punto se le denomina el “centro instantáneo de rotación” (Dixon, 2009; Giovanny, 2012). El centro instantáneo de rotación de la suspensión es el punto sobre el cual girará la rueda y, por tanto, respecto a la posición espacial de este punto se realizará un cambio en el ángulo de caída (Camber) al desplazarse la rueda verticalmente. La representación geométrica de este punto se muestra en la figura 4. Además, es importante definir la ubicación del centro de balanceo (véase figura 4), el cual se encuentra realizando la unión desde el centro instantáneo de rotación al punto medio de contacto del neumático con el suelo; en el punto en el que se intersecan esta recta creada anteriormente con
el eje vertical del vehículo se localiza el centro de balanceo (Blundell & Harty, 2014; Giovanny, 2012).
Una medida de importancia es la distancia de este centro de balanceo al centro de gravedad del vehículo, el cual se denomina brazo de momento; esta distancia define el
balanceo (roll) del vehículo. A mayor distancia, mayor
balanceo, mientras que a menor distancia ocurre lo contrario (Giovanny, 2012).
El presente trabajo tiene como propósito realizar un estudio detallado sobre el comportamiento dinámico de un vehículo, mediante el desarrollo de modelos teóricos y de simulación, los cuales son contrastados con resultados experimentales obtenidos con la ayuda de un banco de pruebas especialmente desarrollado para la presente investigación. La obtención de modelos matemáticos validados para una suspensión de doble horquilla es de gran importancia para una mejor comprensión del comportamiento en operación de una suspensión y el diseño de nuevas configuraciones o modificaciones sobre geometrías ya existentes en los sistemas de suspensión de los automóviles. Además, pueden realizarse predicciones y comprobaciones a un costo razonable sobre el comportamiento del vehículo respecto a ciertas condiciones dadas.
Materiales y métodos
Planteamiento del modelo dinámico para la suspensión
El modelo teórico del fenómeno se plantea con ¼ de vehículo, para ello se han considerado modelos previos desarrollados por Rojas y Arzola (2013), Thacker (2015) y por Yu, Evangelou y Dini (2017); ya que cada configuración de suspensión tiene sus propios pros y contras cuando se trata de ganancias de inclinación respecto al centro de
balanceo e inclinación debido al movimiento vertical
de la rueda (bump y rebound) (Schommer, Soliman, Farias & Martins, 2015). Este modelo teórico puede desarrollarse para cualquier tipo de configuración geométrica de una suspensión de doble horquilla; esto contempla, por ejemplo, suspensiones con brazos paralelos e iguales,
paralelos y con la misma inclinación, paralelos no iguales, y
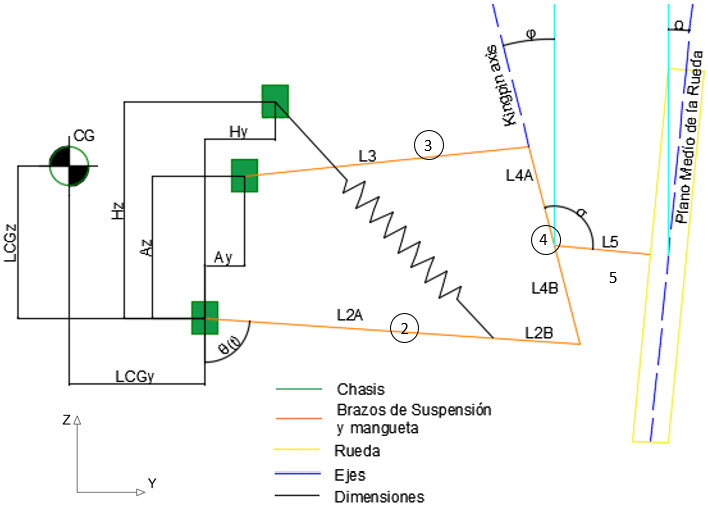
brazos convergentes o divergentes con longitudes de brazos diferentes. En la figura 5 se muestran los parámetros geométricos de la configuración de la suspensión de
doble horquilla, mientras que las variables asociadas a los esquemas mostrados anteriormente se encuentran
descritas en la tabla 2.
Para describir la cinemática y la cinética del comportamiento de la suspensión es necesario encontrar las funciones que describen el movimiento de las juntas
del mecanismo, así como las posiciones de los centros de
masa de cada uno de los eslabones que componen
el mecanismo. Para ello, se modela el comportamiento del mecanismo de cuatro barras usando mecánica vectorial para un movimiento plano. Esto debido a que los fenómenos más importantes ocurridos sobre una suspensión de doble horquilla se dan sobre el plano, además de que este estudio permite observar el comportamiento de parámetros como centro de balanceo, centros instantáneos de rotación, ángulo de caída, entre otros.
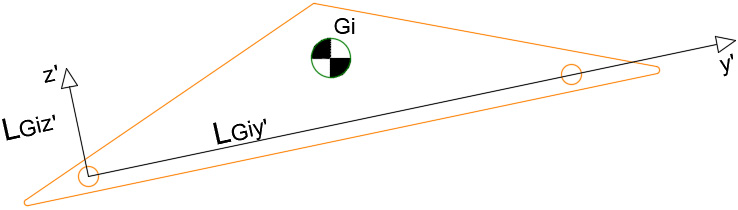
Como parte del análisis dinámico es importante definir la posición, velocidad y aceleración de los centros de masa de cada uno de los eslabones. En la figura 6 se muestra el
esquema general de cualquier eslabón del mecanismo.
El centro de masa se ubica respecto a un sistema de referencia prima anclado al eslabón bajo estudio, luego se realiza la transformación de coordenadas para hallar la posición del centro de masa respecto al sistema de referencia global de la suspensión. El procedimiento se repite para cada uno de los eslabones de la suspensión mediante un análisis trigonométrico. Luego, con la primera y segunda
derivada de las funciones obtenidas se hallan las funciones de velocidad y aceleración, respectivamente.
La matriz de análisis de las velocidades angulares para la suspensión queda expresada así:
 (1)
(1)
Luego, mediante el análisis de las aceleraciones se obtiene la matriz de solución para las aceleraciones angulares de los eslabones que conforman el mecanismo de la suspensión:
 (2)
(2)
El análisis de fuerzas en los pares cinemáticos se realiza basado en Norton (2013). El método de solución es el newtoniano y se aplican las leyes de movimiento para un mecanismo plano mediante las expresiones:
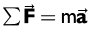 (3)
(3)
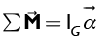 (4)
(4)
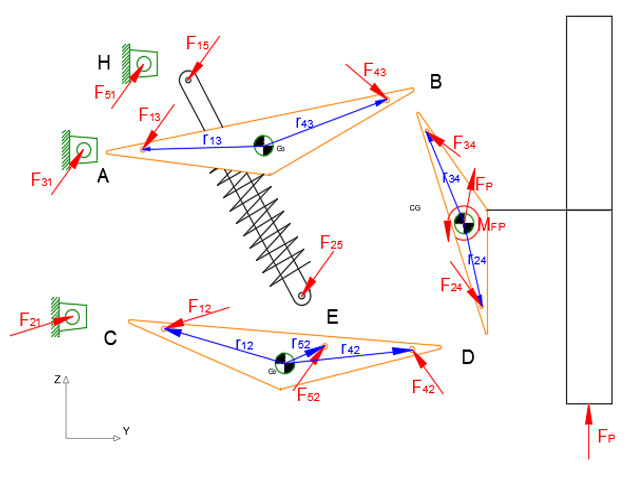
Es necesario hacer el diagrama de cuerpo libre para cada uno de los eslabones del mecanismo. Las masas y los momentos de inercia principales de cada componente son determinados mediante el software CAD, considerando la geometría detallada y la densidad del material del que están construidos. En la figura 7 se muestra el análisis, la notación Fij usada refiere a la fuerza ejercida del cuerpo i sobre el cuerpo j.
Desarrollando para cada componente (3) y (4) de acuerdo con el diagrama de cuerpo libre de la figura 7, se obtiene la matriz de solución de la cinética de la suspensión:
 (5)
(5)
Se encuentra a continuación la ubicación del centro instantáneo de rotación. La solución se obtiene aislando y analizando el triángulo CIR-B-D de acuerdo con la figura 8. Además, otro asunto de interés es la determinación del centro de balanceo, el cual se obtiene aislando y analizando el triángulo formado por los puntos CIRz-CIRy-P.
La posición del centro instantáneo de rotación (CIR) sobre el sistema coordenado Y-Z puede hallarse por medio de:
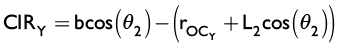 (6)
(6)
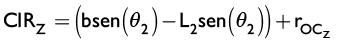 (7)
(7)
Donde b es la longitud de la línea que unen los puntos CIR y P; 2 es el ángulo formado entre la línea horizontal y b; 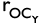 y
y 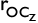 son las componentes del vector que define el punto material C dentro del sistema de coordenadas global; L2 es la longitud del brazo inferior de suspensión y CIRy y CIRz son las componentes del vector que define el centro instantáneo de rotación dentro del sistema
son las componentes del vector que define el punto material C dentro del sistema de coordenadas global; L2 es la longitud del brazo inferior de suspensión y CIRy y CIRz son las componentes del vector que define el centro instantáneo de rotación dentro del sistema
de coordenadas global.
Por otro lado, la ubicación del centro de balanceo (RC) respecto al sistema coordenado Y-Z se encuentra como:
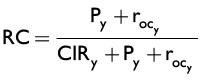 (8)
(8)
Donde Py es la posición horizontal (sobre el eje Y) desde el punto C (articulación del brazo inferior en el chasis) al punto P (punto medio de contacto de la rueda con el terreno).
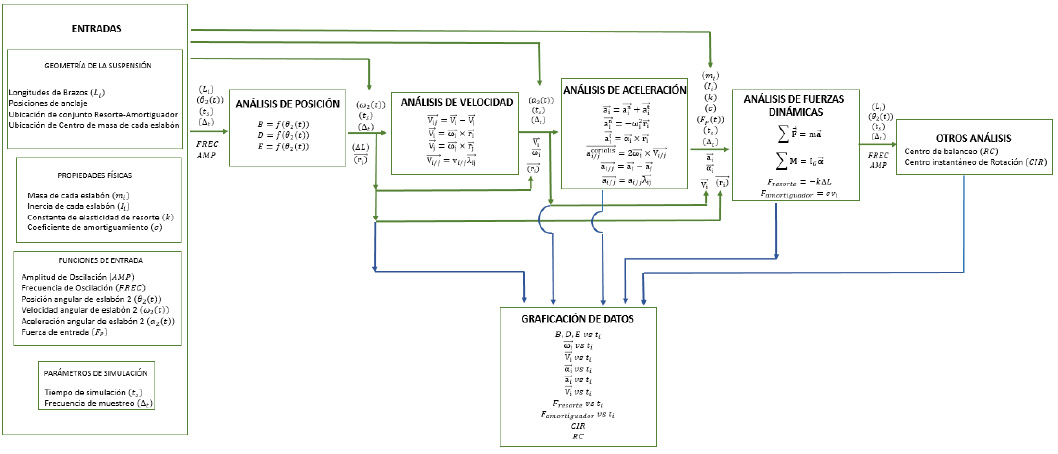
La programación del modelo teórico se basa en las ecuaciones desarrolladas (1-8), las cuales son implementadas y resueltas con el software Matlab. En la figura 9 se muestra un diagrama de bloques con el flujo de información que utiliza el programa desarrollado, para alcanzar resultados tabulados y gráficas de comportamiento de la suspensión objeto de estudio.
Desarrollo de un banco de pruebas de una suspensión
Con el propósito de obtener información experimental sobre las variables cinemáticas y dinámicas de una suspensión se diseña y construye un banco de ensayos. Este banco permite la ejecución de pruebas con distintas configuraciones de suspensiones independientes de tipo doble horquilla. Se pueden lograr varias configuraciones variando, por ejemplo, su geometría (dimensiones de los brazos de la suspensión y de la mangueta), dando como resultado el cambio del comportamiento dinámico de la suspensión. Para el presente estudio se emplean brazos de suspensión, inferior y superior, iguales y paralelos, pero el banco podría ensayarse con otras configuraciones. Además, es posible probar numerosas combinaciones del conjunto resorte-amortiguador, intercambiando este subsistema, así como los puntos de fijación en la suspensión.
Para cada tipo de terreno o distintas circunstancias de funcionamiento del sistema de suspensión del vehículo,
se tienen diferentes amplitudes y frecuencias de oscilación. Además de ello, según Luna y Vallejo (2017), los valores
generales de amplitud de oscilación de una suspensión de vehículo se encuentran en torno a los 110 mm y recomienda para los ensayos controlados una frecuencia máxima de 20 Hz.
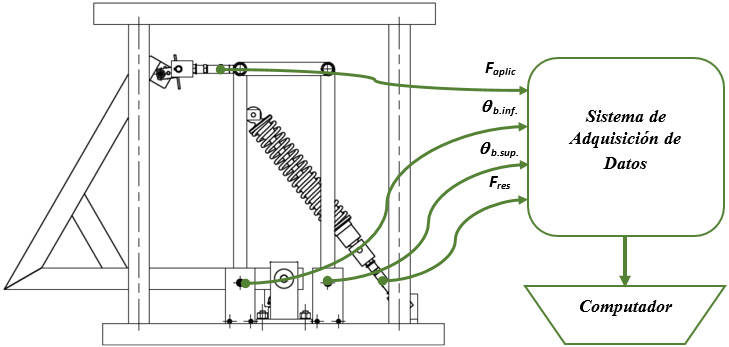
En la figura 10 se muestra la vista lateral de la instalación experimental, junto con un diagrama que aclara los puntos de medición y la conexión al sistema de adquisición de
datos. El banco de pruebas cuenta con la posibilidad
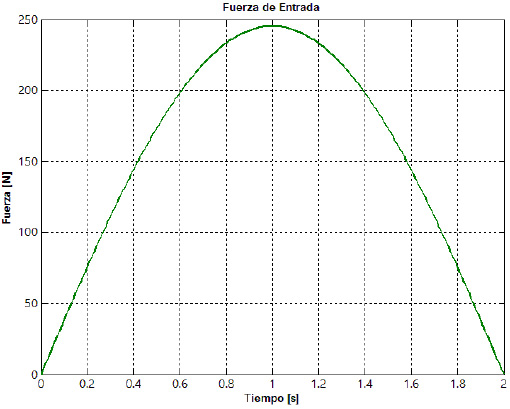
de manejar dos factores experimentales independientes: amplitud del recorrido y la frecuencia de la oscilación. El primero de ellos puede ajustarse en un rango de 0 – 127 mm y el segundo en un rango de 0 – 10 Hz, respectivamente. Sin embargo, este rango de frecuencias que se reporta es general, descrito por varios autores para una amplia gama de suspensiones y vehículos. En la presente investigación se decidió experimentar con los dos niveles de frecuencia que se muestran en la tabla 3, fundamental-mente para comprobar la resolución de la instrumen-tación implementada en la instalación experimental; si es capaz de encontrar diferencias en el funcionamiento, para valores relativamente cercanos de frecuencias de aplicación de carga, lo hará también para frecuencias aplicadas más alejadas entre sí. Las frecuencias utilizadas serían propias de un vehículo desplazándose por un terreno ondulado o baja/moderada velocidad. La magnitud de la fuerza aplicada en función del tiempo que se utiliza para validar el modelo teórico (véase figura 13) responde a las fuerzas que el banco experimental es capaz de soportar con seguridad. Igual que en el caso de la frecuencia, esta función de fuerza aplicada es consistente con las cargas que experimentaría una suspensión de vehículo monoplaza ligero.
Tabla 3. Niveles para los factores independientes del diseño de experimentos
|
Factor |
Nivel inferior |
Nivel superior |
|
Amplitud [mm] |
35 |
127 |
|
Frecuencia [Hz] |
0,5 |
1,0 |
Debido a las condiciones de operación que se quieren estudiar, el diseño experimental es basado en un arreglo factorial completo, de dos factores con dos niveles cada uno. Este tipo de diseño permite el estudio del efecto conjunto de los factores amplitud y frecuencia del movimiento sobre las respuestas dinámicas de la suspensión.
El sistema de medición consta de cuatro puntos de medición, dos de ellos son celdas de carga, la primera ubicada en la entrada del sistema (mangueta) y la segunda en el conjunto resorte-amortiguador. Los otros dos sensores son potenciómetros calibrados para medir la posición angular de cada brazo de la suspensión. La información de los sensores es procesada con el software LabView y su registro es almacenado en un archivo tipo .xls. La señal de los cuatro sensores se toma a una frecuencia de muestreo de 15 Hz. Además, el sistema de medición cuenta con una calibración previa mediante software para minimizar el error de medición. La información medida es registrada y es útil para determinar el comportamiento en función del ti-
empo de la fuerza aplicada a la suspensión, fuerza en el resorte, fuerza en el amortiguador, posición angular, velocidad y aceleración angulares de los brazos de la suspensión.
Se necesita contar con la caracterización del conjunto resorte-amortiguador por medio de pruebas de movimiento cíclico. Se hacen dos tipos de ensayos, el primero
para el conjunto resorte-amortiguador y el segundo
solo para el amortiguador. Para el primer ensayo, se aplica una carga de compresión sobre el conjunto resorte-amortiguador de 0 a 1 kN, a una velocidad de 100 mm/s. Para esto se emplea una máquina universal de ensayos marca Shimadzu referencia AGX PLUS 300 kN. Los resultados de esta caracterización se muestran en la figura 11. En el diagrama de carga contra desplazamiento se aprecian dos segmentos: el primer segmento corresponde al primer ciclo del ensayo donde es necesario que la máquina de ensayos supere la inercia propia del componente, por ende, su deformación es mayor, así como la fuerza ejercida; el segundo segmento, así como los ciclos posteriores, corresponde a un comportamiento estable, donde se evidencian los recorridos de acortamiento (bump) y alargamiento (rebound); para el primero de ellos es necesario aplicar más fuerza, debido a las especificaciones técnicas incorporadas en este componente de la suspensión.
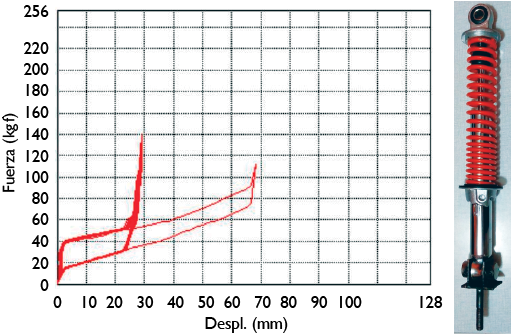
Figura 11. Curva de comportamiento para el conjunto resorte-
amortiguador
Para el segundo ensayo, se aplicó de nuevo un movimiento cíclico, pero ahora solo sobre el amortiguador (el resorte fue removido). La figura 12 muestra la fuerza ejercida en los recorridos de acortamiento (bump) y alargamiento (rebound) en función del desplazamiento (el primero de ellos con una fuerza mayor). Este segundo ensayo se hizo con las mismas condiciones del primero.
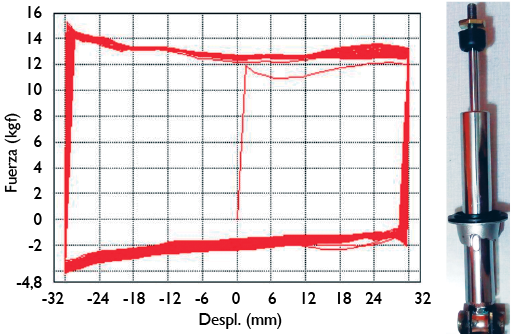
Figura 12. Curva de caracterización para el amortiguador
Con la información suministrada por estos dos ensayos fue posible caracterizar al conjunto resorte-amortiguador, obteniéndose la constante de rigidez elástica y los coeficientes de amortiguamiento en los recorridos de acortamiento y alargamiento, respectivamente.
Resultados
Resultados para el modelo teórico
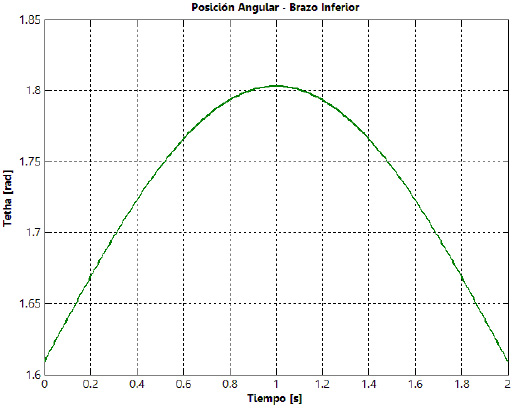
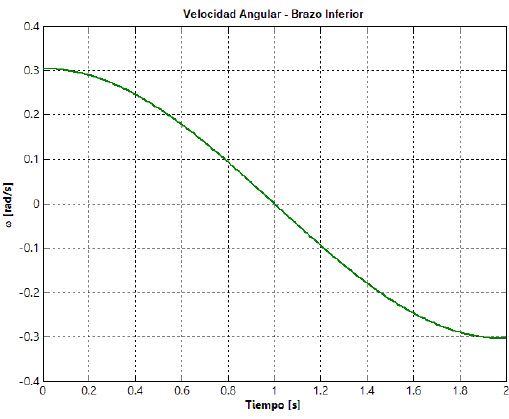
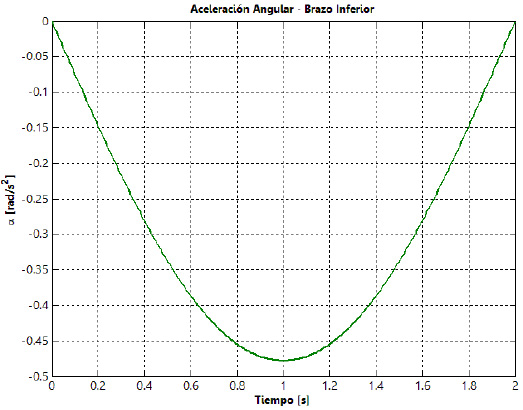
En la figura 13 se muestran las curvas de posición, velocidad y aceleración angulares del eslabón 2 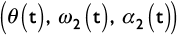 , así como la fuerza de entrada (
, así como la fuerza de entrada (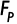 ) a la suspensión. Las curvas son obtenidas para una condición de bache sobre el pavimento con perfil sinusoidal, con una única repetición.
) a la suspensión. Las curvas son obtenidas para una condición de bache sobre el pavimento con perfil sinusoidal, con una única repetición.
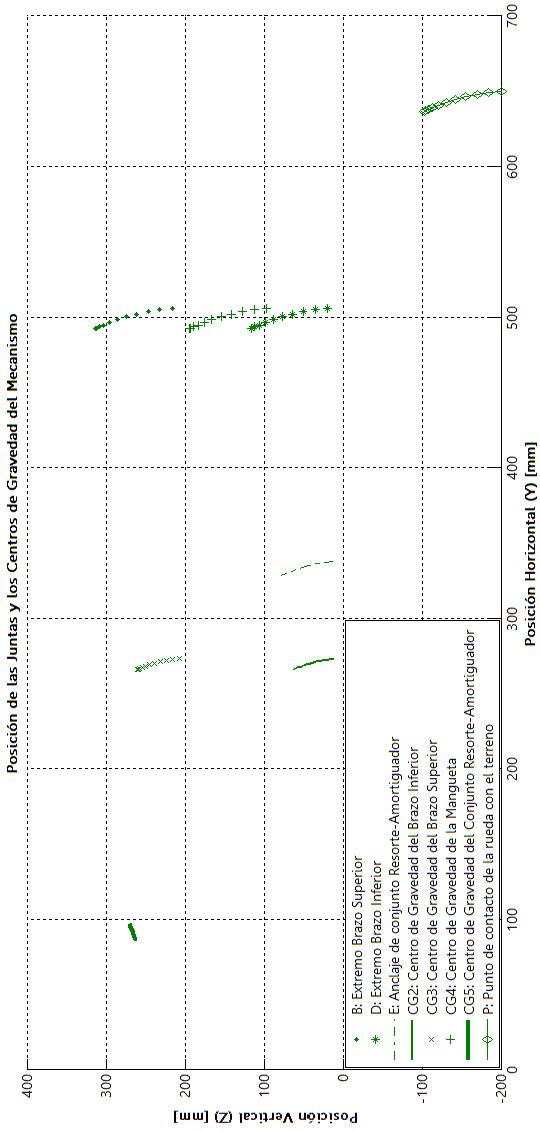
Las trayectorias que experimentan las juntas, centros de masa y el punto medio de la rueda con el suelo, es un resultado de importancia en el diseño y análisis del comportamiento de una suspensión. En la figura 14 se muestra
el movimiento de los puntos de interés cinemático sobre la configuración geométrica con la cual se realizaron las pruebas experimentales. Es de notar el recorrido pequeño que realiza el centro de masa del conjunto resorte-amortiguador. En el presente estudio se definió una ecuación de comportamiento del momento de inercia principal másico para este conjunto en función de su elongación. No obstante, se encuentra que la influencia de la variación del momento de inercia efectivo de este componente sobre la dinámica de la suspensión resulta insignificante.
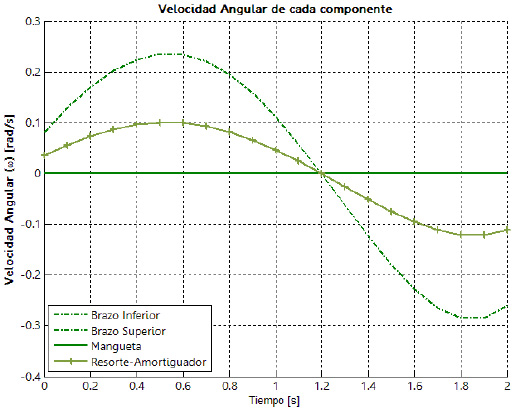
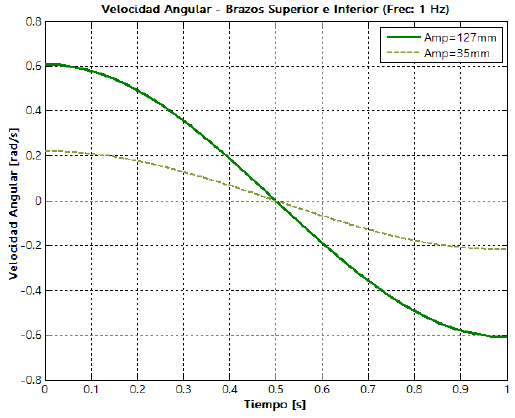
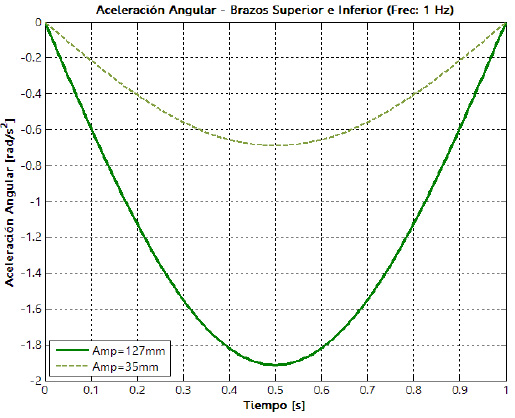
Las velocidades y aceleraciones angulares que experimentan los eslabones principales de la suspensión son calculadas resolviendo el sistema de ecuaciones obtenidas del análisis cinemático. Las curvas mostradas en la figura 15, corresponden a las velocidades y aceleraciones angulares de cada uno de los elementos que integran el sistema de
suspensión; estas curvas muestran el comportamiento para una amplitud de oscilación de 127 mm y una frecuencia de 0,5 Hz. La cinemática de ambos brazos, inferior y superior, coincide debido a que son iguales y paralelos, pero esto en general no es así. Estos resultados pueden contrastarse con los datos obtenidos mediante experimentación.
Para realizar el estudio de los factores independientes de
amplitud y frecuencia se usa una función de posición
de entrada senoidal mostrada en la figura 13, dado que al ser una función periódica suave permite observar
de una mejor manera el comportamiento de las diferentes variables dependientes.
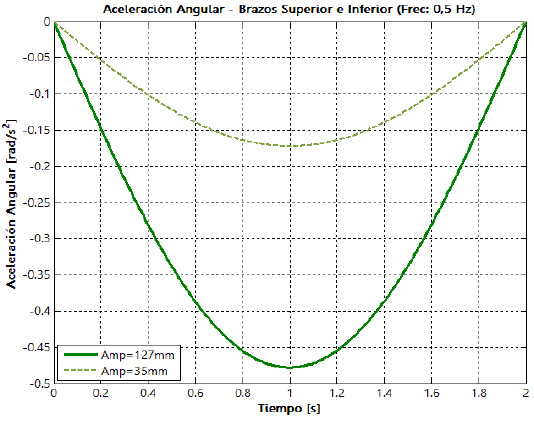
En las figuras 16 y 17 se muestra el comportamiento de la velocidad y aceleración angulares de los brazos superior e inferior, para los dos niveles de la amplitud de la oscilación y los dos niveles de frecuencia, respectivamente.
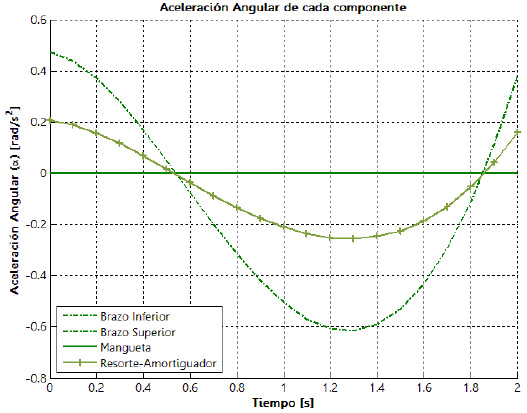
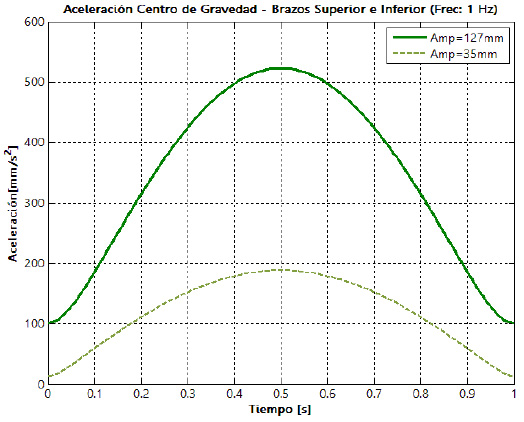
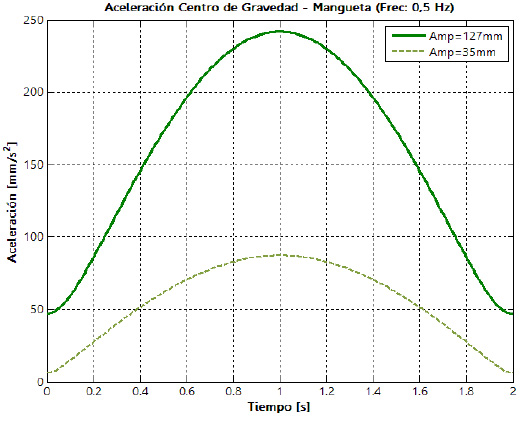
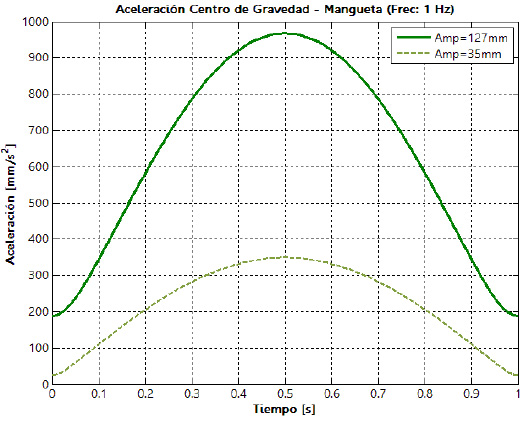
También se obtienen las aceleraciones lineales, componente horizontal, componente vertical y resultante, que experimentan cada una de los pares cinemáticos y los centros de masa de los eslabones que conforman la suspensión. En la figura 18 se muestra el comportamiento de las aceleraciones de los centros de masa del brazo inferior (a) y de la mangueta (b), respectivamente, para los dos niveles de la amplitud de la oscilación y los dos niveles de frecuencia.
Luego de definir la cinemática del mecanismo de la suspensión se obtienen los resultados para el comportamiento dinámico. Por medio de la solución del modelo cinético es posible encontrar las fuerzas sobre cada uno de los pares cinemáticos, así como sobre el conjunto resorte-
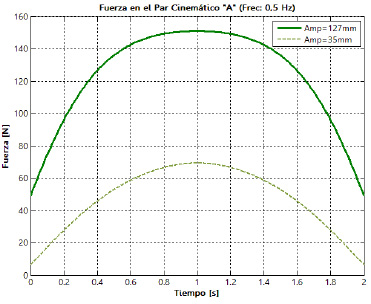
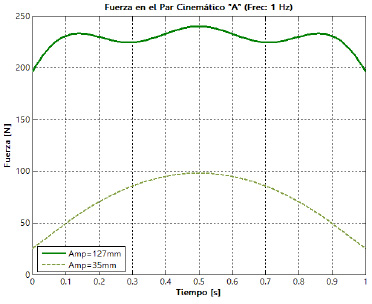
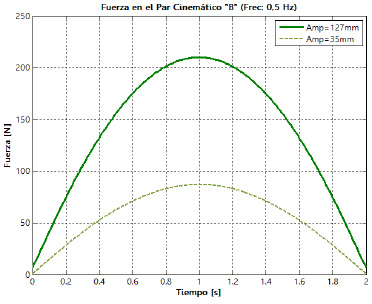
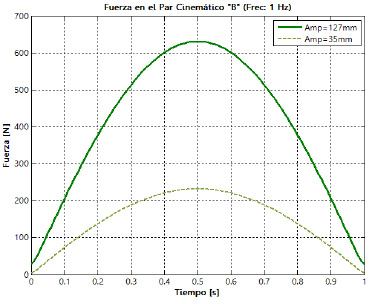
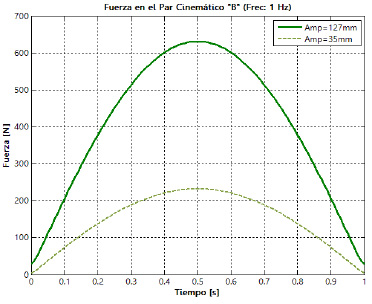
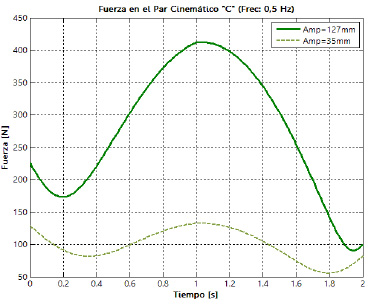
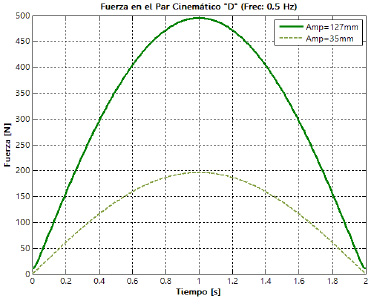
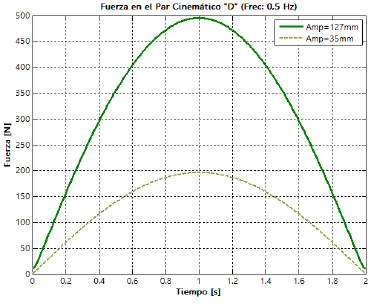
amortiguador. En la figura 19 es posible apreciar la evolución de las fuerzas resultantes sobre las cuatro juntas que posee la suspensión, para los dos niveles de la amplitud de la oscilación y los dos niveles de frecuencia definidos. Las letras empleadas para la identificación de las juntas se corresponden con las presentadas previamente en la figura 7.
Se muestra en la figura 20 el comportamiento de las fuerzas que actúan sobre los elementos que componen el conjunto resorte-amortiguador. Se puede apreciar que actúa sobre el conjunto resorte-amortiguador una precarga de 85 N, la cual provoca una deformación inicial y el consiguiente prehundimiento del componente elástico y el amortiguador, respectivamente.
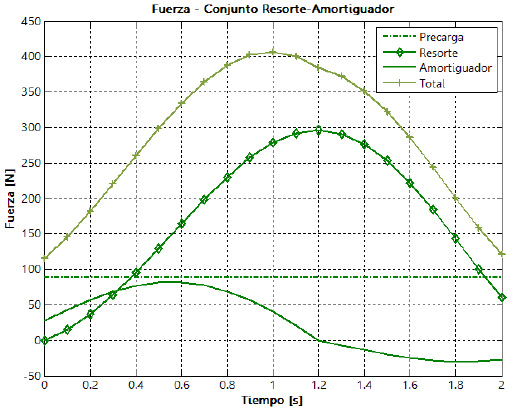
Figura 20. Fuerzas en los elementos del conjunto resorte-amortiguador para una amplitud de 127 mm y una frecuencia de 0,5 Hz
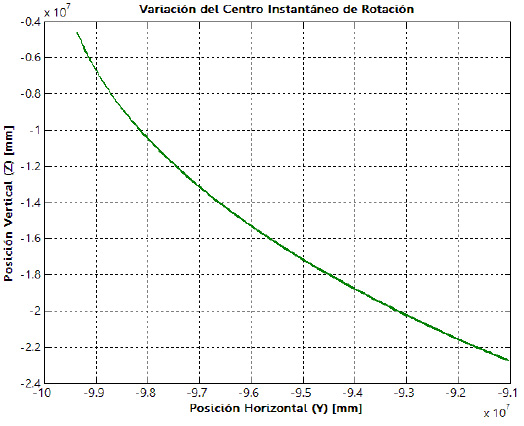
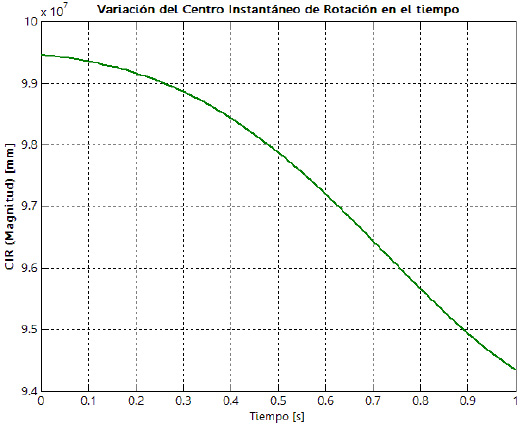
Como parámetros cinemáticos importantes en el estudio de la suspensión sobre el modelo matemático, se obtiene el comportamiento tanto en el tiempo como en el espacio del centro instantáneo de rotación (CIR) y centro de balanceo (RC). En la figura 21 aparece, tanto la evolución del recorrido como el cambio de magnitud en función del tiempo, del centro instantáneo de rotación para la suspensión bajo estudio.
Finalmente, en la figura 22 se muestra el comportamiento del centro de balanceo para la suspensión bajo estudio respecto al tiempo.
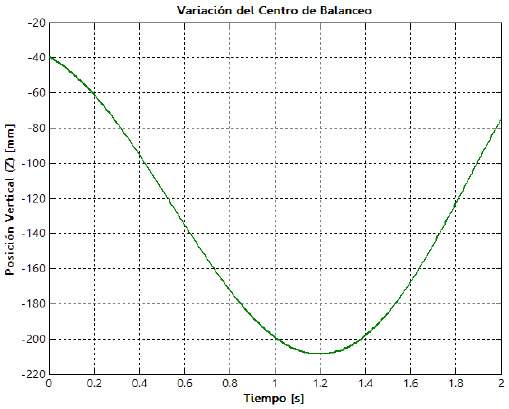
Figura 22. Variación del centro de balanceo respecto al tiempo
Resultados experimentales
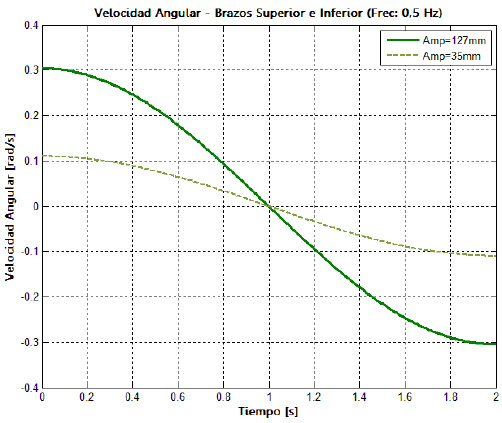
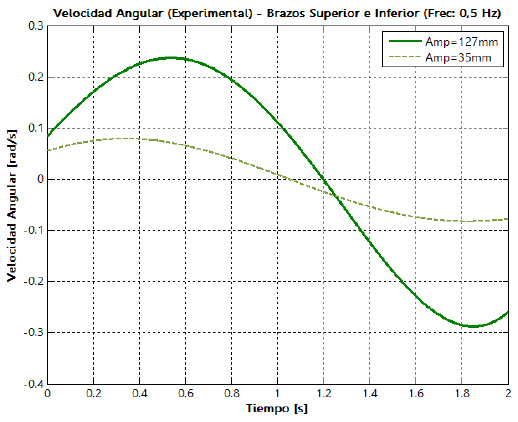
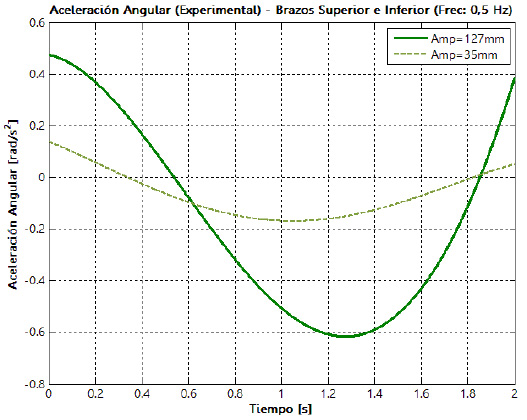
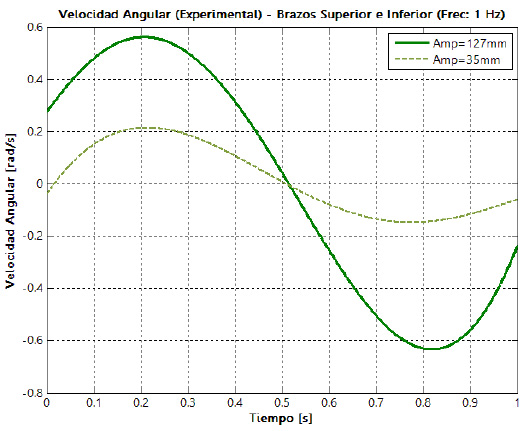
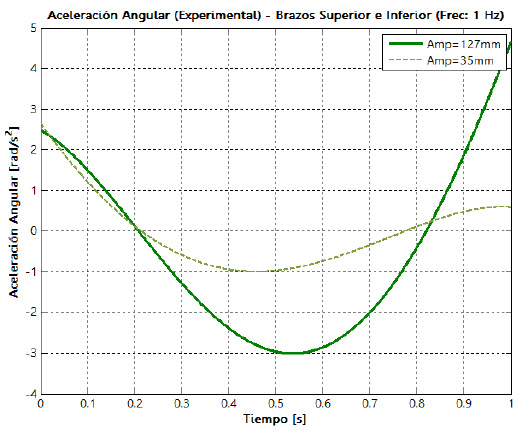
Los datos de posición angular obtenidos con ayuda de la instalación experimental son utilizados para calcular las funciones de velocidad y aceleración angular de cada uno de los eslabones de la suspensión. En las figuras 23 y 24 aparecen las curvas de aceleración angular de los brazos superior e inferior, para los dos niveles de la amplitud de la oscilación y una frecuencia de 0,5 Hz.
En la figura 25 se aprecia el comportamiento de la fuerza resultante que experimenta el conjunto resorte-amortiguador, para un nivel de amplitud de oscilación de 127 mm y una frecuencia de oscilación de 0,5 Hz. Este conjunto se encuentra precargado para que el modelo experimental emule la situación real. Se resalta la importancia de que en el modelo experimental se tenga en cuenta el valor predefinido de la masa suspendida del vehículo.
Con los resultados de todas las réplicas realizadas para cada tratamiento experimental, se hizo la construcción de los gráficos de distribución de datos, con el propósito de
analizar tanto la dispersión como la tendencia de los
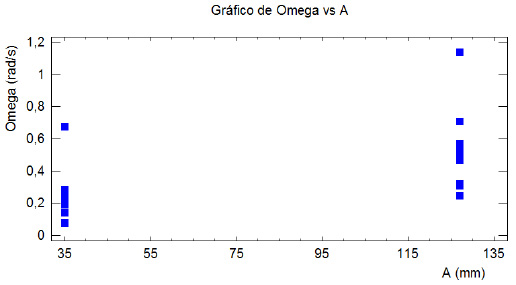
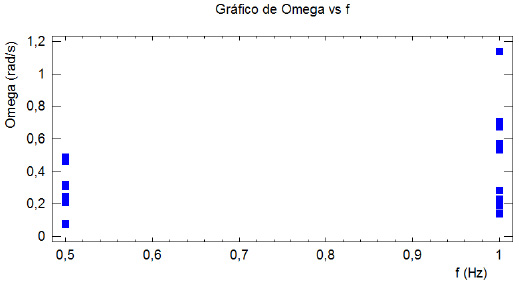
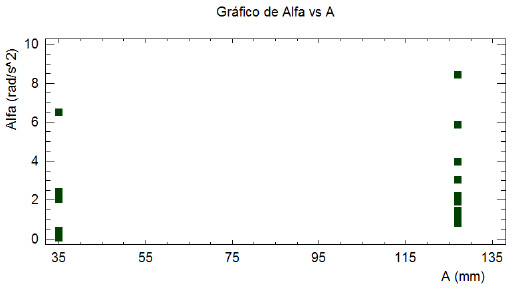
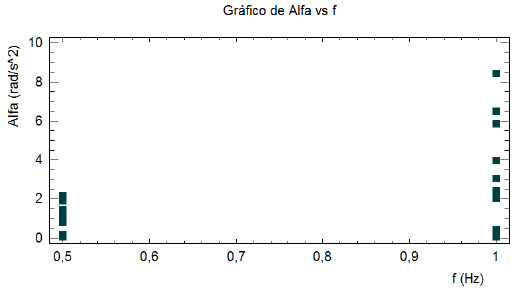
valores de acuerdo con los niveles de los factores amplitud y frecuencia de la oscilación (Mendoza & Bautista, n.d.; Montgomery, 2013). Los resultados para la velocidad angular máxima del brazo inferior se muestran en la figura 26 para: (a) amplitud de la oscilación y (b) frecuencia de la oscilación, respectivamente. Mientras que en la figura 27 se muestra la distribución de los datos experimentales para la aceleración angular máxima del brazo inferior para: (a) amplitud de la oscilación y (b) frecuencia de la oscilación, respectivamente.
Figura 25. Fuerza resultante en el conjunto resorte-amortiguador (datos experimentales)
De manera similar resulta fundamental analizar el comportamiento de las fuerzas que actúan sobre los componentes principales de la suspensión de un vehículo ligero desplazándose por un terreno ondulado a baja o moderada
velocidad. En la figura 28 se muestra el comportamiento de la fuerza pico aplicada sobre la suspensión en función de
la amplitud y de la frecuencia de la oscilación, de acuerdo con el espacio experimental definido.
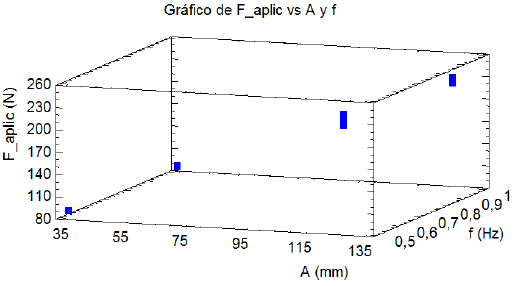
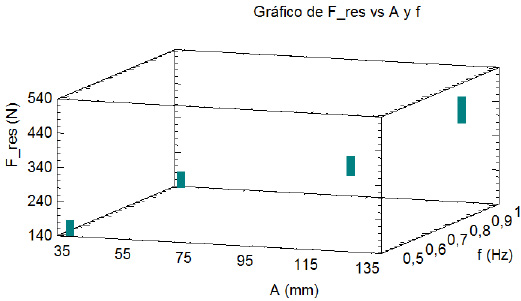
Figura 28. Fuerza pico aplicada a la suspensión en función de la amplitud y la frecuencia de oscilación
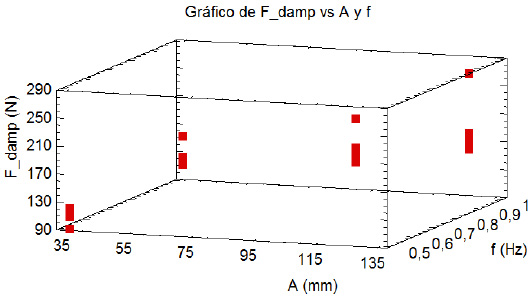
Por último, en la figura 29 aparecen los comportamientos de las fuerzas máximas ejercidas por el resorte (a) y el amortiguador (b), respectivamente, en función de la amplitud y la frecuencia de la oscilación, de acuerdo con el arreglo experimental definido.
Discusión
El comportamiento de la posición, velocidad y aceleración angulares del brazo inferior descritas por el modelo teórico es similar al encontrado con las señales cinemáticas de entrada (posición angular y sus dos primeras derivadas) del
modelo físico. Esto se corrobora con los porcentajes
de variación límite, los cuales para la velocidad angular no exceden en ningún caso el 16% y para la aceleración angular no superan el 27%.
El movimiento del centro de gravedad del conjunto
resorte-amortiguador es muy leve, ya que la amplitud de oscilación en términos generales no es muy alta.
Se demuestra que la variación del momento principal de
inercia del conjunto resorte-amortiguador es muy
pequeña, provocando un efecto despreciable en el comportamiento dinámico de la suspensión. También se observa que la aceleración de menor magnitud para la suspensión se encuentra en el conjunto resorte-
amortiguador, esto se debe a que es muy leve el movimiento rotacional de este componente.
El comportamiento de las fuerzas sobre cada uno de los pares cinemáticos del sistema de suspensión evidencia que sobre el brazo inferior se encuentran las mayores cargas, debido a que este componente es quien transmite
las cargas al conjunto resorte-amortiguador y en gran parte hacia el chasis.
Respecto al conjunto resorte-amortiguador, se observa que el resorte posee un comportamiento lineal con la deformación, dado que en el rango de operación ninguna espira alcanza a cerrarse. Por su parte, el amortiguador experimenta comportamientos distintos en los movimientos de compresión y extensión. El comportamiento de la fuerza en el conjunto resorte-amortiguador es
típico; se comprueba que el resorte ejerce comparativamente
mayor fuerza, para las condiciones de amplitud y frecuencia estudiadas. El conjunto cumple con su función de atenuar la oscilación, además de disipar gran parte de la energía, que de otro modo sería transferida al chasis. Sin embargo, el comportamiento de la curva para la fuerza resultante teórica difiere un poco de la descrita por el modelo físico, aunque las formas son muy parecidas y los instantes en que se alcanzan los niveles extremos también prácticamente coinciden. En la figura 30 se muestran los valores de la fuerza resultante, niveles máximos y mínimos, alcanzados por los modelos teóricos y físicos, respectivamente. El porcentaje de variación entre ambos modelos es aceptable para valores altos de la fuerza sobre el conjunto resorte-amortiguador, pero en el rango bajo de esta fuerza el porcentaje de variación supera
el 50%. Lo anterior es producto a la combinación de dos situaciones que acentúan el porcentaje de variación para valores
bajos de la fuerza resultante. En primer lugar, la ligera
diferencia entre la cinemática ideal (teórica) y la real que se genera en el banco de ensayos, provoca desviaciones entre los resultados para la deformación del resorte y la velocidad sobre el amortiguador; en segundo lugar, las pérdidas mecánicas (por ejemplo, los rozamientos en los
pares cinemáticos) tienen mayor peso relativo para
los valores de fuerzas que se miden.
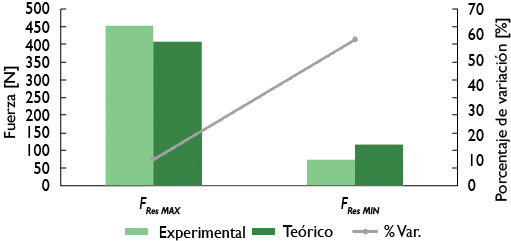
Figura 30. Comparación de la fuerza resultante sobre el conjunto resorte-amortiguador entre el modelo teórico y el experimental para valores máximos y mínimos
Las curvas de velocidad y aceleración angulares tienen el mismo comportamiento, sin importar los niveles de amplitud y frecuencia de la oscilación, las diferencias se
observan en las magnitudes pico que se alcanzan. Al cambiar la amplitud de la oscilación del nivel inferior al
superior y manteniendo la frecuencia constante, se aprecia un incremento en la velocidad angular de las barras de alrededor de 250%. Sin embargo, un cambio significativo se observa cuando se incrementa la frecuencia de oscilación del nivel inferior al superior en un factor de dos para una amplitud constante, ya que la velocidad angular de las barras incrementa su magnitud de forma proporcional a este factor experimental. Para la aceleración ocurre algo similar al cambiar el factor experimental de amplitud de la
oscilación. Sin embargo, debe resaltarse que, al cambiar la frecuencia en un factor de dos, las aceleraciones como las velocidades ya no tienden a incrementarse sobre este mismo factor, sino en cuatro veces, pasando así de una aceleración angular de  para una frecuencia de 0,5 Hz, a
para una frecuencia de 0,5 Hz, a  para una frecuencia de 1,0 Hz.
para una frecuencia de 1,0 Hz.
Si bien se encontraron factores de proporción entre las velocidades y aceleraciones con relación a la frecuencia y la amplitud de la oscilación, las fuerzas sobre los pares cinemáticos no tienen de una forma clara un mismo factor; aunque sí se evidencia que el factor experimental de mayor influencia sobre la magnitud de las fuerzas en los pares cinemáticos es la frecuencia de oscilación; este factor logra el incremento sustancial de cada fuerza en cada par sobre una misma amplitud de oscilación, en este caso para los valores de fuerza dados en el desarrollo experimental de esta investigación.
La fuerza elástica del resorte no se encuentra afectada por
la frecuencia de oscilación, ya que la fuerza ejercida
por este componente solo depende del desplazamiento que ocurra linealmente sobre su propio eje de simetría. En cambio, la fuerza de amortiguación sí es dependiente de la velocidad del émbolo, por lo que se aprecia que, a mayor frecuencia de oscilación, se incrementa esta fuerza. Por ello, cuando la frecuencia pasa del nivel inferior al superior la fuerza de amortiguación se incrementa en 100%.
Los resultados obtenidos por medio del modelo teórico desarrollado muestran un comportamiento similar cuando se comparan con las curvas obtenidas experimentalmente, así como la tendencia de los resultados obtenidos con el diseño experimental. La variación entre las curvas teóricas y las experimentales se debe a la función de entrada en el banco de pruebas que es aproximadamente senoidal, a la generación de pequeñas perturbaciones en el mecanismo generador del movimiento en el banco de ensayo y a errores propios del sistema de adquisición de datos.
Se evidencia que el factor que más afecta al comportamiento de la suspensión de un vehículo es la frecuencia de oscilación, representada en condiciones reales como la combinación entre la velocidad lineal del vehículo y el periodo de la ondulación de la vía. A mayor velocidad, para una misma amplitud, las magnitudes de las velocidades, aceleraciones y fuerzas en los pares cinemáticos del mecanismo se incrementan. El factor de amplitud de la oscilación depende más de las condiciones del terreno y la aplicación específica del vehículo.
Los parámetros del centro instantáneo de rotación y del centro de balanceo son fundamentales para el estudio y el diseño de una suspensión. En las curvas obtenidas se observa un comportamiento adecuado de estos parámetros. Un factor geométrico que aporta a lo anterior, es el hecho de contar con brazos iguales y paralelos, por lo que la intersección de la prolongación de estos no ocurre en teoría. Además, el centro de balanceo se ubica por debajo del plano de referencia que es el terreno, teniendo su máxima variación sobre el punto máximo de compresión de la suspensión (bump).
En los gráficos de distribución de datos, se observa que la dispersión de los valores de fuerza en cada elemento del conjunto resorte-amortiguador, así como en los valores de la fuerza aplicada no es muy alta. Sin embargo, la dispersión para los valores de velocidad y aceleración angular pico de los brazos de la suspensión sí resulta algo alta. Una de las causas de esta dispersión observada podría deberse a que el sistema de medición de la posición angular de cada brazo de suspensión tiene una frecuencia de muestreo máxima de 15 datos por segundos, lo cual puede resultar algo baja. Se recomienda como trabajo futuro el mejoramiento del sistema de medición en cuanto al incremento de la frecuencia de muestreo.
El modelo teórico no posee limitaciones para los niveles de los parámetros físicos involucrados o de escalado dimensional, aunque los resultados requerirían de validación experimental. Por lo que el modelo puede alimentarse con información de entrada de otros tipos de configuración para suspensión de doble horquilla y condiciones de operación, obteniendo así los resultados correspondientes.
Conclusiones
El presente trabajo de investigación estuvo enfocado al análisis cinemático y cinético de una suspensión de vehículo independiente de doble horquilla. Con base en los objetivos propuestos se pueden enunciar las siguientes conclusiones:
El programa realizado con el software Matlab queda comprobado con la revisión de varios casos típicos y los resultados obtenidos en el banco experimental. Este programa muestra ser versátil y flexible, y permite realizar el procedimiento de análisis en dos dimensiones de este tipo de suspensiones, teniendo como entradas la geometría y un conjunto de propiedades mecánicas de sus componentes.
El diseño experimental implementado fue de gran importancia para la validación de los resultados obtenidos con el modelo matemático; se evidencia la tendencia de los datos frente a distintos niveles de amplitud y frecuencia de oscilación, obteniendo curvas características para cada uno de los componentes del sistema de suspensión.
Como primer modelo teórico propuesto los resultados son favorables, teniendo en cuenta su gran flexibilidad en cuanto a cantidad de parámetros de la suspensión que
pueden definirse, donde se pueden modificar las masas, inercias, longitudes y posiciones iniciales de cada componente del sistema de suspensión, así como las constantes de rigidez y amortiguamiento del conjunto resorte-amortiguador.
Por otro lado, las variables de entrada pueden modificarse a gusto del usuario, teniendo en cuenta que los parámetros fundamentales de amplitud y frecuencia de la
oscilación emulan las condiciones reales sobre el terreno en el que el vehículo se desplaza, esencialmente el perfil geométrico del terreno y la velocidad del vehículo.
La metodología propuesta para los análisis de la suspensión a la luz del modelo teórico permite la modificación rápida de los parámetros de entrada, logrando así un
primer acercamiento de forma sencilla a sistemas de
suspensión existentes y modificaciones planteadas previamente que se deseen realizar, sin tener que recurrir en primera instancia a la experimentación.
Se deberá desarrollar un modelo de vibraciones para el sistema mecánico existente, que considere las frecuencias naturales y formas modales del sistema. Con el cual se puedan estudiar las respuestas de cada elemento a las condiciones de entrada dadas por el usuario y comprobar el desempeño de la suspensión ante este fenómeno. A
futuro, podrían implementarse en la instalación experimental un conjunto de acelerómetros, con el fin de
estudiar la influencia de los factores experimentales en el comportamiento vibracional de los componentes que constituyen la suspensión del vehículo.
Referencias
Blundell, M., & Harty, D. (2014). The multibody systems approach to vehicle dynamics. Oxford: Elsevier Butterworth-Heinemann.
Buitrago, É. (2011). Diseño del sistema de suspensión de un vehículo monoplaza tipo fórmula Sena. Medellín, Colombia: Universidad Nacional de Colombia, Facultad de Minas.
Datte, P., & Ross, J. S. (2016). About the preliminary design of the suspension spring and shock absorber. http://dx.doi.org/10.1088/1757-899X/147/1/012128
Dixon, J. C. (2009). Suspension geometry and computation. West Sussex: John Wiley and Sons Ltd.
Giovanny-Pablo, P. Q. (2012). Estudio cinemático del comportamiento de la suspensión de un prototipo de fórmula SAE Student Eléctrico del equipo UPM Racing. Madrid: Universidad Politécnica de Madrid.
Güler, D. (2006). Dynamic analysis of double wishbone suspension. School of Engineering and Sciences of Izmir Institute of Technology.
ISO 8855. Road vehicles – Vehicle dynamics and road-holding ability – Vocabulary, ISO § (2011). http://dx.doi.org/10.1109/ieeestd.2010.5733835
Luna-Pasquel, B. A., & Vallejo-Tito, J. A. (2017). Diseño, construcción e implementación de un banco de pruebas para el análisis de amortiguadores y muelles del sistema de suspensión de un vehículo. Ibarra, Ecuador: Universidad Técnica del Norte.
Mantilla-Nova, D. (2014). Diseño óptimo de resortes tipo ballesta para la suspensión de un vehículo comercial considerando las condiciones dinámicas. Bogotá: Universidad Nacional de Colombia. Recuperado de http://www.bdigital.unal.edu.co/49812/.
Mendoza, H., & Bautista, G. (n.d.). Diseño experimental. Recuperado el 1º de abril de 2018, de http://168.176.60.11/cursos/ciencias/2000352/index.html.
Montgomery, D. (2013). Diseño y análisis de experimentos. México: LIMUSA, S.A.
Morello, L., Genta, G., Cavallino, F., & Filtri, L. (2014). The motor car: Past, present and future. British Medical Journal (vol. 2). Torino: Springer Science & Business Media. http://dx.doi.org/10.1109/ieeestd.2010.5733835
Norton, R. L. (2013). Diseño de maquinaria. Massachusetts: McGraw-Hill Educación.
Rojas, G., & Arzola, N. (2013). Análisis del comportamiento dinámico de un vehículo con suspensión independiente tipo paralelogramo deformable y barras de estabilidad transversal. Revista Facultad de Ingeniería, (67), 112-125.
Sanz-Celada, F. (2015). Análisis del sistema de dirección de un automóvil mediante Multibody de Simulink. Recuperado de http://hdl.handle.net/10016/25331%0ADescargado.
Schommer, A., Soliman, P., Farias, L. T., & Martins, M. (2015). Analysis of a formula SAE vehicle suspension: Chassis. http://dx.doi.org/10.4271/2015-36-0275
Tanik, E., & Parlaktaş, V. (2015). On the analysis of double wishbone suspension. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 9(3), 1-10. http://dx.doi.org/10.1299/jamdsm.2015jamdsm0037
Thacker, S. (2015). Research paper on design and analysis double wishbone suspension system using finite element analysis. Recuperado de https://pdfs.semanticscholar.org/aedf/7ceb000bc8e65eb814496f448802ac3c69d5.pdf.
Thakare, S. A., Antapurkar, P. C., Shah, D. S., Dhamangaonkar, P. R., & Sapali, S. N. (2015). Design and analysis of modified front double wishbone suspension for a three wheel hybrid vehicle. Recuperado de https://www.longdom.org/proceedings/design-and-analysis-of-modified-front-double-wishbone-suspension-for-a-three-wheel-hybrid-vehicle-4667.html.
Vega, W. H., Llanes-Cedeño, E. A., & Molina, J. V. (2018). Review of the modeling and optimization characteristics for the design of the Macpherson suspension system. Recuperado de https://www.researchgate.net/publication/328769993_Review_of_the_Modeling_and_Optimization_Characteristics_for_the_Design_of_the_Macpherson_Suspension_System.
Yu, M., Evangelou, S. A., & Dini, D. (2017). Model identification and control for a quarter car test rig of series active variable geometry suspension. IFAC-PapersOnLine, 50(1), 3376-3381. http://dx.doi.org/10.1016/j.ifacol.2017.08.529