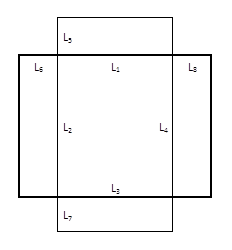Evaluation
of incident radiation by a V-Concentration System (VCS) in Bogotá, D.C.*
Evaluación de la radiación incidente por un sistema de
concentración en V (SCV) en Bogotá, D.C.*
Avaliação da radiação incidente por um sistema de
concentração V (VCS) em Bogotá, D.C. *
Carlos Augusto Bermúdez Figueroa **
Carlos Eduardo Tibavisco Delgado ***
Universidad de Cundinamarca
Date Received: January 01 of
2018
Date of Acceptance: March 03 of 2018
Publication Date: April 01, 2018
DOI: http://dx.doi.org/10.22335/rlct.v10i4.600
* The article result of the investigation ". Evaluation of incident radiation by a
V-Concentration System (VCS) in Bogotá, D.C." Universidad Cundinamarca.
** Master in Engineering with emphasis in Alternative Energies,
Universidad Libre, and researcher at the University of Cundinamarca, Colombia.
Affiliation: University of Cundinamarca. Email: carmetalbf@yahoo.es Orcid: https://orcid.org/0000-0002-6132-8195
*** Specialist in Telematics from Los Andes University, and researcher at
the University of Cundinamarca, Colombia. Affiliation: University of
Cundinamarca. Email: ctibavisco@hotmail.com Orcid: https://orcid.org/0000-0002-7496-4529
Abstract
The study presents the behavior of a V concentration system (VCS), as a
way to estimate the incident radiation on a flat surface, based on the solar
coordinates described in the equations of Spencer, J.W.
Increasing the areas of solar capture is a way to expand the solar radiation, captured on a flat surface by
reflection. Maximizing the fraction of solar radiation captured; for that
purpose, the V-Concentration System (VCS) was developed, adding four flat
mirror surfaces to a flat surface, each with an inclination
angle to the (flat) pickup surface. A statistical model was described to find a
regression and thus expose the specific behavior areas of reflection on the
(VCS), with the purpose of finding the optimal angle which achieves an increase
in the uptake of radiation on a flat surface.
Keywords: V-Concentration
System (VCS), Incident Radiation, Flat Surface, Solar Radiation, Reflection.
Resumen
Se
presenta un estudio para observar el comportamiento de un sistema de
concentración en V (SCV), como medio para estimar la radiación incidente sobre
una superficie plana, con base en las coordenadas solares descritas en las
ecuaciones de Spencer, J. W.
Aumentar
las áreas de captación solar es una forma para incrementar la radiación solar
capturada por una superficie plana por medio de la reflexión. Maximizando la
fracción de radicación solar captada; para tal propósito fue desarrollado el
sistema de concentración en V (SCV), que agrega cuatro superficies de espejos
planos a una superficie plana, cada una con un ángulo de inclinación respecto a
la superficie de captación (plana). De estos se elaboró un modelo estadístico
para encontrar una regresión y así exponer el comportamiento específico de las
áreas de reflexión del (SCV), con el propósito de encontrar el ángulo óptimo
que lograra un incremento en la captación de radiación sobre la superficie
plana.
Palabras clave: Sistema de
concentración en V (SCV), Radiación incidente, Superficie plana, Radiación
solar, Reflexión.
Resumo
Um
estudo é apresentado para observar o comportamento de um sistema de
concentração V (VCI), como um meio de estimar a radiação incidente em uma
superfície plana, com base nas coordenadas solares descritas nas equações de
Spencer, J. W.
Aumentar
as áreas de captação solar é uma forma de aumentar a radiação solar captada por
uma superfície plana por meio da reflexão. Maximizar a fração de radiação solar
capturada; Para este propósito, foi desenvolvido o sistema de concentração em V
(SCV), que adiciona quatro superfícies de espelhos planos a uma superfície
plana, cada uma com um ângulo de inclinação em relação à superfície de coleta
(plana). A partir deles, um modelo estatístico foi desenvolvido para encontrar
uma regressão e, assim, expor o comportamento específico das áreas de reflexão
(SCV), a fim de encontrar o ângulo ideal que alcançaria um aumento na captação
de radiação na superfície plana.
Palavras-chave:
V-Concentration System (SCV), Radiação incidente, Superfície plana, Radiação
solar, Reflexão.
Introduction
The main propose of the present
investigation is to show the behavior of a concentration system in V. At
estimating the capture of incident radiation on a flat surface, thorough the
reflection emitted by the inclined reflective surfaces (mirrors). The
methodology used for the development of the research
is shown in Figure 1.
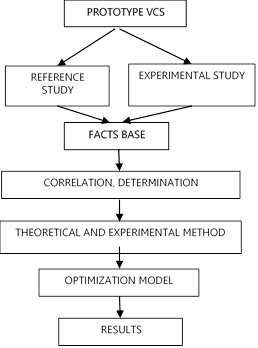
Figure 1. Research methodology. Source: Authors.
First, the prototype of the V-concentration system was
developed, which consists in adding four surfaces of flat mirrors to a flat
collection surface, at different angles of inclination and a certain height, in
order to collect experimental primary data.
Secondly, the mathematical calculation of reference was
developed, with the objective of obtaining the average daily and annual global
solar radiation of the system, based on mathematical methods provided by
Spencer, JW and the information of governmental
entities such as the Institute of Hydrology, Meteorology and Studies.
Environmental IDEAM, and the Mining and Energy Planning Unit (UPME).
Subsequently, a statistical model was made, which achieved
the best combination of the parameters that make up
the V-concentration system, based on the results obtained from the theoretical
and experimental calculation, the areas and angles of inclination of the
reflective surfaces.
Finally, the behavior of the reference model was evaluated and the experimental one with the radiation
obtained with the VCS.
Methodology
VCS Prototype
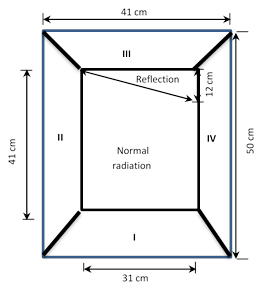
The prototype of the VCS consists in a flat surface and the
four reflecting surfaces as illustrated in Figure 2, and in Figure 3, the
prototype dimensions are shown. The aim of the
prototype is to expand the areas of solar incidence on the reflecting surfaces;
so by this mean the reflection on the flat surface would increase the solar
uptake.

Figure 2. VCS prototype
Source: Authors.
Figure 3a. VCS prototype dimensions
Source: Authors.
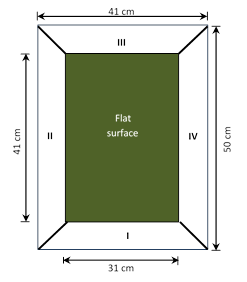
Figure 3b. VCS prototype dimensions
Source: Authors
Where:
I = Surface I
II = Surface II
III = Surface III
IV = Surface IV
β '= Angle by surface
Height reflective surfaces = 10 cm
Reference study
The objective of the reference study was
to calculate the total daily H (B) radiation captured by VCS, based on the
equations described by Spencer, in the solar Atlas, this information serves as
a basis to correlate with the experimental data, and thus to be able to pose
the model.
The objective of the reference study was
to calculate the total daily H (B) radiation captured by VCS, based on the
equations described by Spencer, in the solar Atlas, this information serves as
a basis to correlate with the experimental data, and thus to be able to pose
the model.
Experimental study
In days with direct irradiation in
Bogotá, experimental data were taken. The prototype was placed to the south
with a constant 5 ° inclination angle of the base surface in order to take
samples and photographs, the reflecting surfaces with variable angles: 15 °, 30
°, 45 ° and 60 °, hour by hour in order to observe the behavior of the
reflection, an example, is shown in Figure 4. It showed that the VCS forms different areas;
areas of shadows, which indicate that the incidence of solar rays on reflecting
surfaces is zero, areas of normal reflection, indicates that the incidence of
solar rays is perpendicular to the flat surface, data that is not taken into
account in the investigation and reflection areas that indicate the sun's rays
affect the reflective surfaces and reflect on the flat surface; this was
important data for the relevant database in the development of the model.
With the above information, the incident areas
were graphed and marked on the flat surface, in order to obtain a total
experimental H (β) radiation, the procedure was as
follows: the fractions of shadow areas are calculated, and the areas of
reflection, hour by hour, then the sum of the
fractions of calculated areas is elaborated, with the reference H (β)
obtained. Table 1 lists the results.

Figure 4. Reflection area at 8 am with angle 30 °
Source: Authors.
Table 1.
Global solar radiation of the system.
|
Inclination angle
(β)
|
Experimental
radiation H(β) (kWh/m2)
|
Theoretical radiation
H(β)
(kWh/m2)
|
|
0
|
3,880
|
3,82
|
|
15
|
3,882
|
3,81
|
|
30
|
4,180
|
3,76
|
|
45
|
3,879
|
3,68
|
|
60
|
4,336
|
3,57
|
|
15
|
3,858
|
3,81
|
|
30
|
4,364
|
3,76
|
|
45
|
4,001
|
3,68
|
|
60
|
4,434
|
3,57
|
Source: Authors.
Table 2.
Areas and angles of each surface, and Calculation of sines and cosines of each of the angles.
|
(β)
|
Areas (cm2)
|
Angles (°)
|
Cosines (rad)
|
Sines (rad)
|
|
Base
|
S1
|
S2
|
S3
|
S4
|
Base
|
S1
|
S2
|
S3
|
S4
|
Base
|
S1
|
S2
|
S3
|
S4
|
Base
|
S1
|
S2
|
S3
|
S4
|
|
0
|
1271
|
360
|
460
|
360
|
460
|
5
|
5
|
90
|
-5
|
-90
|
0,996
|
1,00
|
0,00
|
1,00
|
0,00
|
0,09
|
0,09
|
1,00
|
-0,09
|
-1,00
|
|
15
|
1271
|
360
|
460
|
360
|
460
|
5
|
20
|
75
|
-10
|
-75
|
0,996
|
0,94
|
0,26
|
0,98
|
0,26
|
0,09
|
0,34
|
0,97
|
-0,17
|
-0,97
|
|
30
|
1271
|
360
|
460
|
360
|
460
|
5
|
35
|
60
|
-25
|
-60
|
0,996
|
0,82
|
0,50
|
0,91
|
0,50
|
0,09
|
0,57
|
0,87
|
-0,42
|
-0,87
|
|
45
|
1271
|
360
|
460
|
360
|
460
|
5
|
50
|
45
|
-35
|
-45
|
0,996
|
0,64
|
0,71
|
0,82
|
0,71
|
0,09
|
0,77
|
0,71
|
-0,57
|
-0,71
|
|
60
|
1271
|
360
|
460
|
360
|
460
|
5
|
65
|
30
|
-55
|
-30
|
0,996
|
0,42
|
0,87
|
0,57
|
0,87
|
0,09
|
0,91
|
0,50
|
-0,82
|
-0,50
|
|
15
|
1271
|
360
|
460
|
360
|
460
|
5
|
20
|
75
|
-10
|
-85
|
0,996
|
0,94
|
0,26
|
0,98
|
0,09
|
0,09
|
0,34
|
0,97
|
-0,17
|
-1,00
|
|
30
|
1271
|
360
|
460
|
360
|
460
|
5
|
35
|
60
|
-25
|
-60
|
0,996
|
0,82
|
0,50
|
0,91
|
0,50
|
0,09
|
0,57
|
0,87
|
-0,42
|
-0,87
|
|
45
|
1271
|
360
|
460
|
360
|
460
|
5
|
50
|
45
|
-35
|
-45
|
0,996
|
0,64
|
0,71
|
0,82
|
0,71
|
0,09
|
0,77
|
0,71
|
-0,57
|
-0,71
|
|
60
|
1271
|
360
|
460
|
360
|
460
|
5
|
65
|
30
|
-55
|
-30
|
0,996
|
0,42
|
0,87
|
0,57
|
0,87
|
0,09
|
0,91
|
0,50
|
-0,82
|
-0,50
|
Source:
Authors.
Table 3.
Areas of reflection of the surfaces
|
(β)
|
Reflected area at the
cosine (cm2)
|
Reflected area at the
sine (cm2)
|
Captured energy (kWh/m2)
|
|
Base
|
SI
|
SII
|
SIII
|
SIV
|
Base
|
SI
|
SII
|
SIII
|
SIV
|
Theory
|
Experimental
|
|
0
|
1.266
|
359
|
0
|
359
|
0
|
111
|
31
|
460
|
-31
|
-460
|
3,82
|
3,880
|
|
15
|
1.266
|
338
|
119
|
355
|
119
|
111
|
123
|
444
|
-63
|
-444
|
3,81
|
3,882
|
|
30
|
1.266
|
295
|
230
|
326
|
230
|
111
|
206
|
398
|
-152
|
-398
|
3,76
|
4,180
|
|
45
|
1.266
|
231
|
325
|
295
|
325
|
111
|
276
|
325
|
-206
|
-325
|
3,68
|
3,879
|
|
60
|
1.266
|
152
|
398
|
206
|
398
|
111
|
326
|
230
|
-295
|
-230
|
3,57
|
4,336
|
|
15
|
1.266
|
338
|
119
|
355
|
40
|
111
|
123
|
444
|
-63
|
-458
|
3,81
|
3,858
|
|
30
|
1.266
|
295
|
230
|
326
|
230
|
111
|
206
|
398
|
-152
|
-398
|
3,76
|
4,364
|
|
45
|
1.266
|
231
|
325
|
295
|
325
|
111
|
276
|
325
|
-206
|
-325
|
3,68
|
4,001
|
|
60
|
1.266
|
152
|
398
|
206
|
398
|
111
|
326
|
230
|
-295
|
-230
|
3,57
|
4,434
|
Source: Authors.
In Table 1, it is exposed that the system presents a greater solar uptake
when the angle of inclination of the four reflecting surfaces is 60 °, obtaining an H (β) of
4.336 kWh / m2 and 4.434 kWh / m2 which indicates an increase in global
radiation compared to the reference value which corresponds
to 3.57 kWh / m2 at 60 °.
The areas of each surface with their respective angles of inclination
with respect to the flat surface are shown (Table
2). The sine and cosine of
the angles of each surface are calculated, data needed to realize the product
of the areas with the sines and cosines in order to find the reflection areas
of the surfaces with respect to the coordinates in
cosine and sine, match in Table 3.
The database results from Table 3. From these, reflective areas, (cm2), in cosine and sine and the theoretical and experimental energy captured (kWh/m2), the correspondence between the variables and their relevance to the effect of the reflected area to
propose a model.
Correlation coefficients.
The Pearson
correlation coefficient (named after Karl Pearson, who formulated it) is a measure used in
Statistics to calculate the degree of linear relationship between two random
variables, therefore, it is also known as the linear correlation coefficient.
The correlation coefficients are determined by
Excel. Among the following pairs of variables: the theoretical measure vs. the
experimental, the theoretical measure vs each of the areas reflected in cosine
and sine, as well as the experimental measure vs each of the areas reflected in
cosine and sinus, with the purpose to quantify the
proportion of resemblance (correlation) and explanatory (determination) between
the pair of variables, as shown in the matrix of Table 4 and 5.
The data design leads to a multicollinearity situation which means that there is a strong correlation between each pair
of variables mentioned above. For example, in Table 4, it is observed that the
correlation coefficient between the theoretical and experimental measure is
-0.66, which means that the experimental values go
in a direction opposite to the theoretical ones. When finding the coefficient
of determination, for the same pair of variables, in Table 5, it is 44% that is
to say that the behavior of the theoretical explains 44% of the experimental
information, therefore, each one has an independent
behavior 56%.
When
comparing the correlations between the experimental measure vs the projected
areas, from Table 4, it is identified that all have a value greater than 0.66,
that is to say that all the surfaces have some contribution or decrease in the
average value of the captured radiation measured experimentally, the above can
be evidenced, so that all have a coefficient of determination higher than 44%,
according to Table 5.
Table 4.
Correlation results
|
Correlations
|
Measure
|
Theoretical
|
Cosine
SI
|
Cosine
SII
|
Cosine
SIII
|
Cosine
SIV
|
Sine
SI
|
Sine
SII
|
Sine SIII
|
|
Theoretical
|
-0,66
|
|
|
|
|
|
|
|
|
|
Cosine SI
|
-0,67
|
1,00
|
|
|
|
|
|
|
|
|
Cosine SII
|
0,67
|
-0,93
|
-0,95
|
|
|
|
|
|
|
|
Cosine SIII
|
-0,72
|
0,99
|
0,98
|
-0,89
|
|
|
|
|
|
|
Cosine SIV
|
0,68
|
-0,93
|
-0,95
|
0,99
|
-0,88
|
|
|
|
|
|
Sine SI
|
0,67
|
-0,92
|
-0,95
|
1,00
|
-0,88
|
0,99
|
|
|
|
|
Sine SII
|
-0,66
|
1,00
|
1,00
|
-0,94
|
0,99
|
-0,93
|
-0,93
|
|
|
|
Sine SIII
|
-0,73
|
0,98
|
0,99
|
-0,98
|
0,96
|
-0,98
|
-0,97
|
0,98
|
|
|
Sine SIV
|
0,67
|
-1,00
|
-1,00
|
0,94
|
-0,98
|
0,94
|
0,93
|
-1,00
|
-0,98
|
Source: Authors.
Table 5.
Determination
results.
|
Determinations
|
Measure
|
Theoretical
ca
|
Cosine
SI
|
Cosine
SII
|
Cosine
SIII
|
Cosine
SIV
|
Sine
SI
|
Sine
SII
|
Sine
SIII
|
|
Theoretical
|
0,44
|
|
|
|
|
|
|
|
|
|
Cosine SI
|
0,45
|
1,00
|
|
|
|
|
|
|
|
|
Cosine SII
|
0,45
|
0,87
|
0,91
|
|
|
|
|
|
|
|
Cosine SIII
|
0,51
|
0,98
|
0,96
|
0,79
|
|
|
|
|
|
|
Cosine SIV
|
0,47
|
0,86
|
0,90
|
0,97
|
0,78
|
|
|
|
|
|
Sine SI
|
0,45
|
0,85
|
0,90
|
1,00
|
0,78
|
0,97
|
|
|
|
|
Sine SII
|
0,44
|
1,00
|
1,00
|
0,89
|
0,97
|
0,87
|
0,87
|
|
|
|
Sine SIII
|
0,53
|
0,95
|
0,97
|
0,96
|
0,91
|
0,95
|
0,95
|
0,96
|
|
|
Sin SIV
|
0,45
|
1,00
|
1,00
|
0,88
|
0,97
|
0,89
|
0,87
|
1,00
|
0,97
|
Source:
Authors.
The correlation between the theoretical
measure vs each one of the areas reflected in cosine and sine, of Table 4, is
higher than 92% and this is reflected in the coefficients of determination
above 85%, shown in Table 6, therefore, a high degree of correspondence is
identified between the reflective areas of the theoretical and experimental
studies. For this reason, a simple linear regression model is proposed.
Simple linear regression model.
|
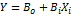
|
(1)
|
• 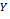 = Daily average, (kWh/m2), of solar radiation based on the variable
= Daily average, (kWh/m2), of solar radiation based on the variable
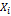
•  = coefficient, (kWh/m2), for the intercept of the data, based on
the surface of the base.
= coefficient, (kWh/m2), for the intercept of the data, based on
the surface of the base.
• 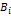 = estimated coefficient, (kWh/m4), of the contribution per square meter,
based on the projected surface.
= estimated coefficient, (kWh/m4), of the contribution per square meter,
based on the projected surface.
• Xi=
fixed term or intercept, corresponding
to the surface of the base or projected, m2.
Formulation of the
model.
For the construction of the specific
model for the case studied, it was necessary to obtain the coefficients (B),
that is a multiplicative factor, or constant number that is on the left
of a variable or unknown, and multiplies it, in order to determine the energy
captured by the VCS; by means of a statistical regression analysis in Excel,
with a confidence interval of 95%, of the theoretical and experimental measure
vs. the areas reflected in cosine and sine.
The summary of the models associated with
the experimental data and the theoretical data found are shown in Tables 6 and
7. The first column contains the area or variable of which we are speaking, it
is to remember that each area has a sine projection and another of cosine; the
next column (r) is the correlation coefficient, indicates the similarity by
projection; then the coefficient of determination follows (r^2);
later there is the statistic (F) calculated in the regression; followed by
stevedores of the model in the intercept and that of the variable.
The last two columns are associated with
the probability of rejecting the coefficient of the intercept, the coefficient
of the variable and the model. In this case, since there is only one
independent variable, the P value of the model and the variable are the same.
In Table 6, it is observed that the
correlation coefficients for the experimental data are not higher than 0.74,
therefore, the adjusted r squared coefficients are not greater than 0.47.
However, in all cases the maximum permissible error level in the model is
0.051, that is, 5.1%.
For the theoretical data models, Table 7,
there are correlation coefficients between 0.92 and 1.00. Which implies
coefficients of determination between 0.83 and 1.00; all the F values are
greater than 40 and the significance of the intercept, models and variable in
all cases have an error level lower than 0.001, that means, they are lower than
one error in each 1000.
Therefore, it can be identified that the
models provide information, through the respective coefficients of the daily
energy average captured in kilowatts per hour for each surface in each of the
cosine and sine components, thus with the previous coefficients it is possible
have the information required to propose the optimization model.
Table 6.
Summary of models associated with experimental
data.
|
Area, experimental data
|
r
|
r^2 adjusted
|
F
|
Intercept
|
Coefficients
|
Intercept of P value
|
Model and variable of P value
|
|
Surface cosine I
|
0,67
|
0,37
|
5,67
|
4,643
|
-0,0021
|
0,000
|
0,049
|
|
Surface cosine II
|
0,67
|
0,37
|
5,76
|
3,798
|
0,0012
|
0,000
|
0,047
|
|
Surface cosine III
|
0,72
|
0,44
|
7,37
|
4,981
|
-0,0030
|
0,000
|
0,030
|
|
Surface cosine
IV
|
0,68
|
0,39
|
6,18
|
3,823
|
0,0011
|
0,000
|
0,042
|
|
Surface sine I
|
0,67
|
0,37
|
5,70
|
3,743
|
0,0016
|
0,000
|
0,048
|
|
Surface sine II
|
0,66
|
0,36
|
5,52
|
4,748
|
-0,0018
|
0,000
|
0,051
|
|
Surface sine III
|
0,73
|
0,47
|
8,03
|
3,784
|
-0,0018
|
0,000
|
0,025
|
|
Surface sine IV
|
0,67
|
0,37
|
5,67
|
4,743
|
0,0018
|
0,000
|
0,049
|
Source: Authors.
Table 7.
Summary of models associated with the theoretical data.
|
Area and theoretical data
|
r
|
r^2 adjusted
|
F
|
Intercept
|
Coefficients
|
intercept of P value
|
Model and variable of P value
|
|
Surface
cosine I
|
1,00
|
0,99
|
1.410,19
|
3,384
|
0,0013
|
0,000
|
0,000
|
|
Surface
cosine II
|
0,93
|
0,85
|
45,14
|
3,876
|
-0,0007
|
0,000
|
0,000
|
|
Surface
cosine III
|
0,99
|
0,98
|
314,72
|
3,222
|
0,0016
|
0,000
|
0,000
|
|
Surface
cosine IV
|
0,93
|
0,84
|
42,08
|
3,859
|
-0,0006
|
0,000
|
0,000
|
|
Surface sine
I
|
0,92
|
0,83
|
40,18
|
3,906
|
-0,0009
|
0,000
|
0,000
|
|
Surface sine
II
|
1,00
|
1,00
|
7.669,80
|
3,318
|
0,0011
|
0,000
|
0,000
|
|
Surface sine
III
|
0,98
|
0,95
|
147,26
|
3,878
|
0,0010
|
0,000
|
0,000
|
|
Surface sine
IV
|
1,00
|
1,00
|
2.446,81
|
3,324
|
-0,0010
|
0,000
|
0,000
|
Source:
Authors.
Construction of the
model
With the calculated coefficients we
already have the information required to propose a linear statistical model for
the case study, in order to evaluate the best combination of the parameters
that make up the MCS, to find the increment of incident radiation on the
surface flat
For its construction was used:
a) Structural design. Figure 5
b) Theoretical and experimental data
base.
c) Objective function
d) Regression coefficients
e) Set of assumptions and restrictions.
The following model is formulated. Which
is carried to a linear program of the VCS.
Figure 5. Variable
system. Source:
Authors.
Objective function
|

|
(2)
|
Results
Mathematical models
proposed
Reference model:
|
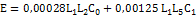

|
(3)
|
Table 8.
Theoretical captured radiation vs theoretical model
|
Inclination angle (β)
|
Theoretical radiation
H(β) (kWh/m2)
|
Radiation with theoretical model H(β)
(kWh/m2)
|
|
0
|
3,82
|
3,904
|
|
15
|
3,81
|
4,975
|
|
30
|
3,76
|
4,518
|
|
45
|
3,68
|
3,998
|
|
60
|
3,57
|
3,451
|
Source: Authors.
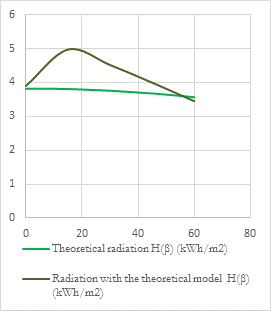
Figure 6. Theoretical captured radiation vs theorical
model. Source: Authors.
In Table 8 and Figure
6, the behavior of the reference model vs the theoretical radiation is shown, a
very similar uptake between the different angles of inclination of the reflective
surfaces can be observed, which indicates it is not relevant, so that the VCS
theoretically would not work.
Experimental model:
|

|
(4)
|
Table 9.
Radiation captured experimental vs
experimental model.
|
Inclination angle (β)
|
Experimental
radiation H(β)
(kWh/m2)
|
Experimental radiation
with experimental model
H(β) (kWh/m2)
|
|
0
|
3,88
|
3,778
|
|
15
|
3,87
|
1,952
|
|
30
|
4,27
|
2,764
|
|
45
|
3,94
|
3,679
|
|
60
|
4,39
|
4,634
|
Source: Authors.

Figure 7. experimental captured radiation vs
experimental model Source: Authors.
In Table 9 and Figure 7, the behavior of
the experimental model vs experimental radiation is shown,
an increase in the uptake can be observed when the VCS presents a 60 ° inclination, which indicates that it is
possible to adapt a flat panel to an VCS to increase solar gain.
Conclusions
The
experimentally measured data show that the flat surface without VCS has a solar
radiation catchment of 3.88 kWh / m2, when coupling the VCS at an angle of 60 °
with respect to the flat surface, it increases to 4.39 kWh /
m2, equivalent to an additional 11.5% of catchment.
When
checking the experimental model, it is observed that the flat surface without VCS
has a solar radiation catchment of 3.77 kWh / m2, when coupling the VCS at an
angle of 60 ° with respect to the flat
surface, it increases to 4.63 kWh / m2, equivalent to an additional 18.5% of
catchment.
Based
on the above, it is shown that it is possible to increase the solar uptake by
means of the reflection provided by the V-concentration system and to improve
the use of incident solar radiation on the flat surface in Bogotá.
The
results show that the solar uptake depends on the inclination angle of the
system, the reflection areas involved in the flat surface, the angle of solar
incidence and the climatic conditions of the site.
The
mathematical model developed based on the experimental and theoretical study
indicates that the V-concentration system can be adjusted to the physical
conditions of a flat solar panel.
References
Chong
K.K. et al. (2012). Study of a solar water heater using stationary V-trough
collector. Renewable Energy 39 (2012) 207-215.
Duffie, J. A., y Beckman, W. A. Solar
Engineering of Thermal Processes. New York: John Wiley & Sons, 919p, 1991.
Hongfei
Zheng et al. (2012) Experimental test of a novel multi-surface trough solar
concentrator for air heating. Energy Conversion and Management 63 (2012)
123–129.
Nova,
N., Pinzón, W., & Quinero, R. (2013). Hacia un nuevo
modelo de cibernética, una aproximación al tercer orden. Bogota:
Universidad Distrital.
Runsheng
Tang y Xinyue Liu. (2011). Optical performance and design optimization of
V-trough concentrators for photovoltaic applications. Solar Energy 85 (2011)
2154–2166.
Saffa Riffat y Abdulkarim Mayere. (2013).
Performance evaluation of v-trough solar concentrator for water desalination
applications. Applied Thermal Engineering 50 (2013) 234-244.
Sangani C.S. y Solanki C.S. (2007)
Experimental evaluation of V-trough (2 suns) PV concentrator system using
commercial PV modules. Solar Energy Materials& Solar Cells 91 (2007)
453–459.
Solanki C.S. et, al (2008). Enhanced heat
dissipation of V-trough PV modules for better performance. Solar Energy
Materials & Solar Cells 92 (2008) 1634–1638.
Spencer, J. W. Fourier Series
Representation of the Position of the Sun. Search 2(5), 172p, 1971.
Tina
G. M. y Scandura
P.F. (2012). Case study of a grid connected with a battery photovoltaic system:
V-trough concentration vs. single-axis tracking. Energy Conversion
and Management xxx (2012) xxx–xxx.