Fecha de Recibido: Enero 24 del 2018
Fecha de Aceptación: Marzo 13 de 2018
Fecha de Publicación: Abril 01 de 2018
DOI: http://dx.doi.org/10.22335/rlct.v10i2.511
* Artículo resultado de investigación “Etapa Superestructural de la Integral”, iniciada en el grupo de Historia de las Matemáticas de la Universidad del Valle y continuada en la Universidad Autónoma de Guerrero, apoyada por CONACYT y por el grupo EDUMATH de la Universidad de Antioquia.
**Magíster en Matemáticas, Docente Tiempo Completo Ocasional, Departamento de Matemáticas, Filiación: Universidad de Pamplona. Correo electrónico: daniel.moran@unipamplona.edu.co Orcid ID: https://orcid.org/0000-0003-1791-2818
*** Doctor en Matemáticas, Profesor Titular del Instituto de Matemática, Facultad de Ciencias Exactas y Naturales, Filiación: Universidad de Antioquia. Correo electrónico: carlos.jaramillo1@udea.edu.co Orcid ID: https://orcid.org/0000-0002-3937-5032
**** Doctor en Ingeniería Matemática, Profesor investigador Titular C de la Facultad de Matemática, Filiación: Universidad Autónoma de Guerrero. Correo electrónico: jsmathguerrero@gmail.com Orcid ID: https://orcid.org/0000-0003-4352-5109
Resumen
El objetivo del artículo es demostrar la transición en la cual el problema “encontrar la cuadratura de una figura plana”, fue posible formalizarla mediante el concepto de integral matemática. Para comprender esta formalización, se abordó un análisis histórico de la evolución del concepto de integral. Conclusión: se propuso una nueva fase en la constitución misma de este concepto, denominada etapa superestructural de la integral.
Palabras clave: Cuadraturas, Epistemología, historia de las matemáticas, integral.
Abstract
The objective of this paper is to show the transition period in which the problem of finding the squaring of a flat figure was possible to formalize it through the concept of mathematical integral. To understand this formalization, a historical analysis of the evolution of the concept of integral will be discussed, and a new phase will be proposed in the constitution of the concept of integral, called the superstructural stage of the integral.
Keywords: quadratures, epistemology, history of mathematics, integral.
Resumo
O objetivo deste artigo é mostrar a transição em que o problema de encontrar o quadrado de uma figura plana foi possível formalizá-lo através do conceito de integral matemática. Para entender esta formalização, será abordada uma análise histórica da evolução do conceito da integral, e uma nova fase será proposta na própria constituição deste conceito, denominado estágio superestrutural da integral.
Palavras-chave: quadraturas, epistemologia, história da matemática, integral.
Introducción
Muchos investigadores han conducido estudios sobre el establecimiento del concepto moderno de integral matemática. Por ejemplo, en artículos como (Lesh & Landau, 1983), (Sfard, 1991) y (Skemp, 1971) muestran la íntima relación entre objeto y proceso, y cómo esto puede ser aplicado a la comprensión de las nociones matemáticas (Caraballo, Rico y Lupiáñez, 2013).. Estudios más especializados sobre la evolución del concepto de integral pueden encontrarse en (Hawkins, 1970), (Michel, 1992) y (Pier, 1996). Además, la afirmación hecha arriba por Piaget sugiere que para entender la manera en la cual las nociones matemáticas emergen como conceptos, es necesario entender cómo ellas dejan de ser simples herramientas para resolver problemas y adquieren un estatus ontológico distinto que amerita un estudio propio e independiente.
En este sentido, este artículo analiza principalmente tres aspectos relevantes e inherentes a la naturaleza del concepto:
· Estudio histórico-epistemológico de la integral.
· Una posible clasificación (desde un punto de vista epistemológico) del concepto.
· Propuesta de una nueva etapa para comprender el concepto.
Estudio histórico-epistemológico de la integral
Analizar la epistemología en el contexto mismo de la historia de las matemáticas, implica necesariamente hablar de los antiguos griegos, quienes fueron capaces de plantear tres problemas que posteriormente se han mostrado que no poseían solución (las técnicas modernas del Álgebra de Galois han demostrado esta imposibilidad). Estos problemas básicamente estaban relacionados con el uso de una regla no graduada y compás, los cuales son:
1.
Sea
un cubo de volumen 
. Encontrar un cubo 
con el doble del volumen, esto es 
.
2.
Sea
un ángulo. Encontrar su tercera parte,
esto es 
.
3.
Sea
un círculo. Encontrar un cuadrado
equivalente (en área) a .
Se puede observar que
estos problemas están íntimamente ligados a la construcción de ciertos números
que no son posibles mediante regla y compás (números trascendentes). Por
ejemplo, el tercer problema es equivalente a la construcción del número
irracional 
, el cual no es
construible con regla y compás. Muchos matemáticos estuvieron interesados en
resolver estos problemas planteados en el siglo V a.C., pero no lograron
resolverlos. Sin embargo, a pesar de estos intentos fallidos, las respuestas
dadas sirvieron como arsenal fértil para el desarrollo de muchas ramas de las
matemáticas. Esas respuestas parciales marcaron, en muchos aspectos, el
derrotero de la evolución matemática por más de 25 siglos (Recalde,
2007, pág. 108). Particularmente nos enfocaremos en el último problema
(conocido como la cuadratura del círculo).
Respuesta de los antiguos griegos
Euclides no logró encontrar el cuadrado equivalente al círculo. Sin embargo, mediante su idea de aplicaciones de áreas logró encontrar el área de un cuadrado equivalente al de una figura rectilínea.
Teorema 1.
(Proposición II,14. Elementos de Euclides). Sea
una figura
rectilínea. Encontrar un cuadrado equivalente a .
Demostración. La idea básica de la prueba de Euclides es la siguiente:
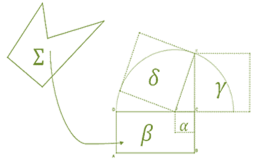
Figura 1: Proposición II,14. Elementos de Euclides. Fuente: Autores
En su libro I,
Euclides muestra cómo encontrar un rectángulo equivalente a una figura
rectilínea. Sea 
un rectángulo
equivalente a 
. Sea 
el
cuadrado sobre la media proporcional entre los segmentos 
y
(el mismo que
determina a ). Afirmamos que 
. En efecto, por la
proposición II,7; Euclides muestra que 
(donde 
es
el cuadrado construido sobre los puntos donde se ha seccionado al segmento ),
y por el teorema de Pitágoras 
. Entonces 
; y por tanto, 
.
La respuesta de Euclides puede considerarse plausible, porque si tenemos un polígono de 4 lados (cuadrado), y duplicamos sus lados (octógono, 8 lados), y así sucesivamente; este polígono tiende a ser un círculo. En términos modernos, decimos esto:
(1)
donde 
es un polígono de 
lados.
No contar con una operación que formalizara los procesos infinitos fue el problema fundamental por el cual los antiguos griegos no lograron dilucidar la noción de límite, que se precisaba para la solución al problema de la cuadratura del círculo. Euclides intuyó la solución y además aportó los elementos primarios para que posteriormente, esta operación del límite tuviera un lugar importante en las matemáticas.
Teorema 2. (Proposición X,1. Elementos de Euclides.) Dadas dos magnitudes desiguales, si de la mayor se quita una magnitud mayor que su mitad, y de la que queda, una magnitud mayor que su mitad, y así sucesivamente, al final quedará una magnitud que será menos que cualquiera de las magnitudes dadas.
Esta proposición está estrechamente relacionada con la urgente necesidad de desentrañar los respectivos procesos infinitos involucrados. En términos modernos, nosotros hablamos de épsilon y deltas, como en la moderna definición del límite matemático, y por supuesto, de la integral. Desde ese punto de vista, Euclides se refiere a lo siguiente:
Sea 
una magnitud y 
. Entonces,
(2)
Aristóteles llamó a
esta proposición el “Axioma de Arquímedes”, puesto que, en éste, Arquímedes se
basó para inaugurar el método exhaustivo. Este es un importante lema para
probar que los círculos son entre sí, como los cuadrados de sus diámetros. A
partir de este hecho, Euclides muestra (en términos modernos) lo siguiente: Sea
una figura plana
acotada por una curva cerrada simple. Sea 
una sucesión de
polígonos inscritos en , estrictamente
creciente. Definimos la siguiente sucesión de diferencias como sigue:
la cual es estrictamente decreciente. Entonces, si es cierto que
(3)
Entonces
(4)
Por condiciones como estas, implícitas en la antigüedad, es que muchos estudiosos de la historia de las matemáticas, sugieren que en la cultura matemática griega existían elementos primitivos de nociones del límite y de la integral, entre muchas otras nociones matemáticas.
Una de las cuadraturas
más importantes resueltas en la antigüedad fue la cuadratura de la espiral de
Arquímedes. En esta, Arquímedes hace uso de la doble contradicción para
demostrar que el área encerrada por la espiral inscrita en un círculo 
es
. Considérese la
siguiente figura:
Sea una espiral de
Arquímedes y sea el círculo que la
circunscribe. Divídase el círculo en partes iguales y sean
las intersecciones de
los sectores del círculo con la espiral.
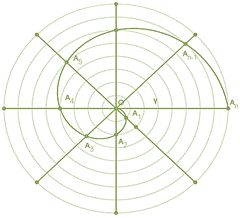
Figura 2. Espiral de Arquímedes. Fuente: Adaptado Autores
Considérese 
, 
, 
, 
. De esta manera, la
región espiral 
contiene una región 
,
formada por sectores circulares inscritos 
,
de radios 
y está contenida en
una región , formada por sectores
circunscritos 
, de radios 
, con lo que se
verifica fácilmente que 
.
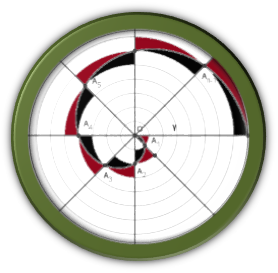
Figura 3. Sectores inscritos (negro) y circunscritos (rojos) de la espiral de Arquímedes. Fuente: Adaptado Autores
La expresión 
es igual al área de
un sector circular y por tanto puede hacerse tan pequeña como se quiera toma lo
suficientemente grande. A continuación se demostrará con el rigor de la doble
reducción al absurdo que el área de la espiral es 
.
Al suponer que 
y sea suficientemente
grande para que se verifique que
(5)
Como 
, entonces se tiene
que 
. Con el fin de llegar
a una contradicción mostraremos que 
. En efecto, Euclides
mostró que los círculos son entre sí como los cuadrados de sus radios, entonces
(6)
donde 
son los sectores del
círculo circunscrito a la
espiral.
De esta última igualdad, al aplicar las propiedades de la suma de proporciones, se obtiene que
(7)
De esta última desigualdad se obtiene que
(8)
lo que contradice la
desigualdad anterior, y de esta manera no puede suceder que 
.
Análogamente tampoco
puede ser mayor, es decir, si 
, se logra llegar a
las desigualdades 
y 
, es decir, a una
contradicción. Luego, por tricotomía, se llega al resultado[2] (Edwards, 1982):
(9)
Al generalizar de
sumas de enteros sucesivos, es posible encontrar la cuadratura de una espiral
generalizada, esto es, espirales de la forma 
, donde tras un
cambio, aparecían ideas de cálculo de parábolas generalizadas 
, obteniendo así
resultados equivalentes a la cuadratura básica:
(10)
La cuadratura básica (que posteriormente se corresponde con la integral de una potencia) se constituye como una piedra angular para el posterior desarrollo de la noción de integral, idea que posteriormente fue retomada por Bonaventura Cavalieri a principios del siglo XVII. Estas generalidades son posible obtenerlas con un procedimiento análogo, de la expresión usada por Arquímedes, de esta manera:
(11)
que finalmente terminan siendo los límites modernos de Sumas de Riemann de una forma generalizada. Lo importante de todo esto es que desde la antigüedad figuraban huellas de la integral, y esto apoya la idea de que el conocimiento matemático más que ser resultados aislados, a través del tiempo, se ha mostrado como una construcción histórica.
La integral en la emergencia del Cálculo: Técnicas de causalidad
El método exhaustivo de Arquímedes (y Euclides) es la base de la definición moderna de integral, porque se evidencia claramente que este método tiene como fundamento el contexto geométrico que contiene las nociones básicas para una comprensión coherente del concepto del límite ligado estrechamente a la definición rigurosa de la integral. Es importante resaltar que en estos tiempos antiguos había un interés por el estudio de las curvas y era posible develar en sus escritos una aproximación al concepto de límite. Además, había necesidad de que en el desarrollo del tiempo surgieran otras construcciones entre las cuales está una noción de función, para que ligada al concepto de límite, pudiera consolidarse el concepto de integral. Es por esto que un análisis a la evolución del estudio de las curvas, nos permite determinar cómo a través del tiempo, el razonamiento matemático y el establecimiento de una formalización pertinente, alcanza estos logros para el desarrollo del cálculo.
La integral en la emergencia del Cálculo: Técnicas de causalidad
El cambio drástico en
el tratamiento de curvas fue dado por Descartes (1596-1650) en su importante
trabajo Discurso del método, se puede apreciar que él cambió la forma de
hacer matemáticas, estableciendo una conexión entre los elementos del cálculo
aritmético y los de segmento y plano la geometría. A través de un sistema de
dos rectas que no se superponen (posiblemente ortogonales), él introdujo lo que
hoy día es llamado plano cartesiano. Dada una curva ,
es posible asignar una ecuación que la gobierna, de la forma 
. Descartes también
define cómo es posible establecer una aritmética entre segmentos; por ejemplo,
multiplicación y extracción de raíces. En este sentido, establece una relación
biunívoca entre curvas y ecuaciones: a una curva le corresponde una única
ecuación cartesiana, salvo múltiplos de la misma. Así, la parábola deja de
estar amarrada a la existencia de un cono, y pasa a existir ella misma mediante
el plano cartesiano, como el conjunto de puntos 
tales que 
.
Los indivisibles de Cavalieri
El rigor de Arquímedes era demasiado tedioso para demostrar que una figura correspondía a la cuadratura de otra. El método consistía en una doble reducción al absurdo: asumían que era mayor, o que era menor; y en ambos casos, se llegaba a una contradicción. Con el fin de evitar esta tediosa manera geométrica de demostrar resultados, los matemáticos del siglo XVII usaron algunos métodos heurísticos, métodos poco rigurosos, pero que generaron prolíficos resultados. Por ejemplo, Bonaventura Cavalieri (1598-1647) establece una técnica conocida como la de los “indivisibles” que grosso modo, consiste en lo siguiente:
Figura 4. Indivisibles de Cavalieri para regiones. Fuente: Adaptado Autores
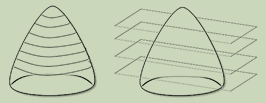
Figura 5. Indivisibles de Cavalieri para superficies. Fuente: Adaptado Autores
Un indivisible es un
objeto geométrico de una dimensión inmediatamente menor, por ejemplo, los
indivisibles de una línea, son puntos; los indivisibles de una región, son
líneas; los indivisibles de un volumen (3D) son planos (2D) y así
sucesivamente. En otras palabras, una región puede ser obtenida por “suma de
líneas” de una manera conveniente. Cavalieri llamó “ominus” a este tipo de suma.
“Ominus linae” significa “suma de todas las líneas”. El símbolo que usó fue 
. Él, mediante la
geometría de Descartes, probó que:
(12)
Con métodos
algebraicos. Además, hizo una generalización para grande.
Se observa entonces, que cualquier parecido con la realidad no es pura coincidencia, en tanto que, al utilizar métodos algebraicos, Cavalieri (intuyendo la noción de límite) encontró una generalización para lo que posteriormente fue la integral de una potencia:
(13)
Queda una pregunta abierta: ¿Cómo es posible que la suma de todas las líneas (cuya integral sabemos, es igual a cero) pueda dar como resultado una región plana?
Cuadraturas de Fermat y de Wallis
Con el fin de salvar un poco el rigor perdido con los indivisibles de Cavalieri, Fermat propuso una idea similar de suma, pero añadiendo elementos homogéneos. La idea era simple: añadir rectángulos de base muy pequeña y, por lo tanto, la suma de las áreas de los mismos es igual al resultado del área del conjunto de rectángulos considerados. Cuando la base se acerca a cero (modernamente, esto es considerar una partición del dominio cuya norma tienda a cero) entonces el área inscrita tiende a ser el área a calcular.
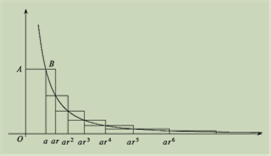
Figura 6. Cuadratura de la hipérbola por Fermat
Fermat realiza este
proceso, a través de progresiones geométricas. En este caso (la hipérbola), sea
y consideremos los
puntos de abscisas 
; entonces los
rectángulos inscritos tienen como área:
(14)
Y los triángulos circunscritos tendrán por área
(15)
Entonces, la
cuadratura (el área bajo la curva) está acotada por las dos expresiones
anteriores. Sea 
la cuadratura,
entonces:
(16)
Como la desigualdad es
válida para todo , él concluye que el
área 
. Vemos cómo en las
consideraciones establecidas por Fermat, se encuentran elementos de la integral
definida, inscribiendo y circunscribiendo rectángulos infinitamente pequeños.
La discusión acerca de los indivisibles vs. infinitesimales (como en Cavalieri)
es un amplio tema de discusión. (Hawkins, 1970) es una excelente referencia
para profundizar en ello.
De otro lado, es importante destacar que Wallis logró establecer una aritmética para los indivisibles. En su obra Arithmetica Infinitorum establece que el área de un rectángulo es el producto de la base por la altura, con el propósito de asignar un número al área de una región plana. Con esta idea, él pretende formalizar el área de figuras planas. Por lo tanto, asumiendo esta postura, al parecer estaba intentado analizar la formalización de la noción de función:
Es decir, asignar un
número a eso que llamamos área. Pero no contamos con esa reglilla que mida,
llamada 
. Los esfuerzos
posteriores buscan formalizar la idea de número real. Para profundizar en la
relación número y magnitud, ver (Dhombres, 1980).
Es importante tener en
cuenta que Euclides ha resuelto el problema de encontrar la cuadratura del
rectángulo; Arquímedes hizo lo mismo para la parábola; Cavalieri hizo una gran
contribución al generalizar la cuadratura de las curvas de la forma 
, donde es
un entero positivo (ya que emula la dimensión);
Roberval encontró la cuadratura de la cicloide y Fermat la de la Hipérbola. Los
procedimientos son diferentes e independientes (no es el mismo proceso de
cuadratura de la parábola que el de la hipérbola, son tratamientos distintos).
Los matemáticos son conscientes de que existe un problema (el problema de las
cuadraturas), pero hay una serie de técnicas independientes para resolver el
problema y casos de curvas muy particulares. La sistematización de todas estas
técnicas es necesaria, la cual permite el tránsito de lo particular a lo
general, y así tener un algoritmo de resolución. Este trabajo de
sistematización fue hecho por dos gigantes: Newton y Leibniz.
Las contribuciones de Newton y Leibniz
La sistematización de
todas estas anteriores técnicas de cuadraturas se deben a Newton y Leibniz.
Newton recogió toda la tradición de cuadraturas y anticuadraturas y logró
generalizar los resultados, los cuales consignó en algunas tablas. Newton
relacionó estos problemas con elementos físicos que dependen del tiempo.
Imaginó una curva como un punto moviéndose en el espacio, y los problemas
relacionados con cuadraturas y anticuadraturas, con la velocidad con la cual
los puntos se mueven. Un punto que describe un movimiento en el espacio, le
llamó fluente, y a la velocidad de la fluente con respecto al tiempo, la
llamó fluxión. En su libro De Methodis, Newton resuelve varios
problemas que son pilares en el desarrollo del cálculo (incluso, en los currículos
modernos!): Dada una fluente (función), encuentra su fluxión (derivada); dada
la fluxión, encontrar la fluente. También habla de cuadraturas de curvas. El
maestro de Newton, Isaac Barrow, fue el primero en reconocer la relación
inversa entre cuadratura y anticuadratura, que fueron las primeras aportaciones
del Teorema Fundamental del Cálculo. Un problema importante de los desarrollos
de Newton, fue la relación de estos resultados matemáticos con la dependencia
del tiempo y el uso conveniente de ciertas cantidades que se podrían anular
(porque tienden a cero), pero podría ser dividido porque ellas eran diferentes
de cero. Esta idea actualmente no tiene problema porque sabemos que la palabra
“tiende” tiene un enfoque explícito, y está amparada bajo el concepto de
límite; pero en su tiempo, Newton no tenía los elementos necesarios que le
permitiera fundamentar estos resultados, los cuales fueron criticados
fuertemente por el Obispo Berkeley[3].
Otro problema era que el uso de la notación de Newton era bastante tediosa: la
derivada la denotaba como 
, la segunda derivada
como 
, la tercera 
, y así sucesivamente.
Leibniz de manera independiente, aportó con la adecuada notación que compila
toda la esencia de lo que es la integral, la cual ha resistido el paso de la
historia: 
.
La emergencia de la integral
En el siglo XIX, hay un cambio significativo –ontológico - del concepto de integral. Los matemáticos se dan cuenta de que la integral no es un problema secundario del cálculo, como tal vez sucedió con Newton y Leibniz.
Bernoulli: el nacimiento de la integral
En una nota histórica de 1692, los Bernoulli (aunque la memoria tiene el nombre de Johann, muchos historiadores señalan el hecho de que Jakob tiene mucho de la paternidad del concepto) resuelven el problema de la isócrona y la catenaria, e introducen la palabra integral por primera vez. La idea de integración aparece como una herramienta para resolver algunas ecuaciones diferenciales, y con esta idea es como los Bernoulli resuelven estos problemas. Tal como es mencionado por Recalde, es un hecho epistemológicamente significativo, ya que “con la incorporación de un nombre para designar una operación específica, se identifica una noción que amerita un tratamiento especial” (Recalde, 2007, pág. 113). Los matemáticos han reconocido que la integral merece un adecuado tratamiento, y no es simplemente un aspecto secundario del Cálculo.
Para Leibniz, la
integral tiene un sentido particularmente geométrico, donde la operación
consiste en la suma de rectángulo infinitamente pequeños 
,
que podrían ser simbolizados como 
. Posteriormente, en (Bernoulli, 1691) se reconoce la integral como la inversa del diferencial:
¿Qué es 
?
Se ha visto antes cómo encontrar diferenciales de cantidades: ahora, al revés, vamos a mostrar cómo encontrar las integrales de los diferenciales, es decir, las cantidades de las que son las diferencias.
Es
decir, 
significaría 
.
(Bernoulli, 1691)
La representación en Series de Fourier
Fourier en su investigación acerca de la conducción del calor en un cuerpo sólido, mostró que este problema responde a la siguiente ecuación diferencial:
(17)
Obteniendo una función trigonométrica como solución de esta ecuación diferencial:
(18)
en donde los coeficientes de Fourier son determinados de la siguiente manera,
(19)
Esto significa que la representación de una función en series de Fourier está sujeta a la existencia de las integrales mencionadas en su intervalo correspondiente. El hecho de que los coeficientes de Fourier sean calculados como integrales definidas implica definir la integral para funciones arbitrarias. La emergencia de funciones de este tipo superó en cierto modo la concepción de función dada por Euler como una expresión analítica. Considerar la integral como antiderivada no tenía mucho sentido cuando se hablaba de funciones discontinuas, motivó a reconsiderar el concepto de integral. Problemas tales como «continuidad», «discontinuidad», «discontigüidad», etc., hicieron pensar que el problema pedía un retorno a la geometría. Fourier identificó la integral como un área, plantearon la necesidad de volver a la interpretación geométrica de la integral.
Esta concepción marca
un hecho importante en la Historia de la Integral, ya que Fourier introdujo una
notación la cual fue adoptada universalmente para las integrales definidas.
Queda la siguiente pregunta en Fourier: ¿Cómo definir 
, como un área, cuando
es arbitraria?
La integral de Cauchy
La comprensión de Cauchy es un punto de llegada en la maduración del Análisis Matemático, tal como lo entendemos hoy en día. En 1821 él escribió un libro trascendental en la historia de las matemáticas llamada Cours d’Analyse de l’École Royale Polytechnique. 1st Partie. Analyze Algebrique. Después de todas las discusiones acerca del problema de la conducción del calor, la cuerda vibrante, etc., se ha mostrado que la definición de función dada por Euler como una expresión analítica tiene ciertas limitaciones. En este sentido, Cauchy aporta una definición de función bajo un concepto que ha sido de gran trascendencia y que durante 25 siglos fue evadido dada la falta de elementos matemáticos para su comprensión. Esta definición significó la formalización de los procesos potencialmente infinitos: el paso al límite. Bajo el concepto de límite, define lo que es cantidad variable, función, continuidad, convergencia, etc. Define la derivada y la integral como un límite particular.
Un aspecto importante en las definiciones de Cauchy es la ausencia de soportes geométricos (ni siquiera con fines aclaratorios), pero todo esto está soportado bajo el concepto de límite y el álgebra de desigualdades: Cuando los valores que toma una variable particular se acercan indefinidamente a un valor fijo, por lo que sólo se diferencian de él tan poco como desee, entonces este último valor, se le llama el límite de todos los anteriores (Cauchy, 1821), que posteriormente utilizó una notación propia de Weierstrass, corresponde de manera moderna a,
(20)
Esta definición desconoce los problemas de los procesos infinitos cuya existencia está asegurada en el álgebra de desigualdades.
En la línea de desarrollo de la integral, es un punto de llegada, donde tenemos el concepto de integral en su forma refinada, como una noción de las matemáticas, basada en el concepto de límite. En términos generales, la integral es la generalización de un límite de sumas infinitamente pequeñas. Por lo tanto, Cauchy da la definición de integral y lo hace para funciones continuas, así:
Definición 1.
(Integral de Cauchy) Sea una función 
,
definida en el intervalo 
. Sea la partición 
, se define la
sucesión de diferencias, 
, y la suma:
El valor de 
depende de 
y
de
(21)
En caso de que el
límite exista cuando tiende
a infinito y cuando 
tiende a cero, entonces
este límite se denomina:
(22)
La integral después de Cauchy
Las obras de Cauchy
constituyen una importante ruptura conceptual, donde los referentes geométricos
son exiliados y sólo se basa en el lenguaje analítico, definiendo la integral
como un concepto puramente del Análisis. Pero a pesar de esto, no ignora su
interpretación geométrica como el área bajo la curva como una aplicación de la
integral definida. Pero la respuesta de Cauchy va más allá, mostró que una
integral puede existir, pero no necesariamente indica cómo se calcula; es
decir, ha demostrado que su forma de definir la integral definida no depende
necesariamente de la existencia de la antiderivada. Ahora, en la perspectiva de
Fourier y Cauchy surge otra pregunta: ¿Se puede definir 
para cualquier
sucesión de ordenadas? El matemático alemán Gustav Dirichlet dio respuesta
negativa a esta pregunta con el siguiente contraejemplo:
(23)
donde la integral no
tendría ningún significado y donde 
no tiene un cierto
valor. Así pues, la integral de Cauchy no es suficiente para abarcar esas funciones
arbitrarias de las cuales habló Fourier. Sin embargo, Dirichlet propuso una
salida a su propio problema. A pesar de que su función característica 
es densamente
discontinua, podría ser que las funciones que eran integrables eran aquellas en
las que sus puntos de discontinuidad podían determinarse de cierta manera.
Es decir, la
definición de Cauchy abarca aquellas funciones continuas y discontinuas, pero
con un número finito de discontinuidades. Dirichlet dice que no sólo serían
aquellas funciones que tienen discontinuidades finitas, sino que podrían ser
infinitas, siempre y cuando formaran un conjunto diseminado (denso en ninguna
parte), y así exista. Esta
afirmación se conoce como la condición de Dirichlet.
La integral de Riemann
La preocupación de Dirichlet por la integración de funciones discontinuas fue retomada por su brillante discípulo Bernhard Riemann en su Habilitationsschrift en 1854. Riemann extendió la definición de integral de Cauchy reconociendo que la condición de continuidad no era esencial.
Definición 2.
(Integral de Riemann). Una función definida
y acotada en un intervalo 
es integrable si la
suma
(24)
va tendiendo a un
único valor límite cuando los 
tienden a cero, donde
y 
. Ese valor límite va
a ser, por definición, .
Expuso dos condiciones necesarias y suficientes sobre integrabilidad que son equivalentes:
(R1) La función es
integrable en el intervalo 
si y sólo si 
, 
, 
, tal que para toda
partición , con 
, se tiene que 
, donde 
, con 
.
(R2) es
integrable en un intervalo si y sólo si, para
toda partición , se tiene que, 
, donde 
.
Con esto, Riemann pudo demostrar que la condición de Dirichlet no era necesaria, porque podía ser mucho más discontinua que lo que su maestro había imaginado. Riemann en su tesis doctoral de 1854 mostró ejemplos con los que demostró que su definición de integral acogía un conjunto de funciones más amplias que las de Cauchy. Pero, aun así, con la definición de integral dada por Riemann, no es posible integrar la función de Dirichlet. Por otra parte, el matemático italiano Ulise Dini demostró que la integral de Riemann tenía defectos, puesto que no se preserva bajo el paso al límite. Los detalles de esta demostración se pueden ver en (Grattan-Guiness, 1982, pág. 159).
La integral de Lebesgue
En busca de otra dirección, a finales del siglo XIX, la teoría de la integración de Riemann se orientaba hacia el estudio de los conjuntos y sus medidas. A finales del siglo XIX, hubo una gran confusión topológica con respecto a la medida de los conjuntos. Hubo resultados que no eran del todo correctos, como las condiciones de Hankel y Lipschitz para la medida de conjuntos. Esta confusión topológica era comprensible: la teoría de conjuntos surgió de manera seria e independiente. El punto de culminación fue la teoría de integración de Lebesgue, donde tomó algunos elementos conceptuales de Jordan y Borel en la formulación de la teoría de la medida.
Con todos estos insumos obtenidos hasta ahora, y a través de 25 siglos de desarrollo matemático, se ha querido formalizar el problema de las cuadraturas. Además, Lebesgue en su tesis doctoral, desarrolla la teoría de la medida y reconoce que para resolver los problemas que el formalismo analítico se ha visto limitado, debe volver al problema principal y milenario de las cuadraturas: un aspecto geométrico. Reconoce que las bases conceptuales de la teoría de la medida se basan en tres características fundamentales:
i. Existencia de un conjunto cuya medida sea diferente de cero.
ii. La medida es invariante bajo traslaciones
iii. La medida de una unión finita o numerable de conjuntos, disjuntos dos a dos, es igual a la suma de las medidas de los conjuntos.
Lebesgue comprende que para resolver los problemas actuales de la medida debe retornar a las bases conceptuales que están en las raíces de los conceptos matemáticos desde sus inicios. En su tesis doctoral reconoce que debe volver a leer a Euclides y Arquímedes, y así darse cuenta de que la respuesta se encontraba allí, cambió el concepto de medida relativa al de medida absoluta, en consecuencia, Lebesgue define la integral como sigue:
Definición 3.
(Integral de Lebesgue). Sea una
función definida en el intervalo , tal que:
1. Existen
y ,
tales que 
, para todo 
2. Para
todo 
entre y
, el conjunto 
es medible
Se
toma una partición de 
,
y se definen los
conjuntos 
, para 
y
, para 
,
los cuales son medibles. Sean las sumas,
Entonces es
de carácter Lebesgue-Integrable si cuando tiende
a infinito y 
tiende a cero (es
decir, la norma de la partición tiende a cero: 
) las dos sumas
coinciden; en este caso se escribe,
(26)
Por lo tanto, Lebesgue muestra que, en efecto, es una generalización de la integral de Riemann, ya que toda función R-Integrable es L-Integrable.
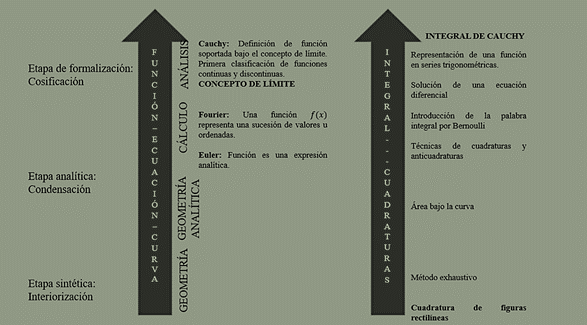
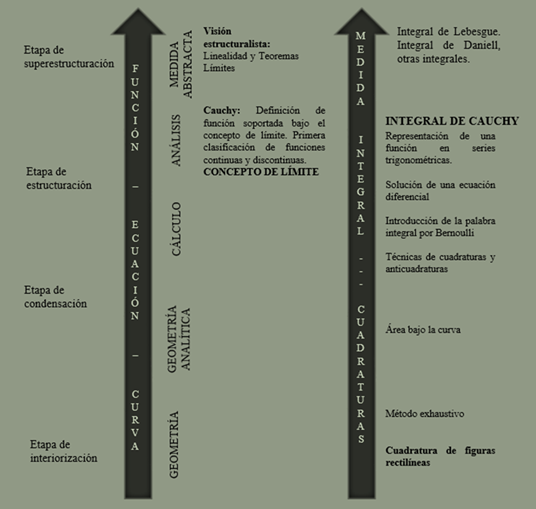
Una posible clasificación desde un punto de vista epistemológico del concepto La evolución de los conceptos matemáticos juega un papel central en la Epistemología, y para los investigadores en educación matemática es importante reconocer el tránsito histórico-epistemológico-ontológico de un concepto matemático. Una visión de este tipo, proporciona herramientas pedagógicas y conceptuales tanto para los educadores matemáticos como para los mismos matemáticos; con el propósito de lograr una mayor comprensión de los diferentes conceptos que subyacen a las estructuras matemáticas hasta el momento emergidas en el transcurso de la construcción de esta disciplina desde sus inicios.
En el marco teórico propuesto en (Sfard, 1991) se resaltan las etapas a través de las cuales un concepto pasa de su versión de herramienta a su versión de noción formal: interiorización, condensación y cosificación, es así como se puede apreciar en esta teoría un esfuerzo por aclarar cada una estas categorías epistemológicas que tratan de explicar, a través de la historia, los distintos enfoques con los que ha venido construyendo y al ampliar la construcción del conocimiento matemático.
La idea de Sfard va de la mano con la idea que promulga Piaget, donde se reconoce que los conceptos nacen de las acciones y necesidades que todos los seres humanos tenemos (Piaget, 1970). Las personas primero necesitaron contar y medir; para contar, utilizaron representaciones numéricas; para medir, comparaban; por lo tanto, el problema de las cuadraturas desató una gran cantidad de ideas hasta llegar a su generalidad: la integral matemática. La figura 7 pretende mostrar ese desarrollo de la integral que estuvo latente al desarrollo del concepto de función, donde se parcela en los tres estadios propuestos en (Sfard, 1991)
