Fecha de Recibido: Febrero 2 del 2018
Fecha de Aceptación: Marzo 14 de 2018
Fecha de Publicación: Abril 01 de 2018
DOI: http://dx.doi.org/10.22335/rlct.v10i2.571
*Artículo resultado de objetivo de investigación del proyecto “Comprensión onto-histórica de la matemática en la trayectoria de la educación a distancia en la universidad Francisco de Paula Santander “investigación aprobada por el Fondo de investigaciones universitarias FINU-UFPS
** Magister en Ciencias. Ingeniero electrónico, Candidato a Doctor en Matemática Educativa en la especialidad de Matemática Educativa. Filiación: Centro de Investigación y de Estudios Avanzados del I.P.N. CINVESTAV-México. Correo electrónico: freddymatedu@gmail.com fvillamizar@cinvestav.mx. Orcid ID: https://orcid.org/0000-0003-0628-2064
*** Magister en Educación Matemática Licenciada en Matemáticas y Física. Especialista en Estadística Aplicada.. Filiación: Universidad Francisco de Paula Santander. Correo electrónico: olgarincon@ufps.edu.co . Orcid ID: https://orcid.org/0000-0002-8080-496X
**** Postdoctora en Imaginarios y representaciones sociales, Doctora en Educación. Magister en Gerencia Educativa. Licenciada en Matemáticas y Física. Especialista en Estadística Aplicada. Filiación: Universidad Francisco de Paula Santander. Correo electrónico: mawency@ufps.edu.co . Orcid ID: https://Orcid.org/0000-0001-8285-2968
Resumen
El presente artículo tiene el objetivo de analizar la influencia del uso de tecnología la digital, acompañada de una didáctica para la concepción y solución de problemas aplicados, en un enfoque de enseñanza activa, en temas de optimización. La metodología siguió un enfoque cualitativo, a partir de un taller con profesores, en el cual se resolvieron problemas en el contexto de máximos y mínimos de forma analítica y dinámica mediante el software Geogebra. Resultados señalan la necesidad de implementar secuencias didácticas que guíen a la concepción de la optimización, la herramienta motiva la fase de enseñanza al permitir la simulación y modificación de heurísticas en los estudiantes al solucionar un problema. Conclusión: la tecnología digital es factor motivante en la enseñanza, que permite la visualización de representaciones de objetos matemáticos de manera dinámica, ayuda a la conceptualización si y solo si se apoya de secuencias didácticas.
Palabras clave: escenarios virtuales, geometría dinámica, problemas de optimización, registros de representación.
Abstract
The present paper has the objective of analyzing the influence of the use of digital technology, accompanied by a didactic for the conception and solution of applied problems, in an active teaching approach, in optimization topics. The methodology followed a qualitative approach, starting from a workshop with professors, in which problems were solved in the context of maximums and minimums in an analytical and dynamic way using Geogebra software. Results point out the need to implement didactic sequences that guide the conception of optimization, the tool motivates the teaching phase by allowing the simulation and modification of the heuristics in students when solving a problem. Conclusion: digital technology is a motivating factor in teaching, which allows the visualization of representations of mathematical objects in a dynamic way, helps the conceptualization if and only if it is supported by didactic sequences.
Keywords: virtual scenarios, dynamic geometry, optimization problems, representation registers.
Resumo
A presente pesquisa tem como objetivo analisar a influência do uso da tecnologia digital, acompanhada de uma didática para a concepção e solução de problemas aplicados, em uma abordagem de ensino ativo, em tópicos de otimização. A metodologia seguiu uma abordagem qualitativa, a partir de um workshop com professores, em que os problemas foram resolvidos no contexto de máximo e mínimo de forma analítica e dinâmica usando o software Geogebra. Os resultados apontaram a necessidade de implementar sequências didáticas que orientam a concepção de otimização, a ferramenta motiva a fase de ensino ao permitir a simulação e modificação de heurísticas em estudantes ao resolver um problema. Conclusão: a tecnologia digital é um fator motivador no ensino, que permite a visualização de representações de objetos matemáticos de forma dinâmica, ajuda a conceituar se e somente se for suportada por sequências didáticas.
Palavras-chave: cenários virtuais, geometria dinâmica, problemas de otimização, registros de representação.
Introducción
Una de las formas de la práctica docente se identifica con la enseñanza tradicional, siendo ésta de carácter pasivo por parte del estudiante, quien es espectador de lo que el profesor trasmite y plasma sobre un tablero, lo cual, conlleva al aprendizaje memorístico y la dificultad en la adquisición de los conceptos (Cuevas y Pluvinage, 2003). Esto permite cuestionarse acerca de, ¿cómo promover una mejor comprensión conceptual en matemática aplicada, para hacer partícipe al estudiante en la construcción del conocimiento?
Al respecto, investigaciones evidencian que las tecnologías digitales ofrecen gran cantidad de recursos, los cuales, al ser acompañados de una didáctica adecuada, pueden promover una forma activa de construir los conceptos matemáticos (Vergel, Rincón, y Zafra, 2017; Cuevas, Villamizar y Martínez, 2017). Actualmente, la tecnología crece a pasos agigantados, considerada por ello, una variable social que debe enfrentar quien enseña, sobre todo ante una generación de personas que son consideradas nativas del mundo de las tecnologías digitales, es decir, aquel ser humano mencionado por Serres (2014) llamado la pulgarcita, por su capacidad de manejar los pulgares para enviar información, y que por lo general, su aprendizaje está mediado por un artefacto tecnológico digital.
El National Council of Teachers of Mathematics NCTM (2000), menciona que el uso de las tecnologías digitales debe incluirse en las propuestas curriculares, argumentando que las calculadoras y computadoras son herramientas esenciales para la enseñanza, aprendizaje, y desarrollo de la matemática en finanzas y otras áreas y disciplinas, facilitan la producción de imágenes visuales de las ideas matemáticas, la organización y el análisis de datos entre otras más ventajas. En complemento, Cuevas, Villamizar y Martínez (2017) argumentan que las tecnologías digitales deben ser un recurso incluido en las actividades académicas, como herramienta de apoyo que permitan al estudiante enfocarse realmente en los conceptos, razonamientos y resolución de problemas, siempre y cuando vayan acompañadas de un marco didáctico.
Investigaciones proponen actividades didácticas con uso de la tecnología mediante la aplicación de Escenarios Didácticos Virtuales Interactivos o EDVI (Cuevas, Rodríguez y González, 2014; Cuevas y Villamizar, 2015). En el artículo se analizó uno de los problemas de optimización implementados, para introducir al estudiante en la resolución de problemas desde una perspectiva dinámica mediante el diseño y uso de un Escenario Virtual (EV). Éste, se construyó en Geogebra (Hohenwarter, 2018) y aunque no se explicitó un cuestionario didáctico, el diseño del EV incluyó elementos de la didáctica manifestada por Cuevas y Pluvinage (2003), la cual plantea que, en lo posible se debe partir de un contexto o situación problema para introducir determinado concepto matemático.
En este sentido, la didáctica Cuevas y Pluvinage (2003) permite el uso de diversos registros de representación semiótica (Duval, 1998), visualizados con ayuda del EV, por ejemplo, la gráfica de una función que representa el volumen de una caja en función del corte realizado a una lámina rectangular (Figura 1).
Respecto al problema de introducir en el campo de la optimización, investigaciones previas (Cuevas y Moreno, 2004; Vergel, Rincón y Zafra, 2017) han reportado que los estudiantes tienden a solucionar algorítmicamente los problemas relacionados con los criterios de máximos y mínimos, lo cual, conlleva a resultados sin sentido, debido a una incomprensión en el concepto de función y posibles dificultades en conceptos de precálculo. Al final de la experiencia se consideraron ventajas y desventajas ofrecidas por la herramienta digital para resolver el problema, respecto de su resolución a lápiz y papel en el campo de la optimización.
Metodología
La experiencia didáctica, se propuso apoyada en un taller (de dos sesiones de tres horas) en el que participaron cincuenta profesores de matemáticas de nivel bachillerato y profesional en la modalidad a distancia. Se dispuso de un aula con un dispositivo de proyección, un computador por profesor y el uso del software de geometría dinámica Geogebra en cada equipo.
Inicialmente se planteó a los profesores participantes, un problema de optimización para resolverlo analíticamente con lápiz-papel y luego con el uso de Geogebra. La metodología de investigación propuesta es de tipo cualitativo (Stake, 1999; Bikner, Knipping y Presmeg, 2015); al final se describen los resultados sobre la discusión y la reflexión de los profesores, sobre qué posibles ventajas les brindó el uso de Geogebra como herramienta mediadora en la resolución del problema.
Secuencia didáctica y resolución del problema
La actividad se realizó de forma guiada por el profesor ponente y de forma participativa con cada uno de los profesores participantes. Se da inicio con el planteamiento de una situación problema contextualizada (Vergel, Rincón, Salazar, 2017), en el campo de la optimización. Bajo el punto de vista de los problemas ejemplificados en Granville (2017), se interpreta la optimización como una forma de encontrar el mejor elemento (con respecto a algún criterio) de un conjunto de elementos disponibles; los cuales pueden ser cantidades de algo, tal como se plantea en la situación problema del taller realizado con los profesores, descrita a continuación:
Una caja rectangular se fabrica con una pieza de cartón por 24 pulgadas de largo por 9 de ancho, de la cual se cortan cuadrados idénticos a partir de las cuatro esquinas y se doblan los lados hacia arriba, como se muestra en la Figura 1. Determine las dimensiones de la caja de volumen máximo ¿Cuál es este volumen? (Purcell, Varberg, Rigdon, 2007, p. 167; modificado de Granville, 2017, p. 72).
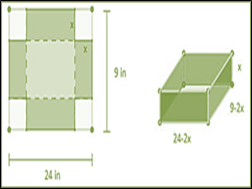
Figura 1: dimensiones de la caja rectangular construida desde Geogebra. Fuente: Autores
El diseño de la situación propuesta obedece a un elemento de la didáctica Cuevas y Pluvinage (2003) para la enseñanza de las matemáticas, la cual plantea partir de un problema en contexto para introducir al estudiante en una futura construcción o exploración de un concepto matemático, que en este caso se refiere al dominio, raíz de una función y los máximos y/o mínimos en un problema de optimización.
Resolución a lápiz y papel: resolución analítica
Una alternativa de solución con lápiz y papel desarrollada por lo profesores fue:
a) A partir de un gráfico como el mostrado en la Figura 1, se asignaron variables: x al ancho del recorte de la pestaña, de este modo el largo de la caja es igual a 24-2x, el ancho 9-2x y alto x.
b) A partir de las dimensiones, se establece que, la expresión del volumen de la caja en función de x es:
![]() (1)
(1)
Al Simplificar (1) se obtiene:
![]() (2)
(2)
La ecuación (2) es una función cúbica que representa el volumen de la caja en función del corte cuadrado realizado a la lámina rectangular. Su representación gráfica se muestra en la Figura 2.
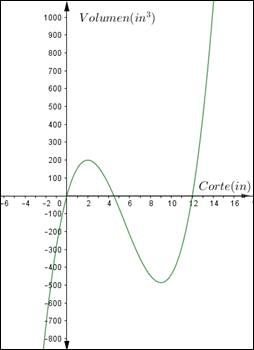
Figura 2: Representación gráfica de V(x) realizada en Geogebra. Volumen vs corte de la caja. Fuente: Autores
El volumen máximo entre x=0 y x=4.5 in (Figura 2) se logra cuando el corte está alrededor de 2 pulgadas. Sin embargo, la forma analítica para calcular el valor óptimo usada por los profesores, fue aplicado el criterio de la primera derivada:
![]() (3)
(3)
Al igualar a cero la expresión (3), se obtiene:
![]() (4)
(4)
Al despejar la x en (4) obtenemos los puntos estacionarios x=9 y x=2, pero como no es posible hacer un corte de 9 pulgadas, entonces se considera que el corte óptimo debe ser de 2 pulgadas. Para dicho corte el volumen máximo es de V (2) = 200 pulgadas cúbicas.
Sin embargo, la expresión algebraica obtenida en (2) es una función cuyo dominio son todos los reales. De modo que, al hallar el volumen de la caja con un recorte de 14 pulgadas, se obtiene V (14) = 1064 pulgadas cúbicas, lo cual es un valor aceptado porque es positivo, pero que no tiene sentido dentro del problema, ya que el recorte de la pestaña cuadrada deber ser mayor que 0 y menor que 4.5 pulgadas. Lo anterior es algo que analíticamente resulta desapercibido para algunos profesores, que, al desarrollar el problema, no tuvieron en cuenta el significado del valor de las raíces de (2), para acotar la función en un dominio específico. El anterior resultado coincide con la hipótesis planteada por Cuevas y Moreno (2004), quienes argumentan que existen dificultades en la comprensión de significados alusivos a función, como el dominio y raíces; generalmente se opta por una resolución donde se siguen esquemas algorítmicos de manera memorística.
Resolución dinámica: Escenario Virtual (EV).
Una vez realizado el problema analíticamente (lápiz y papel) se les planteó a los profesores lo siguiente: ¿qué sucedería si se modifica el valor de los parámetros que determinan el largo y el ancho de la lámina? En respuesta, cambiarían el volumen y el recorte, para que el volumen sea el más óptimo (en este caso máximo), por lo tanto, se debe replantear nuevamente la ecuación que ligue el recorte con los nuevos parámetros.
Para lo anterior, el profesor ponente, debe tomar el papel de guiar la construcción dinámica del problema de la caja, al utilizar el software Geogebra. En dicha construcción se exploran las diversas funciones de la herramienta digital como el trazo de rectas paralelas, perpendiculares, intersección en un punto, y la aplicación de conceptos como el de lugar geométrico, simetría axial y central, mediadas igualmente con el programa.
Como un resultado del taller, se construyó un EV compuesto de dos vistas gráficas. La vista gráfica 1, muestra la imagen de la lámina y su respectiva transformación en una caja sin tapa (Figura 3). Por medio de los deslizadores “base y altura” se cambia de forma dinámica los parámetros que definen la lámina rectangular, de modo que se pueda ajustar a diferentes valores según sea redactado el problema.
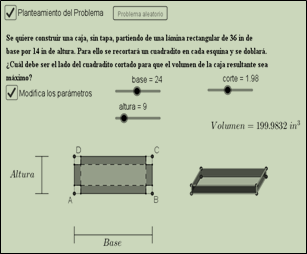
Figura 3. Vista gráfica 1 del EDVI caja dinámica. Fuente: Autores
Al mover el deslizador “corte” se simula una familia de cajas de manera dinámica, de modo que en la vista gráfica 2 (Figura 4), se aprecia el rastro o lugar geométrico que marca el punto con coordenadas (corte, volumen) que representa el volumen de la caja para determinado corte.
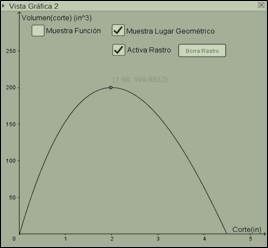
Figura 4. Vista gráfica 2 del EDVI caja dinámica. Fuente: Autores
El EV mostrado en la Figura 3 y 4, usa varios registros de representación y facilitó la visualización de cierta realidad simulada y su relación con las matemáticas, en este caso, la construcción de la caja con la función gráfica que representa su volumen para determinado corte. La función mostrada en la vista gráfica 2 del EDVI (Figura 4), es trazada dentro del dominio aceptado para el corte de la caja. Una de las ideas previas inadecuadas que presentan algunos profesores es pensar que el volumen máximo se obtiene para cortes grandes, o alturas de la caja mayores. Al modificar de forma dinámica el parámetro del “corte” mediante el deslizador del EV, los profesores pudieron reflexionar sobre algunas de sus hipótesis y franquear dicha idea previa.
Resultados
El uso del EV construido mediante un software de geometría dinámica, fue considerado por los profesores como un elemento motivante, sin embargo, se debatieron otros resultados de acuerdo al cuestionamiento planteado por el profesor guía: ¿qué posibles ventajas como desventajas tiene el uso de herramientas tecnológicas en la enseñanza de las matemáticas?
Con base en la experiencia realizada del uso de Geogebra y una secuencia didáctica para la introducción de máximos y mínimos en problemas de optimización, se llegó a acuerdos, de manera grupal:
-El uso de las tecnologías digitales por sí solas, no facilita la construcción y comprensión de los conceptos matemáticos, por ello, es necesario diseñar una cuidadosa secuencia didáctica que guíe al estudiante a la interiorización de los mismos.
-El uso de la herramienta permite realizar simulaciones, mover los objetos geométricos, contrario al lápiz y papel, donde se tornan estáticos. El resolver el problema mediante la construcción del EV, requiere de tener habilidades matemáticas, para llegar a la función apropiada, por lo tanto, el recrear el problema dinámicamente, permite al docente ser consciente de la importancia de las raíces de una función y el dominio, puesto que analíticamente la función obtenida presentaba un dominio que, para ciertos valores, no concordaba con la realidad presentada en el problema.
-No solo el uso de la herramienta tecnológica es un elemento motivante, sino el iniciar mediante un problema en contexto, y a partir de éste, explorar los significados de raíz de una función, dominio, y criterios de máximos y mínimos. En la resolución analítica se pudo corroborar que la población participante tiende al uso memorístico (Santos, 2003; Santos, 2010) de derivar una función e igualar a cero para luego hallar los máximos y mínimos, sin embargo, esta interpretación no siempre funcionó, puesto que algunas veces los máximos o mínimos se encuentran en los extremos del dominio de una función (Cuevas y Moreno, 2004).
En este caso mediante la construcción del EV, se propuso trazar la recta tangente a la función hallada V(x), y observar dinámicamente que, para un máximo del volumen, el valor de la pendiente de dicha recta tangente es igual a cero (de ahí el criterio), así como el dominio de la función es válido para valores acotados por las raíces (Figura 5).
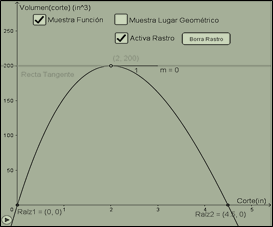
Figura 5. Pendiente de la tangente a la curva V(x) y puntos de corte obtenida en el EV. Fuente: Los autores
A pesar de las bondades ofrecidas por la herramienta digital, uno de los puntos de discusión, se basó en que la intensidad horaria invertida para el manejo y familiarización del software, es alta, lo cual, exige al profesor modificar las estrategias de enseñanza como prácticas pedagógicas, buscar espacios adecuados, y cambiar la planificación curricular.
Realizada una entrevista a estudiantes de los profesores sobre la estrategia implementada para su aprendizaje, permitió determinar categorías en torno al desempeño con características (Tabla 1).
Tabla 1. Categorías y análisis de desempeño del estudiante según entrevista.
|
Hallazgo |
Características |
Competencias |
|
Capacidad de Análisis |
Autocrítico, Argumentativo,
|
conceptualiza |
|
Síntesis |
Concentrado |
Organizar, extraer analiza, interpreta, concluye generaliza |
|
Productividad |
Independiente y Organizado
|
Da solución y una respuesta válida a interpretación de textos.
|
|
Comunicación |
Trabajo colaborativo, concreto y concertador, superación, apoyo, comunica |
Claro y conciliador. Expresa, lectura crítica pro-sociales |
|
Creatividad |
Motivación capacidad de trabajo, orientación al logro |
Desarrollo de habilidades y destrezas comunicativas Interpreta, crea, enseña. Desarrollo de nuevas heurísticas. |
|
Actitud |
Disfruta, interés, motivación, reflexiona |
Motivación |
|
Apoyo logístico social |
Bajos recursos, uso Tic solo en el colegio |
Crítica social |
Fuente: Autores.
Al igual que Arcavi & Hadas (2000), el uso escenarios dinámicos, permiten al estudiante construir figuras con propiedades y visualizarlas, así como transformar esas construcciones en tiempo real, y de esta manera se proveen herramientas que le permitan al estudiante justificar conjeturas y proposiciones. Dichas expresiones debatidas con profesores, fueron aceptadas, al mencionar que el uso de los EV son mediadores junto al trabajo del profesor, en el desarrollo de las actividades.
Capacidad de análisis, síntesis, productividad, comunicación, creatividad, actitud, apoyo logístico y social fueron categorías emergentes en programas replicados por los docentes participantes. Así mismo, se resalta el desarrollo de competencias pro sociales y actitudinales en el desarrollo de capacidad de tener buenas relaciones y una comunicación crítica, dentro de ambiente colaborativo en la generación de algoritmos y aprendizaje y enseñanza efectiva.
Conclusiones
El uso de la tecnología digital puede ser un factor motivante en la enseñanza de las matemáticas, permitiendo al estudiante la visualización de representaciones de los objetos matemáticos de manera dinámica. Sin embargo, la tecnología por sí misma no genera conocimiento, ni sustituye al profesor, por lo tanto, es necesario enmarcar las aplicaciones tecnológicas y en este caso los EV, dentro de una didáctica que promueva una comprensión y construcción de los conceptos matemáticos.
El incluir el uso de la tecnología digital en el currículo, exige al profesor modificar las estrategias de enseñanza, así como la planificación del curso. En el caso particular del uso de la tecnología, los EV influyen en la resolución de problemas por parte de los estudiantes, quienes posiblemente modifican sus heurísticas o formas de solucionar un problema, pero no es posible que el estudiante sea partícipe en la construcción del conocimiento o de un concepto matemático, si éstos escenarios virtuales no son acoplados dentro de una serie de actividades didácticas que orienten la actividad matemática del estudiante. Por lo anterior, el diseño y construcción de un EV en Geogebra, es una alternativa para que el profesor pueda implementar una práctica activa en el aula, bajo un diseño de actividades enfocadas a la comprensión de los conceptos en matemáticas.
Agradecimientos
A Centro de Investigación y de Estudios Avanzados del I.P.N. CINVESTAV-México, y Universidad Francisco de Paula Santander en la aceptación de proyecto FINU, A Jaime Rincón Leal por colaboración en traducciones, y a los profesores participantes, en especial a Edward Ortiz.
Referencias bibliográficas
Arcavi, A., y Hadas, N. (2000). Computer mediated learning: An example of an approach. International journal of computers for mathematical learning, 5(1), 25-45.
Bikner, A., Knipping C., y Presmeg, N. (Eds.). (2015). Approaches to Qualitative Research in Mathematics Education. Examples of Methodology and Methods. Dordrecht Heidelberg New York London: Springer. DOI 10.1007/978-94-017-9181-6.
Cuevas, C., y Moreno, S. (2004). Interpretaciones erróneas sobre los conceptos de máximos y mínimos en el Cálculo Diferencial. Educación Matemática. Redalyc, 16(002), 93-104.
Cuevas, C.A., y Pluvinage, F. (2003). Les projets d'action practique, elements d'une ingeniere d'ensigment des mathematiques. Annales de didactique et de sciences cognitives, 8, 273-292.
Cuevas, C.A., Rodríguez, A., y González, O. (2014). Introducción al concepto de derivada de una función real con apoyo de las tecnologías digitales. Revista el Cálculo y su enseñanza. 5, 149-156. Disponible en línea: http://mattec.matedu.cinvestav.mx/el_calculo/index.php?vol=5&index_we b=11&index_mgzne.
Cuevas, C.A., y Villamizar, F. Y. (septiembre del 2015). Propuesta didáctica para la enseñanza de las cónicas mediante un entorno digital interactivo. En: J. Alba (compilador), Memorias Congreso Internacional de Didáctica de la Matemática. Una mirada epistemológica y empírica, (pp. 203-221), Santa Marta: Colombia.
Cuevas C.A., Villamizar, F.Y., y Martínez, A. (2017). Aplicaciones de la tecnología digital para actividades didácticas que promuevan una mejor comprensión del tono como cualidad del sonido para cursos tradicionales de física en el nivel básico. Enseñanza de las Ciencias, 35(3), 129-150. https://doi.org/10.5565/rev/ensciencias.2091.
Duval, R. (1998). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En F. Hitt (trad.), Investigaciones en matemática educativa II (173-201). México: Iberoamérica.
Granville, W.A. (2017). Cálculo diferencial e integral. México: Limusa.
Hohenwarter, M. (2018). GeoGebra. Disponible en: https://www.geogebra.org/.
National Council of Teachers of Mathematics (Ed.). (2000). Principles and standards for school mathematics (Vol. 1).
Purcell, E. J., Rigdon, S. E., & Varberg, D. E. (2007). Cálculo (novena edición). México: Pearson Educación.
Santos, L. M (2003). Procesos de Transformación de Artefactos Tecnológicos en Herramientas de Resolución de Problemas Matemáticos. Boletín de la Asociación Matemática Venezolana. 10(2). 195-211.
Santos, L. M. (2010). La resolución de problemas matemáticos: fundamentos cognitivos. México: Trillas.
Serres, M. (2014). Pulgarcita. México: Fondo de Cultura Económica.
Stake, R., E. (1999). Investigación con estudio de casos (segunda edición). Madrid: Morata.
Vergel Ortega, M., Rincón Leal, O y Zafra, S. (2017). Influencia del curso precálculo en ecuaciones diferenciales y desarrollo del pensamiento variacional. En: Pedagogía y construcción de ámbitos en educación. Estados Unidos: Redipe, 646-660.
Vergel Ortega, M., Rincón Leal, O y Salazar, J.P. (2017). Perspectivas y pensamiento matemático desde las comunidades de aprendizaje. En: Prácticas Pedagógicas. Venezuela: Publicaciones científicas Universidad del Zulia, 1000-1013.
Villamizar, F.Y. (2017). Problema de optimización-Caja de máximo volumen. Recuperado el 21 de septiembre del 2017. Disponible en: https://www.geogebra.org/m/vETBV5bQ