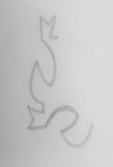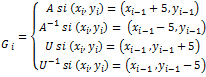Patrones en mosaicos Y
Teselados desde Composiciones Geométricas*
Patterns in Mosaics and
Tessellations from Geometric Compositions *
Padrões em Mosaicos e Tessellations de
Composições Geométricas *
Innias Miguel Cadena
González**
Mawency Vergel Ortega***
Julio Alfredo Delgado
Rojas****
Universidad Francisco De Paula Santander- Colombia
Fecha
de recepción del artículo: 13 de agosto de 2017
Fecha de aceptación del artículo: 18 de marzo de 2018
Fecha de Publicación: 01 de Abril de 2018
DOI:
http://dx.doi.org/10.22335/rlct.v10i2.569
*Articulo
resultado de la investigación “Geometrización de indicadores urbanos como
herramienta didáctica para el desarrollo de competencias investigativas en
estudiantes de arquitectura” enmarcada en la línea de investigación matemática
aplicada de la Maestría en Educación Matemática- grupo
Euler, desarrollada con apoyo de asignaturas Taller de Diseño y,
matemáticas, geometría y arquitectura del programa Arquitectura de la
Universidad Francisco de Paula Santander.
**
Arquitecto en formación. Filiación: Universidad Francisco de Paula Santander.
Correo electrónico: miguel_cadena25@hotmail.com. Orcid ID: https://orcid.org/0000-0002-3616-3077
***Maestrante
en Educación Matemática, Arquitecto. Filiación: Universidad Francisco de Paula
Santander. Correo electrónico: julioalfredo@ufps.edu.co Orcid ID: https://orcid.org/0000-0001-6944-832X
****Doctora
en Educación. Postdoctora en Imaginarios y representaciones sociales.
Filiación: Universidad Francisco de Paula Santander. Correo electrónico: mawency@ufps.edu.co. Orcid ID: https://orcid.org/0000-0001-8285-2968
____________________________________________________
Resumen
La investigación tiene
por objeto geometrizar indicadores del espacio público. A partir de una metodología
de diseño geométrica se generaron teselas que respondieran a la lógica
matemática, y conservara un carácter artístico asociado a la cultura de la
región de frontera, al encargarse de estudiar la cualidades y propiedades de
las formas que se pueden encontrar en el espacio habitable o en ejercicios
teóricos matemáticos. Resultados presentan una composición geométrica definida
como teselado utilizada para recubrir distintos planos. Conclusión: La
exploración de formas y figuras presenta como resultado un teselado apropiado a
la cultura de la ciudad de Cúcuta, el cual comprende dos piezas articuladas
para formar un mosaico que responde a la lógica de diseño inspirada en M. C.
Escher.
Palabras clave:
mosaico, teselado, composición geométrica
Abstract
The
Geometry, in charge of studying the qualities and properties of the forms that
can be found in the habitable space or in mathematical theoretical exercises,
can be used as a tool to generate mosaics or tessellations that respond to a
mathematical logic, at the same time maintaining an artistic kind. Its
usefulness can be manifested for various contexts for which a geometric
composition defined as tessellation that can be used to cover different planes
is presented in this article. After the exploration of shapes and figures using
a geometric design methodology, a tessellation is presented as a result of two
pieces that are articulated to form a mosaic responding to a design logic
inspired by M. C. Escher.
Keywords:
mosaic, tessellation, geometric composition
Resumo
A geometria, encarregada
de estudar as qualidades e propriedades das formas que podem ser encontradas no
espaço vivo ou em exercícios teóricos matemáticos, pode ser usada como
ferramenta para gerar mosaicos ou telhas que respondem a uma lógica matemática,
mantendo ao mesmo tempo uma personagem artístico. Sua utilidade pode ser
manifestada para vários contextos para os quais uma composição geométrica
definida como tesselagem que pode ser usada para cobrir diferentes planos é
apresentada neste artigo. Após a exploração de formas e figuras usando uma
metodologia de design geométrico, é apresentada uma tesselação como resultado por
duas peças articuladas para formar um mosaico que responde a uma lógica de
design inspirada por M. C. Escher.
Palavras-chave:
pensamento crítico, violência no namoro adolescente, estudo de caso
Introducción
Los mosaicos y teselados
han servido como un juego de patrones con tendencias artísticas que suelen ser
utilizados en distintos contextos como azulejos para pisos, baldosas o murales,
cuadros y en algoritmos matemáticos o diseños arquitectónicos.
Los teselados se pueden
presentar como arte gráfico el cual mantiene relaciones matemáticas intrínsecas
en las que podemos encontrar formas básicas como teselaciones en triángulos,
cuadrados o hexágonos que se van modulando en un plano, hasta figuras más
complejas como animales, rostros o expresiones abstractas geometrizadas. Las
teselaciones pueden presentar una infinidad de posibilidades en su
configuración, en las que se pueden catalogar como: teselaciones regulares (en
el que todos son iguales), teselaciones irregulares (caracterizadas por la
utilización de dos o más polígonos regulares) teselaciones periódicas (que
recubre un plano de manera periódica) y teselaciones aperiódicas (recubren un
plano, pero no de manera periódica).
El artículo tiene por
objetivo diseñar un mosaico a partir de técnicas geométricas para generar una
composición por medio de patrones y expresiones matemáticas, para ello se
identificaron estrategias de diseño para generar mosaicos o teselas, se
estableció un proceso de diseño para un mosaico, se mostró un nuevo diseño de
una tesela para generar un mosaico artístico geométrico, a partir de ello se
presenta un diseño generado a través de una teselación periódica, combinó la
exactitud geométrica con lo dinámico de las formas orgánicas, inspiradas en los
dibujos de M. C. Escher, se muestra como resultado un mosaico que comprende dos
teselas o módulos, que se articulan de manera irregular, pero con tendencia
periódica, con un carácter paramétrico para poder replicar en distintas
propuestas de desarrollo de recubrimientos.
Antecedentes presentan
teselados a través de la historia en distintas culturas para generar arte o
recubrir espacios como vías, o incluso en sistemas constructivos en los que se
pueden encontrar como referentes los sumerios, romanos, estudios de Arquímedes
en el siglo III a.c. o en obras teóricas como “Harmonice mundi” de
Johannes Kepler en 1619 (Mariño, 1938), o incluso un ejemplo del siglo XX fueron
los trabajos del artista holandés M. C. Escher (1898 – 1972), en los cuales las
técnicas de su aplicación son diversas pero cada manifiesta por transeúntes y
habitantes es interesante visualmente, y su correspondencia geométrica ha sido
muy útil a la hora de estudiar las distintas propiedades de una figura
geométrica.
Metodología
La construcción y diseño
siguió enfoque de una metodología de diseño geométrica basada en las técnicas
de dibujo de teselas empleada por el artista M. C. Escher (figura 1).
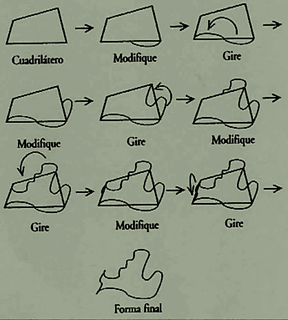
Figura 1. Teselado de
Escher. Fuente: Escher, 2008
Así una región con
N cuadrados tiene T teselaciones, y 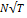 grados de libertad por cuadrado.
grados de libertad por cuadrado.
Se generan bocetos
de diseño (a) en Figura 2, los cuales expresaron de manera empírica las figuras
que pueden aparecer a medida que el trazado se generó b (Figura 2) a través del
contraste entre las tonalidades de claro y oscuro, y a partir de los supuestos
de Thurston (1990) para toda región R sin agujeros, toda teselación con dominós
de R puede lograrse a partir de cualquier otra por medio de una sucesión de giros.
No obstante, la región de regularidad no se aproxima a la frontera de un
círculo tangente a los cuatro lados fronterizos.
Se mantiene
entonces con la simplicidad de trabajar con figuras sencillas y complejizarlas
a medida que se superponen planos semilla 1 y 2 b,c,d en (Figuras 2) se trabaja
la forma resultante (Figura 3). Se busca a partir de este patrón generar una
simetría inmersa en grupos cristalográficos planos, sin embargo, aún, la región
de regularidad no se aproxima a la frontera de un círculo tangente, por lo cual
se recurrió a teselaciones no simétricas o teselaciones de Penrose las cuales
tienen propiedades notables; como el contener una cantidad infinita de copias
de cualquier región finita que uno pueda formar usando las figuras.
el plano al
utilizar las figuras con la condición que solo se pueden unir en vértices que
tengan el mismo ángulo hace imposible cubrir el plano repitiendo un patrón
pequeño en forma regular, como se hizo en las teselaciones anteriores. Sin
embargo, existen infinitas teselaciones del plano usando flechas y cometas.
La rotación en 60º
de un patrón triangular modificado, generó un patrón basado en un hexágono
regular. La construcción del patrón consistió en construir una línea mn y
rotarla en 60º. En éste caso, el arco rs, se rota en 60º alrededor de s. Luego
se construye el punto medio (M) de rr’, se construyó una línea que una r y M; y
finalmente se aplica simetría central de dicha línea respecto a M. Como
consecuencia, las líneas construidas, determinan un patrón que permite teselar
con rotaciones en 60º. Los puntos r, s y r’, determinan un triángulo
equilátero. Alrededor del punto O se ha girado sucesivamente el patrón en 60º,
de manera que los triángulos equiláteros determinan un hexágono regular (d) en
(Figura 2.).
De otra parte, acorde
a la teoría Walkup [26] mostró que un rectángulo de r x s puede ser
perfectamente mosaico por T-tetrominoes si y solo si r = s = 0 (mod 4). Se
puede comprobar que tales rectángulos tienen Tiques tetrominios firmados si y
solo si rs - 0 (mod 8). Por lo tanto, esto problema tampoco puede ser resuelto
por un argumento colorante o de ángulos generalizado. El argumento de Walkup es
especial para el T-tetromino; su relación con el enfoque de la teoría de grupos
combinatoria de este documento no es obvio. Los invariantes de límites
definidos pueden, en principio, ser definidos para mosaicos en subregiones
finitas de cualquier mosaico periódico de w2 o de hiperbólico espacio W "
(Walkup, 1965).
|

a
|
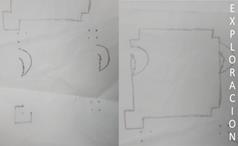
Exploración de formas que se repitan en un juego de contrastes
y figuras
 
b
|
|

c
|

d
|
Figura 2. Exploración de
formas, traslación y rotación. Fuente: Autores
El punto d en Figura 2 es
considerado un snub de {3,6} uniforme con símbolo [0](12)(34).(3,6,3,3,3) que
codifica un grafo  (Godman y Slone, 2018; Blatov, Shevchenko
& Proserpio, 2014)
(Godman y Slone, 2018; Blatov, Shevchenko
& Proserpio, 2014)
Se aplicó traslación a
extremos de un cuadrado (todo lo que se quita en un extremo se traslada al
otro). como un principio de conservación deformando un objeto a partir de
cuatro movimientos y se traslada en 5 unidades hacia arriba (a) en (Figura 3).
Se aplica e interpreta la
técnica de Escher, para dar lugar a una figura controlada fácil de entender
(Figura 4, 5).
El diseño tiene en cuenta
postulados de Conway y Lagarias (1990), quienes afirman que al camino P = {(xi
, yi): 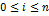 ) se asigna un W = W
(P)=Gn, Gn-1, …,G1 en F dado por,
) se asigna un W = W
(P)=Gn, Gn-1, …,G1 en F dado por,
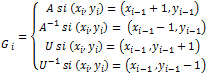
Donde A representa el
conjunto de todas las traslaciones a través de presentes en un mosaico en una
región R y un conjunto de∑tipos de mosaicos. R puede ser cubierto por dos
patrones si existe un conjunto en Z que cubre cada céda en C de R exactamente
una vez. U el conjunto de traslaciones hacia arriba. En el mapeo en la
dirección inversa se asigna a cada W en F la trayectoria dirigida P(W) a partir
de la base fija en el cuadrante en (0, 0) en Z2 obtenido al observar
la figura en W de derecha a izquierda, y se tiene W(P (W))=W. Dado un límite
orientado 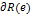 de una región R
simplemente conectada,
de una región R
simplemente conectada, 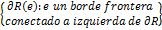 , permutaciones cíclicas
entre sí, conjugadas en F para las regiones en la figura 3h y subregión de
filas en figura 5,
, permutaciones cíclicas
entre sí, conjugadas en F para las regiones en la figura 3h y subregión de
filas en figura 5, 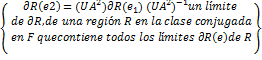 es decir,
es decir,
[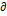 R]
= {W
R]
= {W  R (e) W-1:
WE F}.
R (e) W-1:
WE F}.
El grupo: (W1,
W2, .. ..) denota un subgrupo G de F, G N(G)
subgrupo más pequeño en F, [G: G] denota el subgrupo generado por los
conmutadores W1W2W1-1W2-1,para
todo W1,W2,
N(G)
subgrupo más pequeño en F, [G: G] denota el subgrupo generado por los
conmutadores W1W2W1-1W2-1,para
todo W1,W2, 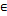 G. (Harpe, 2000). El
grupo de ciclo C es el subgrupo libre de F que consiste en todas las
palabras asociadas a rutas dirigidas cerradas en la cuadrícula cuadrada. límite
combinatorio de cualquier región simplemente conectada está contenido en
C=[F:F´].
G. (Harpe, 2000). El
grupo de ciclo C es el subgrupo libre de F que consiste en todas las
palabras asociadas a rutas dirigidas cerradas en la cuadrícula cuadrada. límite
combinatorio de cualquier región simplemente conectada está contenido en
C=[F:F´].
Los argumentos de coloración
o ponderación corresponden a invariantes aditivos asignados a las celdas de la
cuadrícula cuadrada. El siguiente teorema mostró que un grupo natural que
codifica tales invariantes es el máximo grupo cociente abeliano A0
= C / [C: C], o célula de grupo.
Teorema: El ciclo grupo C
consiste en todas las W tales que P(W) es cerrado en Z *, es decir, C = [F: F].
El grupo [C: C] consiste en todas las W tales que P (W) es una trayectoria
directa cerrada en Z2 con 0 alrededor de cada celda en Z2.
En consecuencia, [C: C] es un subgrupo normal de F. El grupo A0 =C/[C:C]
es una suma directa de un número contable de copias de Z,las cuales tienen
correspondencia uno a uno con las celdas cii de Z2. 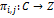 sobre la cijth
Z-sumando de A0 está dado por w(P(W);cij) (Conway y
Lagarias, 1990)
sobre la cijth
Z-sumando de A0 está dado por w(P(W);cij) (Conway y
Lagarias, 1990)
El diseño toma referentes
de Teorema “un triángulo equilátero con huecos puede ser teselado con rombos si
y sólo si cada triángulo de lado k contiene a lo más k huecos (Ardila, Billey,
2005) para producir matroides a partir de emparejamientos en las teselas y la
reflexión del patron semilla final. Estas teselaciones son las subdivisiones
mixtas de triángulos definidas en el contexto de politopos y variedades teóricas,
y están relacionadas con problemas de optimización y geometría tropical. De
igual manera b y c en figura 4 y Figura 5 se generan a partir de de d banderas.
Una vez se determinó la
forma de diseño se generó un nuevo módulo (Figura 4), el cual se diseñó a
partir de iteraciones de movimientos de extremos que le otorgaron complejidad,
al mantener la lógica de la sustracción de un lado del polígono y la suma a
otra parte del mismo polígono con bordes encajables en puntos límite. c en
(Figura 4, figura 5).
La iteración del diseño a
partir de traslación de puntos generó un mosaico en el plano (Figura 6, Figura 7),
por lo que se procedió a generar una cuadrícula ligada a un diseño inicial de
forma orgánica como representación artística enfocada al dibujo.
A fin de obtener una
figura geométrica asociada a la cultura de la región a partir del patrón
diseñado, se procedió a cambiar la escena del dibujo y al mismo tiempo a
moldear la figura geométrica para representar el mismo concepto de orgánico en
la ensena de animales de granja en dos contextos basados en contrastes de
color. Del diseño se presentaron dos piezas irregulares, pero complementarias
en el plano, de tal manera que se intersectan en los puntos frontera. Las dos
presentan escenas distintas, la primera inspirada en un amanecer, y la segunda
en un anochecer, generando así dos teselas para presentar el mosaico final.
Se demuestran en la
tesela final argumentos de interpretación natural en términos de invariantes de
límites y donde los argumentos más fuertes son equivalentes a la detección la
existencia de mosaicos firmados. Considerada la cuadrícula cuadrada con su
grupo libre asociado F = (A, U) y un ciclo grupo C = [F: F]. Los argumentos de
coloración claro oscuro corresponden a invariantes aditivos asignados a las
celdas de la cuadrícula cuadrada. Parte de teorema muestra que un grupo natural
que codifica tales invariantes es el máximo grupo cociente abeliano A, = C /
[C: C], célula grupo. (Conway y Lagarias, 1990)
Teorema (i) El ciclo
grupo C consiste en todas las W tales que P (W) es un camino dirigido cerrado
en Z *, es decir, C = [F: F]. (ii) El grupo [C: C] consiste en todas las
palabras W tales que P (W) es una trayectoria directa cerrada en Z2 con el
número de cuerda 0 alrededor de cada celda en Z2. En consecuencia, [C: C] es
un subgrupo normal de F (Conway & Lagarias, 1990).
Figura 3. Semilla 3- Fuente:
Autor
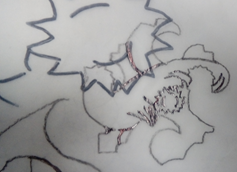
Figura 4. Construcción
Tesela 1. Fuente: Autor
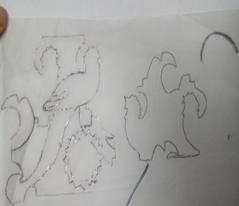
Figura 5. Traslaciones e
Iteraciones para generar figura asociada al campo
Resultados
De acuerdo al proceso de
diseño se logran concretar dos módulos (uno de mayor proporción que el otro)
los cuales se presentan como teselado irregular de tipo periódico, con imágenes
orgánicas, generan así una nueva propuesta de mosaico del cual se realizan la
modelación en 3D, a escala real en material de cartón, para poder ver los
atributos de la figura y su factibilidad a la hora de teselarse. con
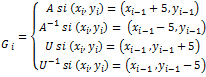
La tesela en mosaico en
plano R, sigue secuencia de 346 estuvo dada por a(0)=1, a(1)=5,
a(2)=9, a(3)=15, a (4)=19, a(5)?24 a(n)=a(n)+24. La recurrencia se puede
escribir como a (5k + r) = 24k + a (r) para k ≥ 0, 0 ≤ r ≤ 16 a partir de snub
{6,3} con grupo de simetría 632.
Los resultados se
presentan por medio de un dibujo a base de carboncillo, en el que se logra
apreciar la composición completa del diseño en el que se recuperan los
conceptos de Escher de poder visualizar dos escenas, pero no al mismo tiempo,
pues el reflejo de una es gracias al contraste de la otra (figura 7).
El resultado final es un
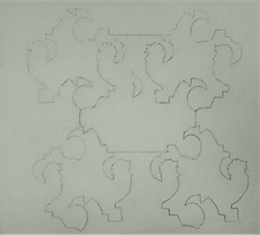
mosaico orgánico (Figura 8) con una escena nocturna y una de día en la que el
principal protagonista es un ave, generándose una interesante composición que
une el arte y la geometría
Figura 6. Reflexión,
figura granja para construcción mosaico. Fuente: Autor
Figura 7. Patrón y
Tesela resultante
Figura 8. Mosaico.
Fuente: Autor
Discusión
y conclusiones
De acuerdo al trabajo
realizado, se puede afirmar que las estrategias de diseño de un mosaico
permiten infinidad de teselas o figuras al seguir parámetros de diseño y
lineamientos de traslaciones, rotaciones, reflexiones, grupos de Lie, donde la
geometría no se limita a permitir generar líneas rectas o teselas regulares,
planteadas por figuras básicas, sino patrones irregulares complejos
generadores de obras de arte y de igual manera, permite apreciar la destrezas,
habilidades, competencias frente a la técnica del autor similar a resultados de
Souza, & Marafioti (2013) y de Herrera, et.al. (2010) partir de otras
experiencias en aula. Así mismo, al igual que Hernández y Rojas (2016) es
posible generar modelos y analizar estructuras topológicas.
Se
logran determinar frente al estudio investigativo distintas estrategias de
diseño, en las que se logran determinar unas teselas regulares, irregulares,
periódicas, y aperiódicas, que esto no limita para generar combinaciones entre
estas técnicas, e involucrar formas orgánicas en la obra.
Se generó a partir de dieciséis movimientos en el plano el patrón
irregular de la tesela, un resultado tangible que permite visualizar que las
teselas pueden presentarse en azulejos aplicados a distintos contextos culturales
en terminaciones arquitectónicas, obras de arte o pintura.
Referencias
bibliográficas
Bailey, D. Cairo
Tiling, recuperado de http://www.tess-elation.co.uk/cairo-tiling.
Blatov,
A., Shevchenko, P. & D. M. Proserpio, (2014). Applied topological analysis
of crystal structures with the program package ToposPro, Cryst. Growth Des.,
14, 3576-3586.
Conway,
J.H. & Lagarias, J.C. (1990). Tiling whit polyminoes and combinatorial
group theory. Journal of combinatorial theory. 53. 183-208
de
Souza, L. A., & Marafioti Garnica, A. V. (2013). The modern math
movement(s): An essay on how elementary school teachers in brazil gave meaning
to it. [As
matemáticas modernas: Um ensaio sobre os modos de produção de significado ao(s)
movimento(s) no ensino primário Brasileiro] Revista Latinoamericana De
Investigacion En Matematica Educativa, 16(3), 369-393.
doi:10.12802/relime.13.1634
Escher M.C, (2008).
Estampas y dibujos. Introducción y comentarios de M.C. Escher. Ed. Taschen.
Gómez-Jáuregui V., Otero
C., Arias R. and Manchado C. (2011). Generation and
Nomenclature of Tessellations and Double-layer Grids.
 Goodman-Strauss,
C. & Sloane, N.J.A.. (2018). A coloring book approach to finding
coordination sequences. Arxiv. 1. New York: Cornell University Library.
Goodman-Strauss,
C. & Sloane, N.J.A.. (2018). A coloring book approach to finding
coordination sequences. Arxiv. 1. New York: Cornell University Library.
Harpe,
P. (2000). Topics in Geometric Group Theory. Chicago: Univ. Chicago
Press.
Hernández,
M. M. V., & Rojas, E. M. (2016). Determinants of academic performance in
mathematics in the context of a technological university: Application of
structural equations model. [Factores que determinan el
rendimiento académico en matemáticas en el contexto de una universidad
tecnológica: Aplicación de un modelo de ecuaciones estructurales] Universitas
Psychologica, 15(4), 1-11. doi:10.11144/Javeriana.upsy15-4.fdra
Herrera V., Montes, Y.,
Cruz C., Vargas A. (2010) Teselaciones: Una Propuesta para la
Enseñanza y el Aprendizaje de la Geometría a Través del Arte. Bogotá:
Universidad Distrital Francisco José de Caldas.
Mariño, S. (1938). Geometría
en el arte y el diseño. Bogotá: Universidad Nacional.
Walkup, D. (1965). Covering
a rectangle with T-tetrominoes, Amer. Math. Month!v . 72. 986-988.
![]()

![]() grados de libertad por cuadrado.
grados de libertad por cuadrado. 




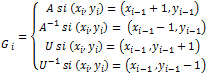
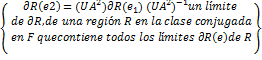

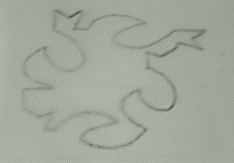
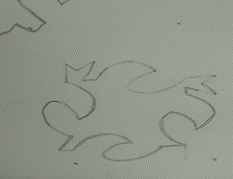
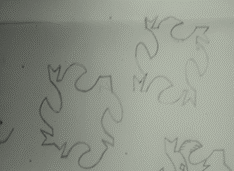


 g
g h
h