Fecha de Recibido: Enero 24 del 2017
Fecha de Aceptación: Marzo 03 de 2018
Fecha de Publicación: Abril 01 de 2018
DOI: http://dx.doi.org/10.22335/rlct.v10i2.557
*El artículo resultado de la investigación “Una propuesta para introducir el pensamiento funcional y el concepto de función real, antes de un curso de cálculo diferencial”, nace de la reflexión sobre la problemática en la enseñanza del Cálculo, debatida por diversos investigadores de universidades de México, España, Inglaterra, Francia y Colombia, en el Seminario Internacional de Enseñanza del Cálculo impartido en el CINVESTAV.
**Doctor en Ciencias en la especialidad de Matemática Educativa e investigador titular en el Departamento de Matemática Educativa-CINVESTAV, miembro de la Academia Nacional de Ciencias-México. Filiación: Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México Departamento de Matemática Educativa. Correo electrónico: ccuevas@cinvestav.mx . Orcid ID: https://orcid.org/0000-0002-7529-4520
***Doctor en Ciencias y matemático puro. Filiación: Universidad Nacional de Educación a Distancia, España Correo electrónico: miguel@mat.uned.es Orcid ID: https://orcid.org/0000-0001-9550-0427
****Doctora en Ciencias en la especialidad de Matemática Educativa del CINVESTAV, Filiación: Centro Universitario UAEM Valle de Chalco, México. Correo electrónico: mmartinezr@uaemex.mx Orcid ID: https://orcid.org/0000-0002-2643-6748
_____________________________________________________________________________________________
Resumen
El artículo muestra que un factor importante en el fracaso de los estudiantes en el primer curso de cálculo diferencial, es la carencia del concepto de función. Esto no es sorprendente puesto que diversos reportes de investigación muestran la complejidad de este concepto en diferentes niveles educativos. La investigación tuvo como objetivo incorporar al inicio del curso de cálculo un reforzamiento del pensamiento matemático básico, al incluir el pensamiento funcional. Para validar el modelo se aplicaron a una muestra de 45 estudiantes, actividades didácticas que promovieron el pensamiento matemático; resultados muestran un grado de desarrollo aceptable de pensamiento funcional y logro asociados a aprobación del curso de cálculo. Se evidenció que el diseño de actividades didácticas basadas en esta propuesta promueve sustancialmente la comprensión del concepto de función real.
Abstract
This article shows that an important factor in the failure of students in the first course of differential calculus is the lack of the concept of function. This is not surprising since several research reports show the complexity of this concept in different educational levels. It is proposed to start the course of calculation with a reinforcement of basic mathematical thinking, including functional thinking. We present evidence that the design of didactic activities based on this proposal substantially promotes the understanding of the concept of real function. To validate, we apply to 45 students, didactic activities that promote mathematical thinking; achieving an acceptable degree of functional thinking to bring the course of calculation to a good conclusion.
Keywords: real function, functional thinking, variation, epistemological analysis, digital technology
Resumo
Esta pesquisa mostra que um fator importante na falha dos alunos no primeiro curso do cálculo diferencial é a falta do conceito de função. Isso não é surpreendente, pois vários relatórios de pesquisa mostram a complexidade desse conceito em diferentes níveis educacionais. Propõe-se iniciar o curso do cálculo com um reforço do pensamento matemático básico, incluindo o pensamento funcional. Apresentamos evidências de que o desenho de atividades didáticas com base nesta proposta promove substancialmente a compreensão do conceito de função real. Para validar, aplicamos a 45 alunos, atividades didáticas que promovem o pensamento matemático; alcançando um nível aceitável de pensamento funcional a fim de trazer o curso de cálculo para uma boa conclusão.
Palavras-chave: função real, pensamento funcional, variação, análise epistemológica, tecnologia digital.
Introducción
Uno de los más evidentes problemas de la enseñanza de la matemática, a nivel medio superior y superior, es el bajo aprovechamiento en un primer curso de cálculo diferencial e integral (Attorps, Björk y Radic, 2016; Benacka y Ceretkova 2013; Blanco, Cárdenas, Figueiredo y Contreras, 2014; Bloch 2003, Kjeldsen y Petersen 2014; Lagrange 2014; Vargas, Reyes y Escalante, 2016; entre otros.). Como el cálculo es el estudio de las funciones (Luzin 1998, 428), una de las razones más importantes de esta falla lo constituye el hecho de que, en general, los estudiantes no poseen un significado aceptable del concepto de función real. Aún más, en diversos estudios diagnósticos, realizados por los autores, se ha detectado que la mayoría no alcanza un pensamiento funcional y, en consecuencia, al aprender los diversos conceptos del cálculo se tiene una deficiente o incompleta comprensión de estos.
Adicionalmente, como función es la relación matemática más importante para modelar matemáticamente fenómenos de las diversas ciencias naturales y sociales (Spivak, 1967; Kjeldsen y Lützen 2015; Blanco et.al., 2014), el no tener una aceptable comprensión de este concepto impide una mejor comprensión de los hechos propios de las diversas ciencias.
A partir de Galileo Galilei (1981) se estableció el indisoluble vínculo entre las ciencias naturales y la matemática, e indudablemente la modelización matemática de los fenómenos naturales contribuyó a desvelar muchos de los misterios de la misma naturaleza. Relaciones como:
•
, (1)
relación que expresa la velocidad de un móvil en un movimiento uniforme con
aceleración a, velocidad inicial y tiempo t.
•
, (2)
enuncia la reproducción de una población, en donde t representa los periodos de
reproducción transcurridos. P0 es la población inicial (cuando t=0), r es la
tasa porcentual de crecimiento (decrecimiento) por periodo de reproducción.
Estas dos relaciones, de muchas más, muestran en efecto, que como Galileo afirmaba (Kjeldsen y Lützen, 2015), el lenguaje de las ciencias es la matemática y de ella, uno de los instrumentos o conceptos más importantes es el de función. Los términos: variable, parámetro, número, variación y cantidad, son conceptos abstractos; y precisamente la modelización matemática de diversos fenómenos naturales y sociales que establece la función, no sólo da significado a estos conceptos, sino que, además, establece una relación entre dichos conceptos básicos.
Pensamiento matemático básico
El desarrollo del pensamiento matemático básico se puede establecer desde el punto de vista cognitivo en las siguientes etapas:
•Pensamiento aritmético.
•Pensamiento aritmético avanzado (proporciones).
•Pensamiento algebraico.
•Pensamiento funcional.
El pensamiento aritmético corresponde al conocimiento de los números y operaciones aritméticas básicas (Kjeldsen y Petersen, 2014; Mouhayar y Jurdak, 2016). La segunda etapa, pensamiento aritmético avanzado, se refiere a un conocimiento numérico más avanzado; esto es, a partir de las operaciones aritméticas básicas se desarrollan las proporciones y el manejo de fracciones; incluye también, el conocimiento de magnitudes y elementos de razonamiento lógico (Pluvinage y Cuevas, 2006). La tercera etapa, el pensamiento algebraico, incluye reconocer y analizar patrones, estudiar y representar relaciones, hacer generalizaciones y analizar cómo cambian las cosas. También contiene los sistemas matemáticos de signos (SMS); la resolución de ecuaciones y el manejo de expresiones que incluyen variables y parámetros. Es conveniente señalar que la adquisición de este pensamiento facilitaría la comprensión del simbolismo abstracto y el trabajo con relaciones algebraicas (Filloy, Puig y Rojano, 2008; Lagrange 2014; Seeley 2004).
La última etapa, pensamiento funcional, es una actividad cognitiva, una etapa del desarrollo del pensamiento matemático que permite establecer relaciones de dependencia funcional, más allá de las relaciones aritméticas y algebraicas que pueden ser aplicadas a diversos contextos. Aún más, se considera que para poder interactuar en el mundo actual y poder desarrollarse en cualquiera de las diversas disciplinas o ciencias tanto básicas, naturales como sociales, se requiere de un pensamiento funcional (Pluvinage y Cuevas, 2006).
Una vez definidos estos tipos de pensamiento, surge la siguiente cuestión: ¿Cómo desarrollar actividades para promover un pensamiento funcional? Lo que conduce a la cuestión primaria: ¿Cómo promover un aprendizaje del concepto de función en los estudiantes?
Por supuesto que por pensamiento funcional no se refirió a la repetición verbal de la definición de función, institucionalizada por los diversos libros de texto; una definición considerada compleja y sofisticada por la amplitud que desea obtener, cuando para los propósitos de un primer curso de cálculo se partió de una definición más sencilla referente a una relación funcional entre dos números reales y en el tiempo irle agregando propiedades y complejidad.
Enseñanza del concepto función real
El concepto de función es de los primeros temas a tratar en los libros de texto de análisis matemático o cálculo y uno de los conceptos más analizados en la investigación educativa (Kleiner, 1989; Luzín, 1998; Mesa, 2004; Vergel, Rincón y Zafra, 2017). Aún más, en muchos programas educativos se incluye desde el nivel secundaria (Programas, 2016).
El concepto de función es un “concepto unificador en matemáticas” y “el lenguaje de las matemáticas” se utiliza para describir el concepto de función en la formación matemática en la etapa básica, según lo formulado por el Consejo Nacional de Maestros de Matemáticas (NCTM 1989). “El cambio y la causalidad se expresan mediante el simbolismo de las funciones” (NCTM 2012, 51).
Para lograr la concepción de función real actual fue necesario establecer una teoría del continuo coherente, lo cual como es conocido no se logró formular hasta la aparición de los trabajos de Cantor (Kleiner 2012, 123; Kjeldsen y Lützen, 2015) a principios del siglo XX. Por esta razón, la concepción de función más común, para profesores y libros de texto actuales, es una consecuencia del desarrollo histórico del concepto y del posicionamiento filosófico que los matemáticos impulsaron desde 1900, concerniente a los fundamentos de la matemática (Mesa, 2004). Dado que gran parte de las praxeologías del medio docente establece su marco de referencias y sus creencias, en base a las definiciones de los libros de texto institucionales, se expone una pequeña muestra de los libros de texto más usuales en los primeros cursos universitarios, que pueden revelar el origen de ciertas creencias y prácticas docentes para el tratamiento que se le da al concepto de función (Kjeldsen y Lützen, 2015; Blanco et. al. 2014; Mesa 2004).
•Una función de X a Y es una regla (o método) para asignar un (y sólo un) elemento de Y a cada elemento de X, donde se aclara que, por lo general, X e Y son conjuntos de números reales (Stein y Barcellos 1995, 13).
•Una función f es una regla que asigna a cada elemento x de un conjunto A exactamente un elemento, llamado f(x), de un conjunto B. Además, se consideran funciones para las cuales los conjuntos A y B son conjuntos de números reales (Stewart 2001, 12).
•Sean X e Y dos conjuntos de números reales. Una función real f de una variable real x de X a Y es una correspondencia que asigna a cada número x de X exactamente un número y de Y (Larson, Hostetler y Edwards 1999, 25).
•Una función F es un conjunto de pares ordenados (x, y) ninguno de los cuales tienen el mismo primer elemento. Esto es, si (x, y) pertenece a F y (x, z) pertenece a F, entonces y=z (Apostol 1996, 42).
•Una función es una colección de parejas de números con la siguiente propiedad: Si (a, b) y (b, c) están ambas en la colección, entonces b=c. En otras palabras, la colección no puede contener dos parejas distintas con la misma primera coordenada. (Spivak 1967, 60).
De la mayor pare de los textos analizados se observa que las definiciones mostradas son idénticas, una de la otra, salvo por ligeras modificaciones del lenguaje. Además, son extremadamente generales y utilizan un lenguaje matemático formal, cuando lo que se desea, en los cursos de cálculo o precálculo, es trabajar solo con funciones reales. Como señalan Bloch (2003), Díaz (2007) y Luzín (1998), entre otros, las razones por las cuales los estudiantes tienen dificultades con el concepto de función parecen centrarse en su complejidad y generalidad, ya que presenta muchas facetas y contiene una multiplicidad de representaciones. Para fijar ideas acerca de las prácticas docentes, señalaremos algunos ejemplos de deficiencias detectadas:
a) El trabajar los cursos con funciones reales con dominios implícitos, crea en estudiantes y profesores la falsa creencia que tanto el dominio como el rango no son parte importante para definir la función y sólo le dan importancia a la regla de asignación (Cuevas et.al, 2005; Cuevas, 2004; Luzín, 1998; Kjeldsen y Petersen, 2014; Blanco et.al., 2014).
b) El visualizar una función como solo una regla de asignación ignorando el dominio y rango conlleva a errores como: no reconocer que valores óptimos de la función fuera del dominio no pueden ser considerados (Moreno y Cuevas, 2004) o que realizar operaciones algebraicas entre funciones puede alterar el dominio.
c) La carencia de recursos para representar el concepto de función en los diversos registros de representación semiótica (RRS) que le son propios. Duval (1993) muestra que mientras algunos estudiantes son capaces de manejar algebraicamente las expresiones de una función lineal o afín, estos mismos se muestran incapaces de reconocer a las mismas en el plano cartesiano y viceversa.
Un breve análisis epistemológico
¿Es de verdad difícil de comprender el concepto matemático de función? Para responder a esta pregunta Artigue (1990) propone que nada mejor que realizar un análisis epistemológico, lo que permitiría al profesor tomar conciencia de la distancia entre el “saber sabio y el saber enseñado”. Esto es, examinar la historia y el desarrollo del concepto a enseñar, para dimensionar su verdadera complejidad.
El origen del concepto de función, según Pedersen (citado por Youschkevitch 1976, 42) se remonta a la civilización babilónica donde se tenía un cierto “instinto de funcionalidad”, que está presente en las tablas de cálculos. Sin embargo, Youschkevitch (1976) afirma que no hay sentido alguno de función en esa matemática, y que el pensamiento matemático de la antigüedad no creó una noción general de cantidad variable o de una función.
En el período medieval latino se hizo alguna contribución interesante de resaltar, pues a partir del siglo XIII aparecieron con regularidad tratados sobre proporciones; trabajos versados sobre relaciones donde n tiene un valor racional. Debe interpretarse que esta teoría de proporciones fue básica en todas las ciencias cuantitativas. Oresme (1320-1382) trataba (con funciones), tasas de cambio que no eran constantes, al generar gráficas constituidas por líneas quebradas o curvilíneas. La latitud de formas representa una larvaria teoría de funciones con la dependencia de una cantidad variable sobre otra. Esto se hizo sin disponer del lenguaje algebraico para expresar la ley de variación o la correspondencia funcional (Boyer 1946, 10; Cuevas y Díaz, 2014).
Gracias a la acumulación de una sucesión de desarrollos matemáticos, entre 1450 y 1650, se fraguó la base para que surgiera el concepto de función, y mostrase un punto de vista dinámico y de naturaleza continua de la relación funcional, en oposición con cualquier visión estática y naturaleza discreta que se quiera reconocer en tiempos anteriores (Kleiner 1989, 283). La palabra función apareció por primera vez en manuscritos de Leibniz Methodus tangentium inversa, seu de functionibus (1673). Con ella, se designaba a un objeto geométrico asociado con una curva. No se utilizaba para designar la relación formal entre la ordenada de un punto de una curva y su abscisa en el sentido moderno. En este sentido debemos reconocer que el cálculo de Newton y Leibniz no fue un cálculo de funciones, sino que fue un conjunto de métodos para resolver problemas de curvas (Kleiner, 1989; Luzín, 1998). No fue hasta 1718 que Johan Bernoulli dio la primera definición formal de función (Youschkevitch 1976, 60): “Por función de una cantidad variable, denotamos aquí una cantidad construida de un modo u otro con esta cantidad variable y constantes”.
La notación fue introducida por Clauriant, y muy utilizada por Euler alrededor del año 1734 (Boyer 1946, 12). Euler fue el primero en darle al concepto de función un papel central y explícito en su obra Introduction in Analysis Infinitorun (Youschkevitch 1976, 61; Luzín, 1998), la define como: “Por función de una cantidad variable denotamos aquí una expresión analítica construida de un modo u otro con esta cantidad variable y números o constantes”.
Esta definición de Euler que consideraba a una función sólo si era continua y se podía escribir mediante una sola formula algebraica, choca con la de d’Alembert; ambos diferían fundamentalmente en el significado que asignaban a la palabra función: d'Alembert entendía por ello cualquier expresión analítica, mientras que Euler entendía por ello cualquier curva dibujada libremente a mano (Luzín 1998, 420). El estudio de los fenómenos físicos obligó a Euler a extender el concepto de función, y es difícil imaginar que tal extensión podría haber sido sugerida por las matemáticas mismas. De hecho, como ha señalado d'Alembert, el formalismo del análisis no tenía mucho sentido para el nuevo tipo de funciones; y al principio, la extensión no agregaba belleza al análisis matemático; por el contrario, forzó su fundamento pero mejoró la aplicabilidad física (Kjeldsen y Lützen 2015, 549).
De donde se genera la primera gran controversia: el desacuerdo entre Euler y d'Alembert es un conflicto clásico entre un rigorista matemático, d'Alembert, y Euler para quien la matemática tuvo que ser moldeada para adaptarse a su uso en la física. De hecho, Euler estuvo de acuerdo con d'Alembert que como se ha tratado hasta ahora, el análisis sólo podía aplicarse a curvas cuya naturaleza puede ser incluida en una ecuación analítica (Kjeldsen y Lützen 2015, 548).
La constante evolución del concepto de función
Los conceptos matemáticos son parte de una estructura lógico-formal que se ha construido con el tiempo y acorde a las necesidades que van surgiendo. Por ello, los conceptos matemáticos evolucionan. Pero esta evolución depende de los problemas a los que se enfrenta la matemática o su aplicación.
Este es el caso del concepto de función, cuando se propone el problema de la cuerda vibrante. El problema consiste en tensar una cuerda entre dos extremos y al hacerla vibrar, encontrar una función que modele la forma de la cuerda en un cierto tiempo t. En esos tiempos se postulaba erróneamente que: Si dos expresiones analíticas coincidían en un intervalo, entonces ellas coincidían dondequiera.
Una
de las propuestas de solución surge con d’Alembert (1749), quien propone la
función como solución a la ecuación de una onda 
.
Esta solución debía tener una expresión analítica dada por una fórmula. Se
trataba de una función impar, periódica y dos veces diferenciable, y esas
deberían ser las únicas soluciones posibles según se creía. Aunque Euler
coincidió con d’Alambert en la ecuación, éste difiere en la interpretación de
la solución (Luzín, 1998; Kjeldsen y Lützen, 2015; Kleiner, 2012).
En
esa misma época surge otra solución al problema de la cuerda vibrante,
propuesta y publicada por Daniel Bernoulli (1755), quien empleando argumentos
físicos y hechos conocidos relativos a las vibraciones musicales propone: 
como
solución. De esta forma, dos respuestas fueron obtenidas para un mismo problema
y, con ello, aparece una contradicción insalvable: Toda función f(x) definida
en el intervalo (0, l) podría ser expresada como la serie:
Tanto Euler como d’Alambert indicaron que esto era absurdo, puesto que implicaría que cualquier función arbitraria tendría que ser impar y periódica. Así entonces, la discusión entre matemáticos se focalizaba sobre el concepto de función y a la conexión entre dependencia funcional y la posibilidad de expresar esta dependencia por medio de una fórmula. Como consecuencia, se estaba obligado a extender la definición de función hacía las funciones definidas por partes. Aunque existían funciones (el valor absoluto) que se podían expresar tanto como fórmula, como por una función por partes (Kjeldsen y Lützen, 2015).
De esta forma, la función se mantiene como una noción mucho más abstracta y universal, que la idea inicial de Euler, por lo que el mismo ofrece una nueva definición en 1755 en su libro Institutiones calculi differentialis donde desaparece el término "expresión analítica":
Sin embargo, si algunas cantidades dependen de otras, de tal modo que, si las últimas se cambian, las primeras también sufren cambios, entonces, las primeras cantidades son llamadas funciones de éstas últimas. Esta es una noción muy amplia y comprende en sí misma a todos los modos a través de los cuales, una cantidad puede ser determinada por otras. Por lo tanto, si x denota una cantidad variable, entonces, todas las cantidades que dependen de x, en cualquier forma que sea o que son determinadas por ella, son llamadas sus funciones (Youschkevitch 1976, 70).
Esta noción de función permaneció prácticamente sin cambio hasta 1797, momento en el que aparece la definición de función dada por Lagrange.
Lagrange (1736-1813) en su tratado Théorie des Fonctions Analytique, restringe la noción de función de Euler, tratando con las actuales funciones analíticas, las cuales están definidas por una serie de potencias positivas en x.
Llamamos función de una o varias cantidades a toda expresión de cálculo, en la cual estas cantidades entran de cualquier manera, mezcladas o no, con otras cantidades que consideramos como valores dados e invariables, mientras que las cantidades de la función pueden recibir todos los valores posibles. Así, en las funciones no consideramos más que las cantidades que suponemos variables, sin ninguna consideración a las constantes que pueden estar mezcladas (Rüting 1984, 73; Luzín 1998, 422).
Esta nueva definición permanece hasta inicios de 1800, Fourier en su trabajo sobre las series trigonométricas encontró relaciones más generales entre las variables (Kjeldsen y Lützen, 2015; Kleiner, 2012) y propuso una evolución para el concepto de función, en su trabajo Analytic Theory of Heat sobre la conducción de calor, que publica en 1822. En la definición de función de Fourier lo principal era la asignación de valores de la función, sin importar si había una o varias fórmulas (Luzín, 1998).
Las imprecisiones alrededor de los conceptos de función y continuidad inquietaban a la comunidad científica-matemática del siglo XIX; y surgen, en esa época, dos nuevas definiciones, la de Cauchy en 1821 en su tratado Analyse Algébrique:
Se llamó a una cantidad variable aquella que se considera tiene sucesivamente varios valores diferentes entre sí. Si las cantidades variables están tan unidas entre sí que, dado el valor de una de ellas, se pueden concluir los valores de todos los demás, se concibe ordinariamente estas diversas cantidades expresadas por medio de una entre ellas, que luego toma el nombre de variable independiente. Y las demás magnitudes expresadas por medio de la variable independiente son las que se llaman funciones de esta variable (Rüting 1984, 74; Youschkevitch 1976, 76).
Como se puede apreciar, esta definición no hace uso de “expresión analítica” y no establece límites en la relación entre las variables que definen a la función, pero no eliminaba la imprecisión del concepto.
La otra definición es la del matemático alemán Dirichlet, quien presenta por primera vez el concepto moderno de una función y = f (x) en un intervalo a < x < b.
Al suponer que a y b son dos valores definidos y x es una cantidad variable que asume gradualmente todos los valores localizados entre a y b. Ahora bien, si a cada x le corresponde un único y finito, de tal manera que, cuando x pasa continuamente por el intervalo de a a b, y = f (x) también varía gradualmente, entonces y se llama una función continua de x para este intervalo. Tampoco es necesario, en absoluto, que y dependa de x en todo este intervalo según la misma ley. De hecho, no es necesario pensar sólo en las relaciones que pueden ser expresadas por las operaciones matemáticas. Representada geométricamente, es decir, al imaginar x e y como la abscisa y la ordenada, una función continua aparece como una curva conectada, para la cual sólo un punto corresponde a cada abscisa entre a y b (Rüting 1984, 74; Youschkevitch 1976, 76).
Luzin (1998) sintetizó la definición de Dirichlet de la siguiente forma:
y es una función de una variable x, definida en el intervalo a < x < b, si a todo valor de la variable x en este intervalo, le corresponde un valor definido de la variable y. Además, es irrelevante en qué forma se establezca esta correspondencia. Luzin (1998, 427)
En esta nueva definición no se restringe a expresar la función por medio de una sola fórmula. Ni siquiera era necesario dar fórmula alguna, puesto que era irrelevante en qué forma se establece la correspondencia.
Esta definición se institucionalizó y permaneció como tal durante varios años y fue considerada por el gremio matemático como la más completa; sin embargo, la última frase “es irrelevante en qué forma se establezca esta correspondencia” empezó a inquietar a la comunidad matemática por imprecisa (Luzin, 1998). Efectivamente, esto causó más debate aún y da origen a la segunda gran controversia.
Conviene recordar que, en esa época, si bien se admitía la naturaleza arbitraria de una función, hasta ese momento, inclusive para Cauchy, las funciones se consideraban explícita o implícitamente como: Producto de expresiones analíticas, o expresiones que podrían representarse gráficamente como curvas. Además, las funciones de interés, eran continuas, diferenciables y como dominio los reales; la célebre función:
(1)
del mismo Dirichlet, echó por tierra esa concepción. Fue tal la confusión que causó esta expresión de función, que en una carta que Hermite dirige a Stieltjes del 20 de mayo de 1893, menciona: Me he alejado, como de cierta llaga, lamentable con miedo y horror de funciones continuas y derivables en ningún punto (Monna 1973, 65).
Cabe advertir, que para que el concepto de función real evolucionara fue necesaria la evolución de otros conceptos involucrados implícitamente, como: variable, número real y conjunto. A finales de 1800, la teoría de conjuntos de Cantor se infiltraba gradualmente en las matemáticas, aunque, era cuestionada y fuente de discusión. Dicha evolución se apoyó en el surgimiento del álgebra simbólica, de la geometría analítica, del cálculo diferencial e integral, y demás. Por su parte los números reales se construían con aportaciones de Cauchy, Bolzano, Weierstrass, y Dedekid, entre otros. Hasta 1900, predominó la idea de que una función debería ser una expresión analítica; así Boole definía función en 1854 como:
Cualquier expresión algebraica envolviendo al símbolo x es llamada una función de x, y puede ser representada bajo la forma abreviada en general como f(x) (Rüting 1984, 75).
Además, prevalecía la no aceptación de las funciones discontinuas y funciones no-derivables como objetos matemáticos. Escritos como La définition en mathématique de Borel, y trabajos en teoría de funciones, estaban encaminados a definir con precisión los objetos matemáticos. En este sentido, Borel afirmaba que:
Cualquier definición en matemáticas debería satisfacer la condición de que, si dos matemáticos dialogaban sobre un objeto matemático, se debería aceptar que ellos se referían al mismo objeto (Monna 1973, 67).
Lebesgue en Sur les fonctions représentables analytiquement de 1905, desarrolla su teoría de la medida y demuestra que existen funciones no representables analíticamente haciendo uso del axioma de Zermelo, de la teoría de cardinales y algunos teoremas de Cantor: “Una función es analíticamente representable o expresable cuando uno puede construirla, siguiendo una ley sobre algunos funcionamientos, esta ley de construcción constituye una expresión analítica” (Lebesgue 1905, citado por Monna 1973, 72).
Para Borel, los métodos no constructivos, como el de Lebesgue, no eran válidos en la matemática: “gran parte del debate fue sobre teoría de funciones. El punto crítico viene a ser cuando una definición de un objeto matemático dado (un número o una función), legitima la existencia de tal objeto” (Kleiner 1989, 296).
Muchos matemáticos siguieron dando nuevos impulsos al continuo desarrollo histórico del concepto de función en un periodo muy fecundo entre finales del siglo XIX y principios del XX. Para Carathéodory (1917), una función es una correspondencia de un conjunto con el conjunto de los números reales (Monna 1973, 82). Bourbaki (1939) en su Théorie des ensembles de 1970, presentó a la función como una regla de correspondencia entre el dominio y el rango, donde ambos conjuntos eran arbitrarios:
Sean
E y F dos conjuntos, los cuales pueden ser o no distintos. A la relación entre
una variable x, elemento de E y una variable y, elemento de F, es llamada una
relación funcional en y si, para toda 
,
existe un único 
el
cual está en la relación dada con x.
Sea considerada una función a la operación con la cual se asocia cada elemento de E con el elemento en F, el cual está en la relación dada con x; y se dice ser el valor de la función para el elemento x, y la función se dice ser determinada por la relación funcional dada. Dos relaciones funcionales equivalentes determinan la misma función (Rüting 1984, 77).
También
Bourbaki definió a la función como un cierto subconjunto del producto
cartesiano de 
;
es decir, la definición de una función como un conjunto de pares ordenados
(Kleiner 1989, 299). El concepto de función matemática se identificó como
correspondencia al concepto de aplicación (mapeo) y con el de transformación
(Martínez, 1993).
Debido a todo lo mencionado, la definición actual de función es la de un objeto sofisticado, consecuencia de numerosas generalizaciones realizadas a través de una evolución de más de 2000 años. Se ha estudiado remplazar la teoría de conjuntos con la teoría de categorías como base fundamental de las matemáticas, y con ello, el concepto de función juega un rol importante.
La teoría de categorías describió una función como una asociación de un objeto A con otro objeto B. Los objetos A y B no necesitan tener elementos (no necesitan ser conjuntos). Una categoría puede definirse como consistente de funciones (aplicaciones), que son tomados como conceptos indefinidos (primitivos) que satisfacen ciertas relaciones o axiomas (Kleiner 1989, 299).
En síntesis, el concepto de función ha tenido una constante evolución en su desarrollo, de tal manera que la definición institucionalizada de la misma ha cambiado en las distintas épocas. Aún más, se considera que el mismo continúa en evolución (Luzín, 1998; Kleiner, 1989).
Este breve análisis epistemológico del concepto de función dimensiona el grado complejidad del concepto y en consecuencia la dificultad que representa la enseñanza y aprendizaje de este concepto, que en principio y como se muestra en las definiciones actuales parecería simple, pero en contraposición su evolución histórica muestra su enorme complejidad.
Se observa, además, que las nociones de relación funcional, expresión algebraica de la función y propiedades como variación, dominio y rango, continuidad, y más tarde número real, sucesiones, conjuntos, cardinalidad y demás, se desarrollaron hasta conformar el concepto de función real actual. También, este análisis permite obtener algunas ideas pedagógicas sobre el pensamiento funcional, que serán de utilidad en el diseño de actividades didácticas, y diferenciar el desarrollo del pensamiento matemático básico desde el punto de vista cognitivo, mediante la definición formal de ambos conceptos.
Metodología
La investigación, propuso una forma de introducir este concepto en el nivel medio superior y superior, mediante el empleo de la tecnología digital que simula fenómenos reales y hace posible incorporar actividades didácticas para desarrollar el pensamiento funcional en donde variación, dominio, variable y rango resulten por demás evidentes para el estudiante Al igual que el pensamiento algebraico facilita la introducción del álgebra, las actividades que promueven el pensamiento funcional facilitaron la adquisición del concepto de función real.
La experiencia se desarrolló con 45 alumnos de nuevo ingreso de la carrera de Ingeniería en Computación (ICO) del Centro Universitario UAEM Valle de Chalco (CUVCH), que cursaron la materia de cálculo diferencial e integral en el semestre 2016B (agosto 2016-enero 2017).
El CUVCH está situado en los suburbios de la Ciudad de México en una zona marginal, donde los estudiantes en su gran mayoría tienen que trabajar y estudiar. El grupo de primer año está constituido por personas provenientes de diversas opciones de bachillerato (técnico y general de la zona), donde sólo el 30% tomó un curso de cálculo previamente. En entrevistas realizadas, se detectó un grupo heterogéneo, ya que se encontraban alumnos que han llevado un estudio continuo desde secundaria, y otros que han dejado de estudiar cierto tiempo y retomaron su preparación profesional.
Las tres actividades se trabajaron con un escenario didáctico interactivo digital (EDID), Polea 1, 2 y 3. El EDID se sitúo en una plataforma y también se distribuyó en CD’s o USB por posibles problemas de conexión a Internet. Para guiar la actividad, cada EDID incluía uno o más cuestionarios que los estudiantes tenían que llenar. Los estudiantes se distribuyeron en duplas por computadora, de modo que uno interactuaba con el EDID y el otro escribía las respuestas, rotando los roles en cada actividad. Al finalizar el llenado de un cuestionario, el profesor los recogía y tomaba uno al azar y mediante una discusión grupal se llegaba al acuerdo de las respuestas correctas. El diseño didáctico de la actividad se basó en la propuesta de Cuevas y Pluvinage (2003).
La clase de cálculo tuvo asignadas cuatro horas por semana: dos en laboratorio tic para el trabajo con los escenarios didácticos y software auxiliar (Derive, CalcVisual), y dos en un salón de clase con implementos usuales (pizarrón y proyector). En la experimentación se asignó un profesor responsable del curso, lo que garantizó la coordinación de todas las actividades.
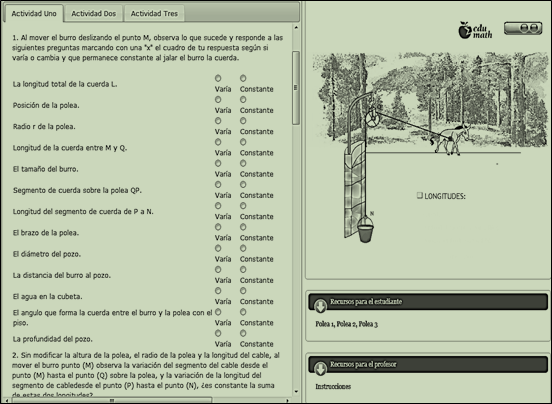
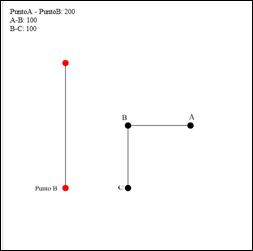
Para introducir el concepto de función el EDID “Polea 1 o introductoria” pretende desarrollar el pensamiento funcional mediante el manejo de una polea simple, y a la vez que el alumno delimite los conceptos de: variación, variable, variable independiente, variable dependiente y parámetro. Una representación de la polea jalada por un burro en un extremo y una cubeta con agua en el otro extremo. Se solicitó al estudiante mover el burro deslizándolo y observar qué sucede. Antes de mover el burro, el estudiante puede modificar: altura de la polea, radio de la polea, y longitud de la cuerda (Figura 1). La primer consulta al estudiante, en el cuestionario, fue sobre variación. Luego se le solicita dejar fijos los valores de altura, radio de la polea y longitud del cable, y se pregunta sobre el valor que cambia en los respectivos segmentos de la cuerda y su relación con la longitud total de la cuerda, a diversos movimientos del burro. Se refuerza al solicitar que observen lo que está fijo y lo que varía, y al cambiar los valores del radio de la polea y la longitud de la cuerda para lograr que el estudiante identifique los conceptos a estudiar: constante, variable independiente, variable dependiente, parámetro, dominio, rango y variación. Para que el estudiante desarrolle las actividades se tienen los RRS: real, gráfico, aritmético y algebraico, que corresponden al Pensamiento aritmético, Pensamiento aritmético avanzado y una aproximación al Pensamiento algebraico.
