___________________________________________

Fecha de recepción del artículo: 30 de mayo de 2017

Fecha de aceptación del artículo: 25 de Septiembre de 2017

DOI: http://dx.doi.org/10.22335/rlct.v9i2.451

* Este artículo es producto del proyecto de Tesis doctoral titulada La relación inversa entre cuadraturas y tangentes en el marco de la teoría de Pirie y Kieren, llevada a cabo en la facultad de Educación de la Universidad de Antioquia (Medellín, Colombia).

** Doctor en Educación. Coordinador de la Línea de Formación en Educación Matemática del Departamento de Educación Avanzada de la Facultad de Educación de la Universidad de Antioquia. Rector Institución Educativa Alfredo Cock Arango-Medellín. Filiación: Docente Universidad de Antioquia. Email: renelondo@gmail.com Contacto: rene2@une.net.co Orcid: http://orcid.org/0000-0003-2073-3474

*** Doctor en Ciencias Matemáticas. Universidad Politécnica de Valencia. Filiación: Docente Universidad de Antioquia. Email: carlos.jaramillo1@udea.edu.co Orcid: http://orcid.org/0000-0002-3937-5032

*** Doctor en Ciencias Matemáticas. Universidad Politécnica de Valencia. Filiación: Docente Universidad EAFIT. Email: pesteban@eafit.edu.co Orcid: http:// orcid.org/0000-0002-5232-1418

Resumen

El presente artículo es un resultado de carácter teórico, derivado de un estudio doctoral en el marco de la línea de Educación Matemática, y tiene como propósito describir similitudes y diferencias relevantes entre el modelo de van-Hiele y la teoría de Pirie y Kieren, los cuales han sido marcos teóricos de algunas experiencias educativas, para la comprensión de conceptos matemáticos en el contexto de la Educación Matemática. Inicialmente, se consideran algunos antecedentes en contexto, para luego comparar las descripciones y la nomenclatura que exhiben los niveles postulados y así caracterizarlos y lograr las conclusiones respectivas. Se trata de poner en escena algunos elementos que permitan argumentar la pertinencia de uno u otro marco teórico, de acuerdo a los propósitos de ciertas investigaciones en el marco de la comprensión de conceptos matemáticos educativa.

Palabras claves: comprensión, niveles, descriptores, caracterización

Abstract

This paper is a result of theoretical character, derived from a doctoral study in the frame of Mathematics Education, and its proposal is to describe important similarities and differences between the model of van-Hiele and Pirie and Kieren theory, and which have been theoretical frameworks of some educational experiences for understanding mathematical concepts. Initially, some backgrounds are considered in context itself, and after to be compared through descriptions and the respective nomenclature that each postulated level exhibits and so for characterizing them in order to achieve the respective conclusions. So, it is about to highlight some elements to argue the relevance of some theoretical framework or another one, according to any research purposes considered within the framework of the understanding of mathematical concepts.

Keywords: understanding, levels, descriptors, characterization

Resumo

Este artigo é resultado do caráter teórico, derivado de um estudo de doutorado no quadro de Educação Matemática, e sua proposta é descrever semelhanças e diferenças importantes entre o modelo de van-Hiele e Pirie e a teoria de Kieren e que têm sido estruturas teóricas de algumas experiências educacionais para a compreensão de conceitos matemáticos. Inicialmente, algumas origens são consideradas em contexto próprio e depois comparadas através de descrições e a respectiva nomenclatura que cada nível postulado exibe e, portanto, para caracterizá-los para alcançar as respectivas conclusões. Então, está prestes a destacar alguns elementos para argumentar a relevância de algum quadro teórico ou outro, de acordo com quaisquer objetivos de pesquisa considerados no âmbito da compreensão de conceitos matemáticos.

Palavras-chave: compreensão, níveis, descritores, caracterização.

Introducción

En el contexto de la educación, los modelos educativos y las teorías para la comprensión son visiones o enfoques pedagógicos que orientan a los especialistas y a los profesores en la elaboración, análisis y sistematización de programas de estudio y estrategias de enseñanza y de aprendizaje, o bien, en la comprensión de algún concepto en particular. Su conocimiento permite a los docentes y, en general, a los investigadores en Educación, concebir las distintas maneras de cómo se elaboran los programas o estrategias, de qué forma se pueden ejecutar y cuáles son los elementos que desempeñan un papel determinante en una planeación o en una intervención didáctica.

Específicamente, en el ámbito de la educación matemática, los modelos educativos y las teorías para la comprensión han constituido históricamente marcos teóricos para el desarrollo de experiencias y estrategias metodológicas, que permiten avanzar en el estudio de la comprensión de conceptos matemáticos, de acuerdo a ciertos estadios o niveles y a unas características validadas en las investigaciones respectivas. Como ejemplos particulares se exhiben, el modelo de van-Hiele y la teoría de Pirie y Kieren; estos marcos teóricos han respaldado en las últimas dos décadas relevantes investigaciones a nivel de programas de maestría y doctorado, y han permitido desarrollar estrategias para la compresión de conceptos matemáticos, entre ellas están: Appropiateness of the van-Hiele model for describing student’s sognitive Processes on algebra task as typified by College students learning of Functions (Land, 1991), Aplicación del modelo de van Hiele al concepto de aproximación local (Llorens Fuster & Pérez Carreras, 1997), La noción de continuidad local desde la óptica de los niveles de van-Hiele (Campillo & Pérez, 1998), Un estudio de la convergencia encuadrado en el modelo educativo de van Hiele y su correspondiente propuesta metodológica (Navarro, 2002), y extensión del modelo de van-Hiele al concepto de área (Prat, 2015); realizadas en universidades como las de Valencia o Sevilla. Otras, consolidadas al interior del Grupo de Investigación Educación Matemática e Historia (UdeA-EAFIT) son: propuesta teórica de entrevista socrática a la luz del modelo de van Hiele (Jaramillo & Campillo, 2001), estudio comparativo del concepto de aproximación local a través del modelo de Van-Hiele (Esteban, 2003), el método socrático y el modelo de van-Hiele (De La Torre, 2003), diseño de una entrevista socrática para la noción de suma de una serie de términos positivos vía área de figuras planas (Jurado & Londoño, 2005), módulo de aprendizaje para la comprensión del conceptos de serie de términos positivos (Zapata & Sucerquia, 2009), relación inversa entre cuadraturas y tangentes en el marco de la teoría de Pirie y Kieren (Londoño, 2011), comprensión de la tasa de variación para una aproximación al concepto de derivada, un análisis desde la teoría de Pirie y Kieren (Villa, 2011); la elipse como lugar geométrico a través de la geometría del doblado de papel en el contexto de van Hiele (Santa, 2011), la comprensión del concepto de continuidad en el marco de la teoría de Pirie y Kieren (Rendón, 2011), relaciones proporcionales entre segmentos en el contexto del modelo de van Hiele (Ibarra, 2014) y la comprensión del concepto de límite de una función en un punto en el marco de la teoría de Pirie y Kieren (Arias & Becerra, 2015). Dado que la teoría de Pirie y Kieren se gesta solo hasta la década de los 80, la lista anterior muestra cómo la misma teoría es objeto de estudio al interior del grupo, a partir del año 2007, actuando como referente para la consolidación de tesis doctoral en 2011.

Las investigaciones anteriores han posibilitado la identificación de puntos de convergencia a nivel metodológico, conceptual y didáctico, pero también, algunos elementos divergentes que han obligado a estudiar con profundidad las características particulares de cada marco teórico y su pertinencia en coherencia con los objetivos que se pretenden alcanzar en los correspondientes estudios.

En esta perspectiva, se hace conveniente realizar un estudio comparativo entre estos dos marcos teóricos para la comprensión, con el fin de describir las principales similitudes y diferencias, y observar en detalle la pertinencia de uno u otro, de acuerdo al tipo de investigación, con la ayuda de algunas experiencias educativas.

Reseña preliminar

Este apartado aborda referentes de cada marco teórico, da cuenta de las teorías que los fundamentan y las experiencias y conceptos que posibilitaron su desarrollo.

En su rol de profesores de secundaria en Holanda, Pierre van Hiele y Dina van Hiele-Geldof, bajo orientaciones de Hans Freudenthal, se interesaron por la manera cómo sus estudiantes se desempeñaban en geometría. Ocurrió que mientras estudiaba algunos de los trabajos de Jean Piaget, Pierre van Hiele formuló su sistema de niveles de pensamiento en geometría. Él notó, como es evidente en algunas de las entrevistas de Piaget, que los problemas o tareas que se presentan a los niños con frecuencia requieren de un conocimiento del vocabulario o propiedades que están fuera del alcance de su nivel de pensamiento. Si la enseñanza acontece en un nivel superior al del estudiante, el material no es asimilado propiamente en la memoria por un periodo largo de tiempo:

En tanto que el niño no sea capaz de reflexionar sobre su propia actividad, el nivel alto se mantiene inaccesible. El nivel alto de operación puede entonces pensarse como un algoritmo, aunque con una consecuencia de poca duración. Esto ha sido probado debido al fracaso en la enseñanza de fracciones. (Freudenthal,1973, p.78).

En 1957, los van Hiele presentaron sus respectivas memorias doctorales en la Universidad de Utrecht, Holanda. Sus disertaciones las acompañaron de experimentos y el desarrollo de una estructura mediante niveles de pensamiento, con el propósito de ayudar a los estudiantes a desarrollar la percepción en la geometría. Pierre van Hiele formuló el esquema y los principios psicológicos y Dina Van Hiele enfocó sus experimentos didácticos con el propósito de elevar los niveles de pensamiento de los estudiantes. Aquí yace el tema del esquema de nivel de van Hiele, que más tarde sería la semilla para extenderlo a conceptos avanzados del análisis matemático, en el estudio llevado a cabo por Llorens (1995).

En la teoría de Pirie y Kieren. La teoría de Pirie y Kieren sobre la evolución de la comprensión surge desde un referente netamente constructivista y está basado en la concepción de comprensión de Glasersfeld (1987), quien propuso la definición “el organismo de la experiencia se convierte en un constructor de estructuras comunicativas” (Glasersfeld, 1987, p. 23) que pretende resolver dichos problemas conforme el organismo los percibe o los concibe…entre los cuales se encuentra el problema interminable de las organizaciones consistentes de dichas estructuras que podemos llamar comprensión. Y añade que la comprensión es un proceso continuo de organización de estructuras de conocimiento de una persona.

El origen inicial de la teoría se fundamenta en la observación y la manera cómo se logra la comprensión de las matemáticas a nivel escolar medio y superior (universitario) en conceptos como las fracciones y las funciones cuadráticas. Pirie y Kieren fundamentan su modelo con experimentos de enseñanza en ambientes constructivistas analizados en intervenciones orales o escritas, mediante entrevistas individuales, grabaciones en video y audio de actividades desarrolladas por estudiantes.

Descripción y caracterización de los marcos teóricos

Se pretende realizar una descripción general de los elementos que componen tanto el modelo de van-Hiele como la teoría de Pirie y Kieren, con el fin de caracterizar ciertos rasgos comparables que puedan dar ideas acerca de la pertinencia de cada uno de ellos.

En el modelo de van-Hiele. El modelo de van Hiele se compone de tres elementos principales: los niveles de van Hiele, son una estratificación del razonamiento humano en una jerarquía de niveles; las fases de aprendizaje, son los procesos que conducen al estudiante desde un nivel de razonamiento al siguiente y la percepción-insight, que es el interés original y el tema de disertación. En la teoría está implícita la idea de que los estudiantes se encuentran con obstáculos en tanto intentan, quizás sin saberlo, el ascenso desde un peldaño al siguiente en la escalera de los van Hiele.

El modelo educativo de van Hiele, tal como se utiliza actualmente, puede enunciarse de la siguiente manera:

· Existen diferentes niveles de razonamiento de los estudiantes referidos a las Matemáticas.

· Cada nivel supone una forma de comprensión, un modo de pensamiento particular, de manera que un estudiante solo puede comprender y razonar sobre los conceptos matemáticos adecuados a su nivel de razonamiento.

· El proceso de enseñanza debe adecuarse al nivel de razonamiento del estudiante. Una enseñanza que transcurra en un nivel superior al de los estudiantes no será comprendida.

· El proceso de enseñanza debe orientarse a facilitar el progreso en el nivel de razonamiento, de forma que el progreso se haga de un modo rápido y eficaz.

Las fases de aprendizaje están orientadas desde un nivel de razonamiento a otro. Van Hiele (1986) describe el paso de un estudiante de un nivel al siguiente como una función de aprendizaje: “la transición de un nivel al siguiente no es un proceso natural, tiene lugar bajo la influencia de un programa de enseñanza-aprendizaje. La transición no es posible sin el aprendizaje de un nuevo lenguaje”. El paso de un nivel al siguiente se produce a través de una específica secuencia de fases de aprendizaje.

Para que una clasificación en niveles pueda considerarse dentro del modelo de van Hiele, es necesario que los indicadores de nivel, llamados descriptores, cumplan con propiedades específicas enunciadas a continuación. Es prudente advertir que la nomenclatura que se utiliza es la presentada por Usiskin (1982):

Propiedad 1: (Secuencialidad fija). Cada estudiante debe progresar a través de los niveles en una secuencialidad fija, esto es, “Un estudiante no puede estar en un nivel n de van Hiele sin haber superado el nivel n-1”

Propiedad 2: (Adyacencia). El objeto de percepción del nivel n-1 se convierte en el objeto de pensamiento del nivel n.

Propiedad 3: (Distinción). El nivel n requiere de una reorganización o reinterpretación del conocimiento adquirido en el nivel n-1, esto es, la percepción de una nueva estructura.

Propiedad 4: (Separación). Dos personas que razonen en diferentes niveles no podrán entenderse, en lo que se refiere al objeto de su razonamiento matemático.

Propiedad 5: (Cada nivel tiene su lenguaje). Hay una estrecha relación entre el lenguaje y los niveles hasta el punto de que cada nivel tiene un tipo de lenguaje específico, de modo que las diferentes capacidades de razonamiento asociadas a cada uno de los niveles de van Hiele, no sólo se reflejan en las formas de resolver problemas, sino que sobre todo, se manifiestan en la forma de expresarse y en el significado que se da o se puede dar al vocabulario específico, como es el caso de la palabra demostrar, por ejemplo. Esta palabra tiene significados típicamente diferentes según el nivel de razonamiento.

Propiedad 6: (Consecución). El progreso de un nivel al siguiente se produce de forma gradual. Algunos investigadores como Hoffer (1983) y Fuys, Geddes, & Tischler (1985), han desglosado cada nivel de van Hiele en varias habilidades de razonamiento, de forma que sólo se puede considerar adquirido un nivel cuando se manifiestan cada una de sus cualidades.

En la teoría de Pirie y Kieren. La teoría de Pirie y Kieren es una propuesta que consiste en el análisis de la gradación de la comprensión de un concepto matemático. El modelo postula ocho niveles que componen su aspecto descriptivo (evolución de la comprensión) y está dotado por unas características identificadas y analizadas por sus creadores. Los ochos niveles describen la evolución de la comprensión matemática en cuanto a conceptos o relaciones entre conceptos.

De otro lado, las características esenciales del modelo son tres: folding back, que es quizás la característica más importante del modelo y tiene que ver con el proceso dinámico de redoblar. En uno de sus artículos, Pirie y Kieren (1989) afirman al respecto “El redoblamiento permite a una persona funcionar en un nivel exterior y enfrentarse con un desafío para regresar a un nivel de comprensión más interno con el fin de reconstruir esa comprensión como base para nuevos niveles externos de comprensión”.

De esta manera, se provoca la reexaminación de la comprensión de un nivel de forma distinta, a partir de las acciones que aparecieron originalmente cuando se trabajó en dicho nivel. La diferencia es cualitativa y realmente distinta debido a la motivación asociada con volver a doblar y la comprensión desarrollada en los anillos externos (Pirie & Kieren, folding back: Dynamics in the growth of mathematical understanding, 1991).

Figura 1. Una representación diagramática del modelo para la evolución de la comprensión matemática, en el cual los límites de falta de necesidad están representados por los aros más gruesos.

La segunda característica importante del modelo tiene que ver con los llamados límites de falta de necesidad que son representados en el siguiente diagrama del modelo. Figura 1.

Estos límites se refieren al progreso del estudiante hacia una comprensión más elaborada y estable, que no requiere necesariamente de los elementos de los niveles más bajos (Pirie y Kieren, 1992). Entonces, si un estudiante se mueve entre límites de falta de necesidad significa un importante cambio cualitativo en la comprensión de la persona. No obstante, es posible que un estudiante regrese a niveles bajos de comprensión, aun cuando hayan sido superados límites de falta de necesidad previamente.

La tercera característica fundamental de la teoría tiene que ver con las complementariedades de la acción y la expresión en los niveles (a excepción del primero y el último). Pirie y Kieren (1994) en su artículo “Growth in mathematical understanding: how can we characterise it and how can we represent it?” afirman:

“El último rasgo de la teoría que aquí, queremos mencionar, es la de la estructura dentro de los mismos niveles. Más allá del primitive knowing cada nivel se compone de una complementariedad de acción y expresión y que cada uno de estos aspectos de la evolución de la comprensión es necesario, antes de moverse desde cualquier nivel”. (Pirie y Kieren, 1994).

Además, el crecimiento ocurre actuando primero y luego expresando, pero con más frecuencia a través de y desde el movimiento entre estos aspectos complementarios. En cualquier nivel, la actuación (el desempeño) abarca toda la comprensión previa, suministrando continuidad con los niveles internos, y la expresión brinda sustancias distintas a ese particular nivel.

Esta característica expresa la importancia de dos aspectos fundamentales, los cuales registran los estudiantes cuando están comprendiendo conceptos matemáticos en situaciones de aprendizaje, y resaltan la importancia de expresar con respuestas procedimientos, quizás no esperados, pero que pueden indicar una actitud innovadora o de descubrimiento de relaciones matemáticas. La respuesta creativa será aquella que aparece como nueva para el sujeto que la produce; puede considerarse como un descubrimiento, en unos casos, o como una invención, en otros. En tal sentido, los estándares básicos de competencias en matemáticas del sistema educativo colombiano están orientados a la conceptualización por parte de los estudiantes, a la comprensión de sus posibilidades y al desarrollo de competencias que les permitan afrontar los retos actuales, incluyendo la adquisición de informaciones y al importar el ejercicio de competencias o formas de actuación que puedan ser nombradas como características del pensamiento matemático en general, y lógico en particular, además de las actitudes de los estudiantes. Términos que sirven para etiquetar las complementariedades de la acción y la expresión para cada nivel llegan a ser primitive knowing, image making, image having, property noticing, formalizing, observing, structuring, investising; acorde a la acción llegan a utilizarse etiquetas image doing, image seeing, porperty predicting, method applying, feature identifying, theorem; y etiquetas de expresión image reviewing, image aying, porperty recording, method justifying, feature prescribing, theorem proving.

Pirie y Kieren también caracterizan las complementariedades de los niveles 2, 3 y 4, haciendo uso de una descripción general, de acuerdo a una experiencia de enseñanza en cuanto a la ecuación cuadrática. En el siguiente cuadro se describen los rasgos generales que dan cuenta del momento en que el aprendiz actúa, expresa, y ejemplifica, de acuerdo a la experiencia de aprendizaje con la ecuación cuadrática. Es importante anotar que Pirie y Kieren hacen esta descripción para los niveles ya mencionados. Los resultados presentados, muestran como aporte la caracterización de las demás complementariedades para los siguientes niveles, de acuerdo a ciertas situaciones de aula

Fuente: Autor

La teoría de Pirie y Kieren considera además, otras características que enriquecen la teoría, y provee a los investigadores de una fundamentación teórica más amplia que permite describir y evaluar con mayor precisión la evolución de la comprensión del aprendiz.

Los niveles externos crecen en forma recursiva desde los niveles internos, pero el conocimiento a un nivel externo permite, y de hecho retiene, los niveles internos. Los niveles externos a su vez, se insertan y envuelven a los internos. Por esto se dice que el modelo es en realidad una teoría de la relatividad de la comprensión.

En este sentido, se puede observar que Pirie y Kieren conciben el conocimiento primitivo, como un generador de modelos completos, similares a la totalidad. Esta propiedad otorga al centro interno la cualidad de carácter fractal. La figura, muestra las complementariedades de la acción y la expresión en cada nivel, de acuerdo al modelo

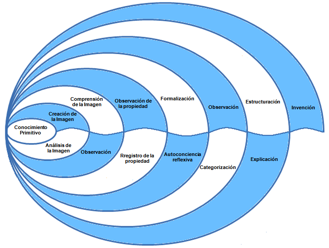
Figura 2. Una representación diagramática de la teoría para las complementariedades de la acción y la expresión, en cada nivel

Esta secuencia o carácter fractal, señala la importancia de la información que se encuentra en el centro interno, toda vez que al recorrer los niveles del modelo hasta llegar al nivel de invención, es susceptible de convertirse en un nuevo conocimiento primitivo para la comprensión de otro conocimiento más elaborado (Pirie & Kieren, 1989).

•El modelo postula la imposibilidad de que un individuo conozca realmente que está sucediendo en la mente de otro individuo (la cual es una postura constructivista radical de Glasersfeld que está en desacuerdo con la postura de Piaget al respecto).

•Cada uno de los niveles delinean un cambio cualitativo en la evolución de la comprensión del estudiante.

•El modelo reconoce la utilidad de las entrevistas con el fin de rastrear los movimientos de los estudiantes a través de los niveles de comprensión. En particular, Pirie y Kieren creen que un instrumento escrito, en especial un examen de opción múltiple, no expone completamente lo comprendido por el estudiante por lo que ésta sólo puede ser inferida y no medida.

•Se da total importancia a las preguntas provocativas, invocativas y de validación.

•Se postula el hecho de que La comprensión matemática de cada persona es única.

Nomenclatura de los marcos teóricos. La estructura de ambos marcos teóricos para analizar el avance en la comprensión de un estudiante en cuanto a un concepto matemático, tiene similitudes en lo que se refiere a la gradación mediante los niveles que ambos contemplan, sin embargo, difieren en la cantidad.

Los van Hiele enunciaron originalmente su modelo, distinguiendo cinco niveles (Básico o nivel 0, y niveles I, II, III y IV). A través de la bibliografía sobre el tema, ellos y otros autores han ido refinando la forma de referirse a estos niveles. El mismo P. van Hiele (1986) en la más notable revisión de su teoría, enfatiza la importancia de los tres primeros niveles, a los que se refiere como: “básico o nivel visual, segundo nivel o nivel descriptivo, tercer nivel o nivel teórico”.

En el mismo trabajo, señalan que los niveles superiores a estos presentan dificultades para su discernimiento y sólo tienen un interés teórico. Sin embargo, la forma más habitual de referirles es distinguir cuatro niveles. Por ejemplo, Gutiérrez & Jaime (1990) etiquetan los niveles así: nivel I (de reconocimiento), nivel II (de análisis), nivel III (de clasificación), nivel IV (de deducción formal). Por su parte, Land (1991) habla de nivel 0 (básico, visual o predescriptivo), nivel I (descriptivo), nivel II (teórico) y nivel III (deductivo). Por último, Llorens Fuster & Pérez Carreras (1997), adicionan a estos cuatro niveles un nivel anterior, que se denomina nivel 0 o predescriptivo.

Nivel 0, predescriptivo

Nivel I, de reconocimiento visual

Nivel II, de análisis

Nivel III, de clasificación, de relación

Nivel IV, deducción formal (Llorens, 1994, p. 84)

En la teoría de Pirie y Kieren, cada uno de los niveles de comprensión puede describirse, de manera tal que se pueda detectar el nivel en que se encuentra un estudiante al razonar en cuanto a un concepto matemático y, a la vez, pueda diseñar estrategias que permitan mejorar la comprensión. Se toma de Meel (2003) la interpretación de los niveles de comprensión del modelo.

•Nivel 1. Conocimiento primitivo. Los estudiantes afloran en su mente toda la información asociada a ideas intuitivas (conocimiento intuitivo) o experiencias de aprendizaje relacionadas con el concepto objeto de estudio, conocimiento situado, en términos de Brown, Collins y Duguid (1989) o conocimiento previo o informal (Saxe,1988).

•Nivel 2. Creación de la imagen. El estudiante es capaz de realizar distinciones con base en capacidades y conocimientos anteriores. Las imágenes no necesariamente son representaciones pictóricas, sino que transmiten el significado de cualquier tipo de imagen mental. Las acciones realizadas en este nivel se relacionan con los aspectos mentales o físicos que se evidencien, con el fin de obtener una idea sobre el concepto objeto de estudio.

•Nivel 3. Comprensión de la imagen. En este nivel, el estudiante se ve en la necesidad de reemplazar las imágenes asociadas a una sola actividad, por imágenes mentales. El desarrollo de tales imágenes mentales que no son más que imágenes orientadas por un proceso, libera al estudiante de las matemáticas a partir de la necesidad de realizar acciones físicas particulares (Pirie y Kieren, 1992). Aquí, el estudiante comienza a reconocer las propiedades globales obvias de las imágenes matemáticas inspeccionadas.

•Nivel 4. Observación de la propiedad. El estudiante examina una imagen mental y determina los distintos atributos asociados con dicha imagen, observa las propiedades internas de una imagen específica además de las distinciones, combinaciones o conexiones entre las distintas imágenes mentales. También construye y modifica definiciones mediante la combinación de tales propiedades. Es posible también que desarrolle un concepto-definición (Tall & Vinner, 1981), creado a partir de la interacción entre las diversas imágenes vinculadas, en lugar de imágenes desconectadas.

•Nivel 5. Formalización. El estudiante conoce las propiedades para abstraer las cualidades comunes de las clases de imágenes, abandona los orígenes de la acción mental, para finalmente producir definiciones matemáticas completas. Es importante anotar que las descripciones generales proporcionadas deben ser equivalentes a una definición matemática adecuada, aun cuando no sea necesario usar un lenguaje matemático formal.

•Nivel 6. Observación. El estudiante utiliza su pensamiento formal, es decir, produce verbalizaciones relacionadas con la cognición sobre el concepto formalizado, es capaz de combinar definiciones, ejemplos, teoremas y demostraciones para identificar componentes esenciales, ideas de conexión y los medios para relacionar dichas ideas.

•Nivel 7. Estructuración. Trasciende a la comprensión, explica interrelaciones de dichas observaciones mediante un sistema axiomático (Pirie & Kieren, 1989).

•Nivel 8. Invención. El estudiante es capaz de liberarse del conocimiento estructurado que representa la comprensión total y crea preguntas totalmente nuevas que tendrán como resultado el desarrollo de un concepto nuevo. En este nivel, la comprensión matemática del estudiante es infinita, imaginativa y llega más allá de la estructura actual, lo que hace que el conocimiento estructurado se convierta en una nueva dimensión de conocimiento dotado con otra estructura quizás isomorfa a la actual, que a su vez se convertirá en un nivel de conocimiento primitivo. La tabla 2, muestra características de cada marco teórico fundamentadas en los elementos comunes y disímiles que se pudieron encontrar, con el fin de poder establecer un resumen comparativo:

Tabla 3. Resumen comparativo entre los dos marcos teóricos

Métodología

Dado que el estudio se enmarca en el campo de la educación matemática, se ha elegido precisamente el enfoque cualitativo como el más pertinente para el contexto del estudio, teniendo en cuenta que los métodos de recolección de datos utilizados son no estandarizados y se llega a perspectivas más generales, construyendo la hipótesis que se va refinando conforme se recaban los datos La investigación tiene un alcance explicativo (Cazau, 2006), en un intento por identificar algunas categorías mostradas en la tabla anterior, las cuales se constituyen en variables relacionadas o disímiles, teniendo como criterio los elementos que pueden ser contrastados entre uno y otro marco teórico, siendo la identidad de clase lo que legitima la comparación entre aspectos del mismo género o especie.

Fuente: Autor

Resultados

El estudio no pretende determinar cuál de los dos marcos es el mejor, más si proporcionar a los investigadores que estudian la comprensión matemática, criterios que permitan argumentar la conveniencia del marco teórico a utilizar, en correspondencia con el estudio que se desea llevar a cabo, de acuerdo a elementos que tienen que ver con las teorías gestantes, las características que postulan, la gradación y los elementos que componen los niveles y las investigaciones que han sido realizadas desde cada uno de los marcos teóricos. En este sentido, el modelo de van Hiele se destaca por ser más pertinente en estudios que tengan por objeto describir la comprensión de conceptos geométricos y del Análisis Matemático, de manera secuencial y en la que el lenguaje se convierte en un descriptor determinante para la caracterización del nivel de razonamiento; por su parte, la Teoría de Pirie y Kieren se convierte en un soporte teórico apropiado para estudios en los que el análisis de los retrocesos (Folding back) y avances en el razonamiento, la exploración de las actuaciones y las declaraciones de los participantes (complementariedades de la actuación y la expresión) se convierten en factores determinantes para dilucidar posibles momentos de comprensión.

Discusión y Conclusiones

El presente estudio de carácter teórico compara similitudes y diferencias entre el modelo de van-Hiele y la teoría de Pirie y Kieren y es producto de una tesis doctoral en el campo de la Educación Matemática del programa de Doctorado en Educación de la Universidad de Antioquia. Este extracto teórico permite reconocer elementos convergentes y divergentes entre ambos marcos teóricos para la comprensión de conceptos matemáticos, con el fin de posibilitar futuros estudios en esta línea.

Así las cosas, como elementos convergentes, se tiene que ambos marcos teóricos se gestan desde referentes constructivistas que se fundamentan en teorías para la comprensión de conceptos matemáticos, postulando una gradación de la comprensión acorde con unas características generales inicialmente y, luego, particulares, en el contexto de cada investigación, lo que en los últimos años se ha consolidado como los descriptores propios para la comprensión de cada concepto. Se enfatiza también en la importancia que tiene el lenguaje en ambos marcos teóricos como elemento determinante en el avance de los niveles, en pos del refinamiento que el estudiante va mostrando a través de una entrevista o cualquier otra intervención, desde el modelo de van-Hiele como característica plausible en el desarrollo de su teoría y, desde la teoría de Pirie y Kieren en sus complementariedades de la expresión que postula.

Finalmente, se logra dilucidar como elemento divergente a destacar, que en el modelo de van-Hiele algunas de las características consideradas como la de secuencialidad fija y la de adyacencia son particularmente más lineales y no precisamente más cercanas al fenómeno de comprender, que la característica del Folding back presentada en la teoría de Pirie y Kieren, la cual permite una retrospección y reacomodación de los procesos de comprensión que no han funcionado bien en niveles más internos; de hecho, esta última característica es determinante para detectar un avance en la comprensión del concepto particular.

Referencias bibliográficas

Arias, J., & Becerra, M. (2015). La comprensión del concepto de límite de una función en un punto en el marco de la teoría de Pirie y Kieren. Antioquia: Universidad de Antioquia

Brown, J., Collins, A., & Duguid, P. (1989). Situated cognitionand the culture of learning. Educational Researcher, 18(1), 32-42.

Campillo, P., & Pérez, P. (1998). La noción de continuidad desde la óptica de los niveles de van-Hiele. Divulgaciones Matemáticas, 6(1), 69-80.

Cazau, P. (2006). Introducción a la Investigación en Ciencias Sociales (3 ed.). Buenos Aires, Argentina: Unex.

De La Torre, A. (2003). El método socrático y el modelo de van-Hiele. Lecturas Matemáticas, 24, 99-121.

Esteban, P. (2003). Estudio comparativo del concepto de aproximación local a través del modelo de van Hiele. Valencia. 2003. Tesis doctoral publicada. Valencia, España: Universidad Politécnica de Valencia.

Freudenthal. (1973). Mathematics as an Educational Task. Dordreckt, Holland: Reidel Pub.Co.

Fuys, D., Geddes, D., & Tischler, R. (1985). An investigation of the van Hiele model thinking in geometry among adolescents (final report). Nueva York: Brooklyn College.

Glasersfeld, E. (1987). The Construction of Knowledge. Seaside: Intersystems Publications.

Gutiérrez, Á., & Jaime, A. (1990). Una propuesta de fundamentación para la enseñanza de la geometría: el modelo de van Hiele. En L. y. Sánchez, Teoría y práctica en Educación Matemática. Sevilla: Alfar.

Hoffer, A. (1983). Van Hiele-Based Research. Acquisition of mathematical Concepts and processes. Nueva York: Brooklyn College.

Ibarra, T. (2014). Relaciones proporcionales entre segmentos en el contexto del modelo de van Hiele. Antioquia: Universidad

Jaramillo, C., & Campillo, P. (2001). Propuesta teórica de entrevista socrática a la luz del modelo de van-Hiele. Divulgaciones matemáticas, 9(1), 65-84.

Jurado, F., & Londoño, R. (2005). Diseño de una entrevista socrática para la noción de suma de una serie de términos positivos vía área de figuras planas. Antioquia: Universidad.

Land, J. (1991). Appropriateness of the van Hiele Model for Describing Students´ Cognitive Processes on Algebra Tasks as Typified by College Students´ Learning of Functions. Boston: University of Boston.

Llorens Fuster, J. L., & Pérez Carreras, P. (1997). An extension of van Hiele´s model to the study of local approximation. Int. J. Math. Edu. Sci. Technol., 28(5), 713-726.

Llorens, J. (1995). Extensión del modelo de van Hiele a un ámbito diferente de la geometría en niveles educativos elementales. Valencia, España.

Londoño, R. (2011). La relación inversa entre cuadraturas y tangentes, en el marco de la teoría de Pirie y Kieren. Tesis Doctoral, Universidad de Antioquia. Antioquia: Universidad

Meel, D. (2003). Models and theories of Mathematical Understanding: Comparing Pirie and Kieren’s Model of the Growth of Mathematical Understanding and APOE theory. CBMS Issues in Mathematics Education, 12, 132-181.

Navarro, A. (2002). Un estudio de la convergencia, encuadrada en el modelo de van-Hiele, y su correspondiente propuesta metodológica. Sevilla: Alfar.

Pirie, S., & Kieren, T. (1989). A recursive theory of mathematical understanding. For the Learning of Mathematics, 9(3), 7-11.

Pirie, S., & Kieren, T. (1991). folding back: Dynamics in the growth of mathematical understanding. Fifteenth Meeting of the Psychology of Mathematics Education Conference. Assissi, Italy.

Pirie, S., & Kieren, T. (1991a). A dynamic theory of mathematical understanding: Some features and implications. (E. D. Service, Ed.) (ED 347 067).

Pirie, S., & Kieren, T. (1992). Creating constructivist environments and constructing creative mathematics. Educational Studies in Mathematics, 0, 505-528.

Pirie, S., & Kieren, T. (1994). Growth in mathematical understanding: How can we characterise it and how can we represent it? Educational Studies in Mathematics, 26(2-3), 165-190.

Prat, M. (Diciembre de 2015). Extensión del modelo devan Hiele al concepto de área. España: Valencia.

Rendón, R. (2011). La comprensión del concepto de continuidad en el marco de la teoría de Pirie y Kieren. Antioquia: Universidad.

Santa, Z. (2011). La elipse como lugar geométrico a través de la geometría del doblado de papel en el contexto de van Hiele. Antioquia: Universidad de Antioquia.

Saxe, G. (1988). Studying working intelligence. En B. Rogoff, & J. Lave, Everyday cognition (págs. 9-40). Cambridge.

Tall, D., & Vinner, S. (1981). Conceot image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151-169.

Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with special reference to limits and continuity. Educational Studies in Mathematics, 12, 151-169.

Usiskin, Z. (1982). van Hiele Levels and Achievements in Secondary School Geometry. CRRSSG Report, Universidad de Chicago.

Van Hiele, P. (1986). Structure and Insight: A Theory of Mathematics Education. New York: Academic Press.

Van Hiele, P. (1986). Structure and insight: A Theory of Mathematics Education. New York: Academic Press.

Villa, J. (2011). La comprensión de la tasa de variación para una aproximación al concepto de derivada, un análisis desde la teoría de Pirie y Kieren. Antioquia: Universidad.

Yin, R. (2009). Case study research, Design and methods. California: Sage Publications, Inc.

Zapata, s., & Sucerquia, E. (2009). Módulo de aprendizaje para la comprensión del conceptos de serie de términos positivos. Antioquia: Universidad

Zapata, S., & Sucerquia, E. (2009). Módulo de aprendizaje para la comprensión del concepto de serie de términos positivos. Antioquia: Universidad.

Nivel		Acción	Expresión
Image making	Image doing. Construcción de imagen mental o física del concepto matemático (tablas, puntos). Sigue instrucciones dadas por el profesor sin ningún tipo de análisis. No examina los resultados. No ha pasado al image reviewing cuando simplemente ve su acción previa completada y de cierta manera rechaza regresar a ella por algo menos que lo limite a una regla. Ejemplo: Formación de una imagen para la gráfica de una ecuación cuadrática. Juntar los puntos (tabla de valores) en el orden en el que fueron calculados		Image reviewing. Consideración de la imagen como un todo. Se da importancia al orden en el que se ejecutan las instrucciones. Hay análisis del trabajo realizado por las instrucciones dadas y adaptan nuevas tareas a ciertas ideas tentativas de cómo las imágenes deben ser construidas. No ha pasado al image doing cuando permite la alteración del comportamiento previo, todavía no visualiza un patrón propio del concepto. Ejemplo: Consideración de una gráfica como un todo antes de desplazarse a la otra (de construir la otra), ver cierto patrón dentro de la actividad de graficación. Análisis descriptivo del trabajo realizado.
Image having	Ubican puntos en la gráfica siguiendo la instrucción correspondiente, pero no se cercioran si éste pertenece a la gráfica Identifica un elemento discrepante, por ejemplo, un punto que al ubicarlo, no corresponde a la gráfica de una función cuadrática. El estudiante lanza declaraciones después de haber graficado varias funciones como: "eso no puede ser correcto", "ese punto no puede ir allí".		Image saying. Explicación del por qué un elemento discrepante no se acomoda a su imagen. Articula las características del patrón identificado. Está en posición de hablar acerca de sus acciones y llevarlas más allá de la acción de graficar. Ejemplo: Lanza expresiones como: "Yo pensé que todos ellos formaban una U", "hemos conseguido ya un punto para x=2", "todos los que están en el fondo de la U son puntiagudos". No necesariamente implica tener la gráfica correcta o completa.

Nivel		Acción	Expresión
Observing	Feature identifying Utiliza como referencia su pensamiento formal. El estudiante observa la estructura general del concepto con el fin de estructurar y organizar sus procesos de pensamiento, así como también, reconocer las ramificaciones de los procesos de pensamiento. El estudiante combina las definiciones, ejemplos, teoremas y demostraciones que circundan el concepto particular para identificar los componentes esenciales, las ideas de conexión y los medios para cruzar entre dichas ideas. Ejemplo: En las gráficas realizadas por él, intenta ubicar el punto fijo y la recta fija que identifica como elementos comunes en todas las parábolas. Haciendo uso de las palabras: foco, directriz, distancia focal; se hace una idea de la definición.		Feature prescribing Produce verbalizaciones relacionadas con la cognición, sobre el concepto formalizado, de acuerdo a las propiedades que describió en el nivel anterior. Dicho de otra manera, el estudiante hace uso de la meta-cognición (ya que tiene un nivel mucho mayor de abstracción) para enunciar la definición del concepto particular, haciendo uso de un lenguaje matemático formal. Ejemplo: El estudiante es capaz de definir la parábola en sus propias palabras, de manera equivalente, como "el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz". Deduce, de acuerdo a las características abstraídas, las aplicaciones que una parábola tiene en la vida práctica.
Structuring	Theorem conjecturing. Interpreta la interrelación de las observaciones hechas mediante un sistema axiomático. Hace uso de otros ejemplos con el fin de validar sus creencias o conjeturas, relacionando ideas subyacentes, axiomas y otras definiciones, a través de otros dominios. Percibe de manera coherente la interconexión de diversas teorías, hasta llegar a un teorema. Ejemplo: El estudiante descubre, después de varios intentos, que en todas las parábolas con vértice en el origen, existe una directriz y un foco, tales que los puntos de la parábola equidistan de estos elementos. Relaciona ejemplos, teoremas y definiciones para llegar a su conclusión.		Theorem proving.. Es capaz de demostrar el teorema establecido de manera verbal o en forma escrita, haciendo uso del lenguaje matemático adecuado. Ejemplo: El estudiante, es capaz de deducir la ecuación general de la parábola, dados algunos elementos. Expresa un resultado y es capaz de establecer si es un teorema.

Marco Teórico Categorías	Modelo de van-Hiele	Teoría de Pirie y Kieren
Creadores	Pierre van Hiele y Dina van Hiele-Geldof.	Susan Pirie y Thomas Kieren.
Teorías gestantes	La teoría del aprendizaje de Jean Piaget	Surge desde un referente netamente constructivista y está basado en la concepción de comprensión de Glasersfeld (1987)
Características que se postulan en el proceso de comprensión	Elementos: Niveles Fases de aprendizaje Percepción-insight Propiedades de los niveles: Secuencialidad fija Adyacencia Distinción Separación Lenguaje Consecución	Folding back Complementariedades de la acción y la expresión Límites de falta de necesidad
Gradación de la comprensión (niveles)	Propone 5 niveles	Propone 8 niveles
Algunas investigaciones realizadas en los últimos años	(Llorens, 1995), (Llorens Fuster & Pérez Carreras, 1997), (Campillo & Pérez, 1998), (Navarro, 2002) (Jaramillo & Campillo, 2001), (De La Torre, 2003) (Esteban, 2003), (Jurado & Londoño, 2005), (Zapata & Sucerquia, 2009), (Santa, 2011), (Ibarra, 2014) y (Prat, 2015)	(Londoño, 2011), (Villa, 2011), (Rendón, 2011) y (Arias & Becerra, 2015)