Concepciones de
los profesores sobre la resolución de problemas en cálculo diferencial e
integral: estudio etnográfico*
Conceptions
of teachers on the resolution of problems for the teaching of concepts of
differential and integral calculus: ethnographic study *
Concepções
dos professores sobre a resolução de problemas no cálculo diferencial e
integral: estudo etnográfico *
Cristhian López Leyton **
Eliécer Aldana Bermúdez ***
Jhon Darwin Erazo Hurtado ****
Universidad del Quindío, Colombia
Fecha
de recepción del artículo: 25 de Agosto de 2017
Fecha de aceptación del artículo: 21 de Diciembre de 2017
DOI: http://dx.doi.org/10.22335/rlct.v10i1.448
*El
artículo es inscribe como resultado del trabajo de investigación titulado “concepciones
de los profesores del programa de licenciatura en matemáticas de la universidad
del Quindío sobre la resolución de problemas en cálculo diferencial e integral:
un estudio etnográfico”.
** Licenciado
en Matemáticas. Filiación: Universidad del Quindío. Correo electrónico: leyton3991@gmail.com.
Orcid: https://orcid.org/0000-0001-7335-2339
***Doctor
en educación Matemática. Filiación: Universidad del Quindío. Correo
electrónico: eliecerab@uniquindio.edu.co. Orcid: https://orcid.org/0000-0003-1691-2699
**** MSc
en Ciencias de la educación. Filiación: Universidad del Quindío. Correo
electrónico: jderazo@uniquindio.edu.co Orcid: https://orcid.org/0000-0002-0036-4264
Universidad Javeriana
Cali. Correo electrónico: gportillaw@gmail.com
Orcid: https://orcid.org/0000-0002-3243-7659
Resumen
Este estudio tiene como
finalidad analizar las Creencias y Concepciones de Profesores sobre la
Resolución de Problemas (RP) para la enseñanza y el aprendizaje del Cálculo
diferencial e integral, en la formación de profesores de matemáticas. Las
creencias y concepciones de profesores universitarios de matemáticas, se
analizan como organizadores que incluyen imágenes mentales materializadas en el
desarrollo de sus clases y las percepciones sobre su práctica educativa. El
enfoque es cualitativo interpretativo y el método utilizado la etnografía, mediante
un estudio de caso. Los resultados permiten concluir que las concepciones que
tienen los profesores sobre RP obedece a un modelo de enseñanza.
Palabras clave: creencia,
concepción, resolución de problemas, cálculo.
Abstract
This
study aims to analyze the beliefs and conceptions of teachers about the problem
resolution (PR) for teaching and learning of differential and integral calculus
in the training of mathematics teachers. The beliefs are conceptions of university
mathematics teachers are organizers that include mental images materialized in
the development of their classes and perceptions about their educational
practice. The approach is qualitative interpretive and the method used by
ethnography, through a case study. The results allow us to conclude that the
teachers' conceptions of PR are due to a teaching model.
Key
words: Belief, Conception, Problem Resolution, Calculus.
Resumo
O objetivo deste estudo é
analisar as Crenças e as Concepções de Professores sobre Resolução de Problemas
(RP) para o ensino e aprendizagem de cálculo diferencial e integral, na
formação de professores de matemática. Para isso, referem-se que afirmam que as
crenças e concepções de professores universitários de matemática são organizadores
que incluem imagens mentais materializadas no desenvolvimento de suas aulas e
as percepções sobre sua prática educacional. A abordagem é qualitativa
interpretativa, e o método utilizado na etnografia, através de um estudo de
caso. Os resultados permitem concluir que as concepções que os professores têm
sobre RP obedecem a um modelo de ensino.
Palavras-chave: Crença,
Concepção, Solução de problemas, Cálculo.
Introducción
La educación matemática
pone a disposición estudiar desde las nociones más básicas hasta las
matemáticas que se enseñan y se aprenden en la educación superior, a partir de
sus rasgos epistémicos, didácticos, cognitivos, todos ellos tendientes a la
preparación de un ciudadano competente para resolver los problemas que emergen
de sus prácticas profesionales. Muchos planes de estudio a nivel de la
educación superior, plantean la resolución de problemas (RP) como eje
articulador transversal y como estrategia para el aprendizaje de los ejes
conceptuales que contempla el proyecto curricular del programa (PEP, 2010).
En este sentido, los
profesores en su proceso de planificación y diseño de clase, realizan procesos
de transposición didáctica (Chevallard, 1991) que implica la preparación del
profesor de un corpus del conocimiento y que pone en juego del saber matemático
(surge de la investigación) al saber enseñando (la práctica en el aula) de
elementos matemáticos que configuran el cálculo. Esta transposición didáctica
emerge de saberes institucionales y personales (Godino, Batanero, Rivas, y
Arteaga, 2013) que cada profesor asocia a una creencia o concepción de como
utiliza la RP como contenido, aplicación después de terminar un tema o unidad
didáctica, o como estrategia de enseñanza aprendizaje, y como proceso ligado al
uso sentido y significado de los objetos matemáticos del conocimiento desde
posturas sociales y culturales que ponen los saberes matemáticos en la dinámica
de las actividades humanas. En este sentido, la RP como estrategia para la
enseñanza de los conceptos fundamentales del cálculo diferencial (CD) y
cálculo integral (CI), está asociada a creencias o intuiciones y a
concepciones o saber personal de los profesores, vinculadas a prácticas
institucionales, personales, epistemológicas, didácticas, instruccionales y
cognitivas, desligadas de contextos reales, lo que hace necesario ser objeto de
estudio (Serrano, 2010).
De acuerdo con el
encuadre epistemológico entre la experiencia personal y búsqueda de literatura
en posturas, políticas nacionales de calidad para la educación superior y las
buenas prácticas de docencia e investigación, se aseveró la necesidad de
analizar desde una postura investigativa el planteamiento ¿Cuáles son las
creencias y las concepciones que tienen los profesores universitarios sobre el
papel de la resolución de problemas en la enseñanza y aprendizaje de los
conceptos fundamentales del Cálculo diferencial e integral?
Aspectos conceptuales
Las creencias están
asociadas a rasgos de tipo subjetivo de las personas, en este caso particular
de los profesores de matemáticas, ligadas a los sentimientos y un poco guiadas
por las emociones relacionadas con aspectos propios de la personalidad; las
creencias obedecen a acciones más de tipo empírico sobre percepciones del
hacer del profesor sobre su práctica pedagógica. Por su parte, (Pajares, 1992)
citado en Gil Cuadra y Rico (2003), considera que las creencias son “verdades
personales indiscutibles, sustentadas por cada uno, derivadas de la experiencia
o de la fantasía, que tiene un fuerte componente evaluativo y afectivo. Las
creencias se manifiestan a través de declaraciones verbales o de acciones
(justificándolas) (Martínez, Vergel, Zafra, 2015).
Asimismo Thompson (1992),
plantea que los docentes difieren ampliamente en sus creencias sobre la
naturaleza y el sentido de las matemáticas, dando al investigador una idea muy
amplia de lo que pueden ser las finalidades más relevantes que puede considerar
el profesor a la hora de plantear y llevar a cabo su cronograma de actividades,
su percepción frente al papel que se juega cada día en su práctica profesional,
cómo se desenvuelve en ella, y el lugar que ocupan sus estudiantes en relación
al entorno matemático. Igualmente se asocian factores importantes a las
creencias como el elemento cognitivo derivado del grado de razonamiento que el
profesor da a sus ideas, un componente afectivo basado en sus experiencias o
circunstancias enfrentadas, y finalmente, elementos conductuales que relacionan
su círculo social y laboral ante sus posiciones en torno a la enseñanza
(Pajares, 1992).
Por otra parte para
García et al. (2006) las creencias por parte del profesor: Son ideas poco
elaboradas, generales o específicas, las cuales forman parte del conocimiento
que posee el docente pero carecen de rigor para mantenerlas- e influyen de
manera directa en su desempeño. Las creencias sirven como filtro para todo
aquello que supone el proceso enseñanza-aprendizaje. (García et al., 2006).
Las concepciones:
incluyen las creencias y en este caso se podría estar hablando de concepciones
de tipo subjetivo, estas obedecen más a procesos mentales construidos y
establecidos que pueden ser además epistemológicos porque obedecen a un conocimiento
sobre el programa o la naturaleza de la enseñanza de las matemáticas. Al
respecto, las concepciones para algunos autores son “organizadores implícitos
de los conceptos, de naturaleza esencialmente cognitiva y que incluyen
creencias, significados, conceptos, proposiciones, reglas, imágenes mentales,
preferencias, entre otras, que influyen en lo que se percibe y en los procesos
de razonamiento que se realizan” (Moreno y Azcárate, 2003, p. 267).
En su estudio Flores
(1998) relaciona el término “concepciones” en torno a las matemáticas de la
siguiente manera; la forma como se concibe el conocimiento y su relevancia
personal (concepciones sobre las matemáticas), método de aprendizaje y
enseñanza (concepciones sobre el estudio y preparación en matemáticas),
aplicabilidad cotidiana (concepciones sobre la adaptabilidad a las situaciones
en contexto), y finalmente su propia preparación para profesor (concepciones
sobre la didáctica de las matemáticas). En este sentido, todos los constructos
que implícitamente la palabra concepción refiere:
"Una
concepción del profesor sobre la naturaleza de las matemáticas puede verse como
creencia, concepto, significado, regla, imagen mental y preferencia, consciente
o inconsciente del profesor en relación a las matemáticas. Éstas creencias,
conceptos, puntos de vista y preferencias, constituyen los rudimentos de una
filosofía de las matemáticas" (Thompson, 1992; p. 132)
Para Porlán (1992) la
palabra concepción ligada al pensamiento del profesor y la formación de
profesores, constituye un sistema para la toma de decisiones acerca de su
praxis, que interviene desde los saberes disciplinares y saberes derivados de
la experiencia y junto a teorías y estrategias aplicadas en las prácticas
profesionales conforman la identidad del docente. Las concepciones se presentan
como un condensado de posturas que un profesor antepone para realizar su
intervención en el aula, es así como estas actitudes referentes a la enseñanza
y aprendizaje conforman la estructura sus estrategias como docente (Contreras y
Carrillo, 1995).
Relación entre creencias
y concepciones: Entre las creencias y las concepciones existe una relación que
podría llamarse de inclusión, al respecto Llinares (1991) reconoce que entre
conocimiento, creencias y concepciones existen diferencias sutiles. Las
creencias son el "contexto psicológico" en el que se produce el
aprendizaje en los cursos de formación; las concepciones constituyen sistemas
cognitivos interrelacionados de creencias y conocimientos que influyen en lo
que se percibe y en los procesos de razonamiento que se realizan. Los
profesores durante sus prácticas generan ideas de cómo desarrollar los
contenidos de la enseñanza, pero sobre todo cómo enseñar a resolver problemas
matemáticos, para ello, utilizan sus ideas producto de la experiencia, pero sin
dejar de lado sus creencias y las concepciones matemáticas. A partir de estas
concepciones el profesor hace la transposición didáctica y utiliza la
resolución de problemas desde diferentes enfoques como: metodología, estrategia,
contenido o aplicación después de concluir la enseñanza de un objeto
matemático.
Las concepciones y
creencias, de acuerdo con Ponte (1994) conciben parte del conocimiento, y en
este sentido, las creencias son certezas descendientes de vivencias o inventiva
propia, muy a diferencia de las concepciones, siendo estas la moldura
organizacional de conceptos involucrados en procesos de cognición que
intervienen al momento de realizar una actividad de cualquier naturaleza.
La resolución de
problemas (RP). La educación matemática ha tenido como fin primordial que los
estudiantes aprendan las matemáticas a partir de la resolución de problemas,
las reformas educativas a través de los estándares por competencias ponen como
telón de fondo la resolución de problemas para que un estudiante logre ser
matemáticamente competente. Efectivamente, gran parte de las investigaciones en
educación matemática llevadas a cabo en diferentes partes del mundo, tienen que
ver con la resolución de problemas como estrategia para el aprendizaje de las
matemáticas.
En este sentido, según
Stanic y Kilpatrick (1989), afirman que los problemas han ocupado un lugar
central en el currículo matemático escolar desde la antigüedad, pero la
resolución de problemas, no. Quienes enseñan matemáticas han aceptado la idea
que el desarrollo de la habilidad para resolver problemas merece una atención.
Junto con este énfasis en la resolución de problemas, sobrevino la confusión.
El término “resolución de problemas” se ha convertido en slogan que acompañó
concepciones sobre qué es la educación, qué es la escuela, qué es la matemática
y por qué debemos enseñar matemáticas en general y resolución de problemas. La
resolución de problemas ha adoptado diferentes significados:
Resolver problemas como
contexto para: enseñar matemática, crear motivación por algunos temas, recrear,
desarrollar habilidades, y práctica. Resolver problemas como habilidad:
rutinarios (habilidades básicas), no rutinarios (de nivel superior), y técnicas
de resolución como contenido para aplicar lo aprendido. Resolver problemas es
“hacer matemática”: creer que el trabajo de los matemáticos es resolver
problemas y que la matemática consiste en problemas y soluciones (Pólya, 1954).
Las concepciones que
poseen los profesores para la RP, la enseñanza y aprendizaje de las
matemáticas, pueden estar ligadas a los mismos significados. Así mismo, estas
concepciones pueden jugar un papel fundamental a la hora de cómo se tiene
interiorizados los conceptos de ejercicio, problema en matemáticas, y
situaciones problema. En síntesis, la matriz representa un paralelo entre lo
que diferentes autores comprenden sobre “ejercicio”, “problema” y “situación problema”
Tabla 1. Paralelo entre
“Ejercicio”, “Problema” y “Situación problema”
|
Ejercicio
|
Problema
|
Situación problema
|
|
Actividad de enunciado claro y concreto que evoca sistemática y
mecánicamente el empleo de un algoritmo o concepto.
Herramienta que procura resolver, evocar o rememorar un objeto
matemático en específico, definición o teorema (Blanco, 1993)
Posee la característica de ser solucionado por una serie de
pasos memorísticos dados (algoritmos), y que en repetidas ocasiones convergen
a procesos netamente numéricos.
En su
práctica la posibilidad de desarrollar habilidades de razonamiento y
competencias para la resolución de problemas son muy limitadas. Schoenfeld
(citado en Blanco, 1993)
Son
utilizados inmediatamente de la exposición del teorema, definición, u objeto
matemático. Esto da la seguridad al estudiante sobre la herramienta que debe
utilizar.
|
Situaciones
formuladas en contexto cuya resolución requiere una traducción del enunciado,
oral o escrito, a expresión matemática (Blanco,1993), ejecutar un plan y
examinar resultados.
Situación
en la que el estudiante propende realizar un proceso para llegar a una meta,
pero no conoce la maniobra que debe realizar para lograrla)
Vínculo
entre el individuo y la tarea; se emplea la palabra problema para describir
una tarea que resulta compleja para el individuo que está tratando de
resolverla (Schoenfeld , 1985)
Su
consecución depende en gran medida de los conocimientos previos y el grado de
compromiso del individuo que lo afronta” (López y Contreras, 2014. p. 426) para
lo cual se hacen necesarias estrategias heurísticas y meta-cognitivas
Circunstancia
que evoca un grado de inseguridad y que ocasiona tácticas orientadas en el
seguimiento de una solución. (Pino, 2012)
|
“problemas
sobre situaciones reales” que representen para el estudiante un contexto
verdadero y significativo en su cotidianidad. El escenario resulta relevante
para la comprensión y la resolución matemática del problema.
Actividades
lo más cercanas posibles a situaciones reales que requieran el uso de
habilidades, conceptos y procesos matemáticos haciendo necesaria para su
solución investigar otros datos relevantes asociados.
“La
solución de este tipo de problemas conlleva a la construcción de un modelo
matemático. El punto de partida en la construcción de un modelo matemático es
un problema real” (Benítez y Londoño, 2009)
Sitúan
a los estudiantes en la esencia de los modelos, instrumentos y operaciones
base de las matemáticas, plasmadas a situaciones concretas del contexto
estudiantil y cotidiano
Se
hace necesario de un suceso, el entorno del problema que aporta datos
relevantes, actores participantes, incógnitas, y finalmente un interrogante
que precisa de una decisión o rumbo.
|
Fuente: Autores
Concepciones de los profesores
sobre la resolución de problemas
Los profesores
universitarios en su proceso de transposición didáctica generalmente apoyan su
práctica pedagógica de manera experimental en modelos de RP que de alguna
manera responden a lo planteado por Pólya sobre“cómo plantear y resolver
problemas”, allí plantea las célebres cuatro fases para enfrentar un problema.
A base de este principio o esquema, diferentes autores plantearon sus propias
teorías añadiendo algunas etapas al proceso y en otros casos procurando depurar
y perfeccionar las ya planteadas.
En este sentido es
preciso citar a Mason, Burton y Stacey, Bransford y Stein, Shoenfield y Miguel
de Guzmán. Investigadores como Barrantes (2008) apoyado en Bay (2000) afirman
que la resolución de problemas es usada por los profesores en el aula de clase
en torno a tres posturas; enseñar para resolver problemas, enseñar acerca de la
resolución de problemas y enseñar mediante la resolución de problemas. De
acuerdo a la primera postura el objetivo es exponer y describir conceptualmente
un objeto matemático que viene seguido de un sin número de ejercicios para
posteriormente plantear situaciones que describan lo estudiado.
La segunda postura se
centra en lo que tiene que ver con la adquisición de una habilidad mediante
estrategias o heurísticas que faciliten la resolución de problemas mediante el
uso de herramientas matemáticas. Y finalmente la resolución de problemas como
vehículo para el aprendizaje, que consiste en enseñar los contenidos
matemáticos mediante el planteamiento y la resolución de situaciones en las
cuales dialogan los objetos matemáticos con el mundo real, para ello el
profesor induce una problemática o situación problema que involucra el eje
temático de la clase y mediante ella se desarrollan los contenidos
curriculares.
En conclusión, las
concepciones se presentan como un condensado de posturas que un profesor
antepone para realizar su intervención en el aula, es así como estas actitudes
referentes a la enseñanza y aprendizaje configuran la estructura conceptual y
las estrategias como docente (Contreras y Carrillo, 1995). En este sentido, se
hace evidente la necesidad de indagar sobre el modelo de formación de
profesores situado desde en un componente específico como lo es la RP, y en
función de ello, se puede abordar como campo de investigación y no remitirse
solamente a una aplicación de conocimientos adquiridos, sin dejar a un lado
métodos, algoritmos o los procedimientos rutinarios ratificadores de un dominio
conceptual. (Puig citado en Cortés y Sanabria, 2012).
Metodología
Esta investigación tiene
un enfoque cualitativo, porque “está orientada a la comprensión, cuyo objetivo
es describir e interpretar la realidad educativa desde dentro” (Sabariego, 2009,
p. 281); y tiene que ver con la forma cómo los estudiantes
comprenden/construyen los conceptos de: límite, derivada, e integral definida,
mediante el planteamiento y resolución de problemas y el papel que la RP juega
en la enseñanza y aprendizaje en estudiantes de tercer año de Licenciatura de
Matemáticas.
Este estudio está
sustentado en un método de investigación etnográfico ya que este tipo de
investigación es “el más conocido y utilizado en el campo educativo para
analizar la práctica docente, describirla desde el punto de vista de las
personas que en ella participan y enfatizar las cuestiones descriptivas e
interpretativas” Sabariego, M. (2009). Otros la definen como el método
investigación por el que se aprende el modo de vida de una unidad social concreta,
por ejemplo, un claustro de profesores o una escuela. Para ello se llevan a
cabo registros del que hacer del profesor en periodos largos de tiempo a través
de la observación en el aula, entrevistas, revisión de materiales, y registros
de audio y video; esto permite dar explicaciones de práctica escolar estudiada.
La población está
constituida 52 profesores, de los cuales se determinaron dos (2) profesores, ya
que estos son lo que orientan las variables de formación (Cálculo Diferencial y
Cálculo Integral) en el Programa de la Licenciatura en Matemáticas y
constituyen la unidad de análisis para el proceso de investigación. Para el
diseño metodológico se tuvieron en cuenta las fases de la investigación
etnográfica (Murillo y Martínez, 2010): Selección del diseño; determinación de
las técnicas; acceso al ámbito de investigación; selección de los informantes;
recogida de datos y la determinación de la duración de la estancia en el
escenario; procesamiento de la información recogida; y elaboración del informe.
El diseño se sintetiza en las siguientes fases y en el esquema la figura 1:
Fase 1.Planeación: Consiste en el planteamiento del problema, formulación de
los objetivos, definición del marco teórico, y el diseño metodológico incluidos
los instrumentos y las técnicas de análisis. Fase 2. Ejecución: acceso al
ámbito de investigación, selección de informantes (profesores y estudiantes) y
trabajo de campo. Fase 3. Análisis: hace referencia al procesamiento de la
información obtenida a partir de los instrumentos previamente establecidos
(diarios de campo, preparadores de clase de los profesores, apuntes de clase de
los estudiantes, entrevistas semiestructuradas, y finalmente la observación y
el registro de episodios en audio y video) y mediante el método de la triangulación.
Fase 4. Informe.
Las técnicas utilizadas
en este estudio etnográfico fueron: La observación no participante, diario de
campo y entrevista semiestructurada. De acuerdo con la literatura existente se
consolidaron las categorías y subcategorías adaptadas de Cortés y Sanabria
(2012).
Tabla 2: Categorías de
análisis
|
Categorías
|
Subcategorías
|
|
Posturas
sobre las matemáticas:
|
Concepciones
sobre el sentido de las matemáticas.
Concepciones
sobre la naturaleza de las matemáticas.
Filosofía de
las Matemáticas.
|
|
Posturas sobre la práctica
educativa:
|
Concepciones
sobre el estudio y preparación en matemáticas (Flores, 1998).
Concepciones
sobre la adaptabilidad a las situaciones en contexto.
Concepciones
sobre la didáctica de las matemáticas presente en el Cálculo.
Concepciones
sobre su intervención en el aula (Contreras y Carrillo, 1995).
Concepciones
que poseen los profesores en la enseñanza y aprendizaje de del Cálculo,
ligadas a los mismos significados sobre las matemáticas.
Concepciones
sobre el currículo del programa.
Concepciones
sobre la finalidad de aprender Calculo Diferencial e Integral.
Concepciones
sobre la reflexión de la práctica docente.
|
|
Posturas sobre el planteamiento y la
resolución de problemas:
|
Concepciones
sobre la resolución de problemas.
Significado
de resolver problemas de acuerdo con el uso que se les ha dado (Vilanova et.
al., 2001).
Concepciones sobre que es un ejercicio,
problema en matemáticas, y situaciones problema.
Concepciones
sobre los modelos para la resolución de problemas.
Concepciones
sobre el objetivo de la resolución de problemas en los estudiantes.
Concepciones
que
posee el profesor frente aspectos epistemológicos en la resolución de
problemas.
Concepciones
sobre el propio significado de resolver problemas.
|
Fuente: Autores
El procesamiento de la
información recogida mediante el diario de campo permitió, establecer
categorías de análisis que luego fueron trianguladas con otros instrumentos
utilizados durante el trabajo de campo, con el propósito de desarrollar una
comprensión sistemática para identificar los patrones que configuran las
concepciones y el modelo de resolución de problemas adoptan en el aula de clase
para determinar el conocimiento, la experiencia, las acciones, las
metodologías, las técnicas, los recursos, el contrato didáctico, las variables
didácticas, la transposición didáctica, y la interacción, para acercarnos a una
trayectoria real sobre la enseñanza del Cálculo a través de la RP y dejar de
alguna manera plasmado un modelo de RP aplicado a la enseñanza de conceptos en
esta área del conocimiento.
Resultados y discusión
En este apartado los
resultados y la discusión se presentan en función de los episodios de dos
profesores en una clase de cálculo diferencial e integral respectivamente
durante dos horas de clase en el primer semestre de 2017. La información
obtenida y el registro de estos episodios se obtuvieron a partir de un registro
en un diario de campo configurado por las notas de clase de los profesores, los
apuntes de los estudiantes y una entrevista semiestructurada a los profesores.
En este sentido, los dos episodios son presentados y discutidos mediante la
triangulación de la información obtenida de estos instrumentos mencionados como
se presenta en la siguiente tabla
Tabla 3: Episodio de
clase Calculo Diferencial
|
Descripción (situación)
|
Argumento (Visión del
etnógrafo)
|
|
El profesor anuncia comenzará con la
unidad de funciones, y enfatiza en que será una de las dos clases más
importantes del semestre junto con la clase de derivadas también argumenta
que debido a que la materia prima del cálculo son las funciones, se resume
así el trabajo para las siguientes tres asignaturas de cálculo siguientes.
El profesor inicia con la definición de Relación
entre dos conjuntos. Para ilustrar lo anterior plantea un
ejemplo sobre la relación entre jugadores de futbol activos nacidos en
Colombia y equipos europeos de futbol donde participaron.

Figura 2: Apuntes
de un estudiante
El profesor copia en el tablero la
definición de Función y pide a sus estudiantes relacionar las
dos últimas definiciones y muestra como el ejemplo anterior NO es una idea
de función. Seguidamente el docente ejemplifica la relación que
existe entre el jugador y el número que utiliza en su camiseta, siendo este un
ejemplo de función.
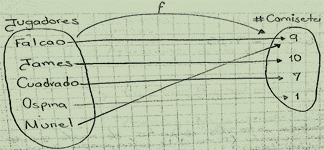
Figura 3: Apuntes
de un estudiante
|
El profesor establece una relación entre
los propósitos del curso y el tema con el que comenzará el espacio académico
de Cálculo Diferencial, permitiendo a los estudiantes establecer las
finalidades de su formación.
El docente parte de hacer énfasis en los
conocimientos básicos o iniciales del Cálculo para captar la atención sobre
la importancia de la Unidad para el desarrollo de toda la línea de los
Cálculos
El docente utiliza una situación real
asociada a un deporte para ejemplificar relaciones entre conjuntos.
Posteriormente evidencia que la situación de los jugadores y equipos no
es ejemplo de función debido a que no cumple la definición formal de
función.
El docente plantea una situación nueva
pero en el mismo contexto deportivo, esta permite al estudiante evidenciar un
ejemplo de función para una situación de su cotidianidad, en ella puede
captar como se satisface la definición formal de función mediante la relación
de dos características que se corresponden con una determinada
particularidad biunívoca.
|
Fuente: Autores
Tabla 4. Episodio 2
cálculo diferencial
|
Descripción (situación)
|
Argumento (Visión del
etnógrafo)
|
|
El profesor plantea ejemplo relacionado
con el número de esposas permitidas en Colombia ante la ley, donde un hombre
corresponde a una sola mujer para contraer matrimonio. El docente plantea el
interés de funciones que relacionan números reales establecidos mediante una Regla
de correspondencia, ecuación, así como a gráfica en el plano
cartesiano. A continuación el profesor plantea un ejemplo: La ecuación  asocia salarios
con descuento por salud y pensión asocia salarios
con descuento por salud y pensión
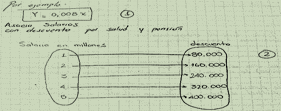

Figura 4: Apuntes
de un estudiante
|
Este ejemplo de las esposas permitidas
por la ley es contrastado con otros países donde la misma situación cambia de
ser función a relación, pues es permitido tener varias parejas en matrimonio,
dando al estudiante la posibilidad de extrapolar el concepto a diferentes
ámbitos.
El docente plantea una situación que
tiene que ver desde lo cotidiano pero articulado en el contexto matemático,
que asocia una función lineal con salarios y descuentos de salud y pensión
propios de los trabajadores Colombianos. De esta manera el profesor liga
situaciones reales para poder ejemplificar las definiciones y a su vez
relacionar representaciones de tipo algebraico, gráfico y simbólico, que
constituyen la construcción de nuevos conceptos e ideas en torno al eje
temático de la clase, logrando mostrar a sus estudiantes las tres formas de
representación de una función (Regla de correspondencia, Diagrama sagital, y
Grafica cartesiana).
Finalmente el profesor expone a sus
estudiantes la definición formal de función real y notaciones funcionales, lo
que permite evidenciar que para esta sesión la metodología del docente es
expositiva referente al manejo de definiciones y ejemplos asociados a
situaciones reales que permiten a los estudiantes mediante un proceso
inductivo y una serie de cuestionamientos, adquirir ideas pragmáticas sobre
la formalidad de las definiciones.
|
Tabla 5. Episodio de
clase Cálculo Integral
Fuente: Autores
|
Descripción
(situación)
|
Argumento
(visión del etnógrafo)
|
|
En
la clase anterior el profesor expone (teorema fundamental de cálculo parte I
y teorema fundamental del cálculo parte II) en función de ello hace estudio
previo de temáticas: Definición de relación inversa de la integral y la
derivada, teorema fundamental de cálculo parte I, teorema fundamental del
cálculo II. Posteriormente al enunciado del teorema y sus respectivas
demostraciones se hacen ejercicios. A continuación el docente
asigna diferentes ejercicios para practicar lo visto en la clase. Para la sesión
actual el docente saluda a sus estudiantes y les pregunta sobre dudas que
puedan haber tenido con los ejercicios de integración de acuerdo con las dos
partes del teorema fundamental del Cálculo vistos en la clase anterior. Paso
siguiente rememora el teorema con dos ejemplos:

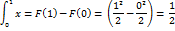
|
El docente expone teoremas con sus
respectivas demostraciones ejemplificadas con ejercicios para ilustrar su
utilidad y algoritmo respectivo. Esto según Blanco (1993) se constituye como
una herramienta que procura resolver, evocar o rememorar un objeto
matemático en específico. Acorde a Benítez (2013) se evidencia una enseñanza
caracterizada por el seguimiento de reglas y procedimientos a partir de una
lectura de conceptos matemáticos y ejercitación mediante la cual el
estudiante debe adquirir la destreza y dominio de los mismos.
Destaca la importancia de
los teoremas fundamentales al permitir calcular integrales sin recurrir a sumas
de Riemann, y añade “al terminar la definición de integral definida verán que
tiene muchas representaciones o aplicaciones como áreas, volúmenes, centros de
masa, puntos de inercia” Enlaza la clase anterior a la actual mediante
ejercicios que ilustran el algoritmo de integración, para este caso un
ejemplo de antiderivación y otro de integración definida que ponen de
manifiesto la importancia del dominio conceptual que enfatiza el docente.
|
Tabla 6. Episodio
de clase Cálculo Integral
Fuente: Autores
|
Descripción
(situación)
|
Argumento
(visión del etnógrafo)
|
|
Después de realizar algunos ejercicios
de evaluación de integrales, el docente plantea un ejemplo de área bajo la
curva, para lo cual solicita a sus estudiantes determinar la suma de Riemman
con una partición regular y luego resolver el problema usando integral
definida:
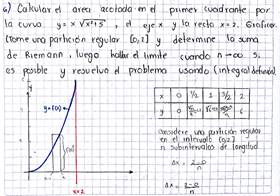
Figura 6: Apuntes
de los estudiantes
A continuación el docente presenta a sus
estudiantes una “aplicación” de la integral definida “desplazamiento o cambio
de posición de una partícula” y realiza un ejemplo.
Paso siguiente el profesor expone una
definición que nombra como otra aplicación:

Figura 7: Apuntes de los estudiantes
|
El
docente mediante este ejemplo ilustra el paralelo que existe entre resolver
el problema de área bajo la curva mediante sumas de Riemann y el uso del
último teorema visto (teorema fundamental del cálculo); mediante la
aproximación de la suma de Riemann los estudiantes evidencian que el proceso
de resolver el problema se hace con una suma finita de particiones (que
representan áreas) y que al tomar el limite cuando la parición tiende a cero
puedo hallar el área exacta. Posteriormente el profesor plantea el problema
por el método de integración definida y enfatiza que es fundamental que se
vea el proceso mediante el cual el límite de una suma de Riemann representa
una integral definida.
El
profesor después de exponer problemas de área bajo la curva que ilustran la
utilización de integrales definidas, afirma que se estudiaran aplicaciones
que requieren del uso de integrales, estas dan desde diferentes situaciones
un contexto de lo que significa resolver una integral (Aldana y
González, 2016). El docente parte de un ejemplo del contexto físico para
relacionar el objeto matemático con su aplicación desde otra disciplina, este
ejemplo es resuelto en clase.
En
congruencia con lo anterior, el profesor plantea otro ejemplo también
relacionando el uso del objeto matemático en cuestión con una aplicación
física, para este caso el cómo está definida la Densidad Lineal en términos
de una integral definida.
El
profesor relaciona las aplicaciones del objeto matemático a diferentes
disciplinas (física, estadística), esto lo hace mediante definiciones de
otros contextos que vinculan el uso de integrales definidas para resolver
situaciones propias del mundo real.
|
En función de la
sesión abordada, los referentes teóricos de apartados anteriores y las
temáticas evidenciadas, es posible situar el desarrollo de clase a la luz de la
bibliografía encontrada. A partir de ello se constata, que el profesor 1 concibe la
resolución de problemas desde su praxis educativa como contexto para enseñar
matemática, es decir, mediante el uso de situaciones reales y pragmáticas
ejemplifica e ilustra la formalidad de las definiciones (Stanic y Kilpatrick, 1989).
Esto en concordancia con investigaciones como Cortés y Sanabria (2012)
evidencian que el profesor de matemáticas no plantea un modelo didáctico o
instruccional basado en la resolución de problemas.
Para el caso del
profesor 2 se concibe la resolución de problemas como habilidad (Stanic y
Kilpatrick, 1989), es decir, después de un estudio conceptual a profundidad en
el cual se desarrollan definiciones, teoremas y demostraciones, el docente
plantea ejercicios de práctica y problemas de habilidades básicas que
posteriormente se reflejan en una “aplicación”, lo anterior de acuerdo con
Barrantes (2008); Bedoya y Ospina (2014) evidencia que la postura que toma el
docente en el desarrollo en sus clases consiste en resolver problemas a partir
de un aprendizaje conceptual.
Además
de lo anterior, junto con el desarrollo de clase de los cursos, es evidente que
en el trasfondo de cualquier modelo de enseñanza de las matemáticas existe una
filosofía de las matemáticas que permea su práctica pedagógica y conforman un
sistema de creencias (Benítez, 2013).
|
Descripción:
|
|
Dado
que la finalidad de la entrevista gira en torno a conocer el pensamiento del
profesor respecto a su modelo de enseñanza del Cálculo Diferencial e
Integral, así como su postura frente al papel de la resolución de problemas,
se muestran las tendencias de los docentes en función de dos preguntas
conductoras:
¿Cuál
es su mejor estrategia para enseñar los conceptos del Cálculo Diferencial e
Integral? y ¿Por qué? ¿Qué función cumple la resolución de problemas como
estrategia y competencia matemática en los estudiantes?
|
|
Tendencia:
|
|
¿Cuál
es su mejor estrategia para enseñar los conceptos del Cálculo Diferencial e
Integral? y ¿Por qué
|
Los
profesores afirman que la mejor estrategia engloba temáticas, desde el
momento que se habla de funciones o antiderivación estar recordando que el
tema de funciones (CD) – antiderivada (CI) se requiere para lo que viene,
efectivamente cuando ve limites (CD) – notación sigma (CI) destaca nuevamente
la importancia de las funciones o la antiderivadación pero aclarando que el tema
de límites (CD) va a ser el tema fundamental en derivada, porque las
derivadas se definen como límites, cuando se está en derivadas entonces
afirman “mire la importancia de los limites acá” “mire que las derivadas se
le calculan a funciones”. En el caso de la notación sigma (CI) se debe
destacar su importancia puesto que permite comprender porque la integral
definida es el resultado de tomar el límite de una suma de Riemann. De ahí se
plantean problemas de aplicación por ejemplo que se resuelven con derivadas
(CD), desplazamiento de partículas, centros de densidad, crecimientos
poblacionales que se resuelven con integrales definidas (CI) entonces eso
despierta el interés, más allá lo que se hace es recordar que aparte de todas
las aplicaciones que tienen, el Cálculo Integral y las Ecuaciones
Diferenciales dependen de lo que se haga en cálculo diferencial y cómo se
conecta la temática, pues deja ver que no son aisladas y todo está conectado.
|
|
¿Qué
función cumple la resolución de problemas como estrategia y como competencia
matemática en los estudiantes?
|
Los
profesores afirman que lo primero que tiene que hacer un estudiante es
conceptualizar, y cuando tiene claro el concepto entonces una forma de
verificar es enfrentándose a diferentes tipos de ejercicios y problemas, y
hay unos que son problemas porque hay un contexto involucrado, donde hay que
obligar al planteamiento de una ecuación, a la deducción o construcción de
una ecuación y pues todo eso ayuda a que los conceptos vayan quedando más
claros, tiene su momento y si en una de esas el estudiante observa que lo que
está estudiando tiene una aplicación, permite resolver un problema de otras
ciencias, de otras disciplinas, magnifico, pero pues no pasa de ahí. Es
decir, aseveran es importante pero no es lo más importante, es una de las
cosas que hay que hacer que se puede implementar y no con todos los temas, en
el caso de la licenciatura en matemáticas.
|
Fuente: Autores
Conclusión
Las concepciones que
tienen los profesores sobre la RP tanto en la enseñanza del Cálculo diferencial
como integral, están ligadas desde el aspecto teórico a la forma de organizar
la enseñanza de un concepto o entidad matemática, es decir, que para ellos la
RP es parte fundamental de la transposición didáctica, pero que a la hora de
enseñar, este proceso está asociado a las aplicaciones que pueda tener el
objeto matemático.
Las prácticas matemáticas
que ejerce el profesor universitario sitúan la RP como un proceso que es
inherente a la enseñanza y al aprendizaje, que viene despues de haber visto una
teoría, un teorema, una demostración, enunciado, axioma o postulado; pero no
constituye el punto de partida de una enseñanza problémica de la cual emerge un
concepto matemático concreto, asociado a estructuras matemáticas con sentido y
significado en contextos de aprendizaje situados.
Las concepciones de los
profesores universitarios sobre las matemáticas, las prácticas educativas y la
misma resolución de problemas, están ligadas a su formación y experiencia
profesional, más que a un proceso consciente de la necesidad de cambiar las
formas de considerar las trayectorias que sigue un aprendiz a la hora de
acercarse a un objeto matemático del conocimiento; no obstante, las evidencias
obtenidas a partir del estudio etnográfico permiten inferir que el docente
universitario concibe la matemática como una articulación entre el aprendizaje,
el saber y la enseñanza; triada en la cual asume otra concepción sobre la RP
como agente de motivación para el aprendizaje.
Referencias
bibliográficas
Aldana, E. y González, M. T. (2016). La
función valor absoluto y el desarrollo del esquema de la integral definida. Artículo
de investigación Revista Electrónica de Investigación en Educación en
Ciencias 11(1). 8-17.
Barrantes Campos,
H. (2008). ¿Qué es un problema matemático? Percepciones en la enseñanza
media costarricense. Cuadernos de investigación y formación en educación
matemática 3(4), 83-98. Recuperado de https://revistas.ucr.ac.cr/index.php/cifem/article/download/6902/6588
Bedoya Echavarría,
M. M. y Ospina Sánchez, S. A. (2014). Concepciones que poseen los profesores
de matemática sobre la resolución de problemas y cómo afectan los métodos de
enseñanza aprendizaje. Tesis de maestría. Universidad de Medellín, Medellín
– Antioquia, Colombia. Recuperado de http://repository.udem.edu.co/bitstream/handle/11407/300/Concepciones%20que%20poseen%20los%20profesores%20de%20matem%C3%A1tica%20sobre%20la%20resoluci%C3%B3n%20de%20problemas%20y%20c%C3%B3mo%20afectan%20los%20m%C3%A9todos%20de%20ense%C3%B1anza%20y%20aprendizaje.pdf?sequence=1
Benítez Chará, W. (2013).
Concepciones sobre las matemáticas, su enseñanza y su aprendizaje de docentes
en formación. Revista Científica, 0, 176 - 180.
Benítez Mojica, D.
y Londoño Millán, N. (2009) Situaciones Problemáticas en Contexto en el
Aprendizaje del Cálculo. El Cálculo y su Enseñanza., México D.F: Cinvestav
del Instituto Politécnico Nacional
Bisquerra, R. et al. (2009). Metodología
de la investigación educativa. Barcelona: Editorial La Muralla, 2da
edición.
Blanco, L.J.
(1993). Una clasificación de problemas matemáticos. Épsilon 25. 49-60.
Contreras, L y Carrillo, J. (1995). Un
modelo de categorías e indicadores para el análisis de las concepciones del
profesor sobre la matemática y su enseñanza. Educación Matemática,
17(3), 79-92.
Cortés,
J, y Sanabria, F. (2012) Concepciones y Creencias de Profesores de
Matemáticas sobre Resolución de Problemas: un estudio de casos. Universidad
del Valle, Santiago de Cali, Colombia
Chevallard, Y. (1991). La transposición
didáctica: del saber
sabio al saber
enseñado. Buenos Aires: Aique.
Flores,
P. (1998). Libro Concepciones y creencias de los futuros profesores sobre
las matemáticas, su enseñanza y aprendizaje. Universidad de Granada,
departamento de didáctica de la matemática, España.
García, Luis, Azcárate, Carmen, y Moreno, Mar. (2006). Creencias,
concepciones y conocimiento profesional de profesores que enseñan cálculo
diferencial a estudiantes de ciencias económicas. Revista latinoamericana de
investigación en matemática educativa, 9(1),
85-116. Recuperado en 16 de abril de 2017, de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-24362006000100005&lng=es&tlng=es
Gil Cuadra, F y Rico Romero L. (2003).
Concepciones y creencias del profesorado de secundaria sobre enseñanza y
aprendizaje de las matemáticas. Enseñanza de las ciencias, 21 (1),
27-47.
Godino, J., Batanero, C., Rivas, H., y
Arteaga, P. (2013). Componentes e indicadores de idoneidad de programas de
formación de profesores en didáctica de las matemáticas. Madrid: Trillas.
Llinares, S. (1991). La Formación de
profesores de matemáticas. Sevilla: GID.
López, E. M., y
Contreras, L. C. (2014). Análisis de los problemas matemáticos de un libro de
texto de 3º ESO en relación con los contenidos de geometría plana. En M. T.
González, M. Codes, D. Arnau y T. Ortega (Eds.), Investigación en Educación
Matemática 18(). 425-434.
Martínez Lozano,
J., & Vergel Ortega, M., & Zafra Tristancho, S. (2015). Validez de
instrumento para medir la calidad de vida en la juventud: vihda. Revista Logos,
Ciencia & Tecnología, 7 (1), 17-26.
Moreno, M. y Azcárate Giménez, C. (2003).
Concepciones y creencias de los profesores universitarios de matemáticas
acerca de la enseñanza de las educaciones diferenciales. Enseñanza de las
Ciencias, 21 (2), 265-280.
Murillo,
J y Martínez, C (2010). Investigación etnográfica, métodos de investigación
educativa. México:Printed
Pajares M. F.
(1992). Teacher`s beliefs and educational research: cleaning unp a messy
contruct. Review
of Educational Research, 62 (3), 307-332.
Pino,
J. (2012). Concepciones y prácticas de los estudiantes de pedagogía media en
matemáticas con respecto a la resolución de problemas y, diseño e
implementación de un curso para aprender a enseñar a resolver problemas. (Tesis
Doctoral no publicada), Badajoz: Universidad de Extremadura.
Pólya,
G. (1954). How
to solve it,
Princeton: Princeton University Press.
Ponte J. P. (1994).
Knowledge, beliefs and conceptions in mathematics teaching and learning. En L.
Bazzini (ed.), Theory and practice in mathematics education. Proceedings of
the Fifth internacional conference on systematic cooperation between
theory and practice in mathematics education. Grado, Italia.
Porlán, R. (1992). Teoría y práctica
del curriculum. El curriculum en la acción. En AA.VV, Curso de actualización
científico-didáctica. Madrid: MEC.





