Fecha de recepción del artículo: 07 de Agosto de 2017
Fecha de aceptación del artículo: 21 de Diciembre de 2017
DOI: http://dx.doi.org/10.22335/rlct.v10i1.440
*El artículo es resultado de investigación: Modelo matemático para minimizar el número de láminas estándar y residuos metálicos durante el proceso de corte en el sector metalmecánico”.
** Ingeniera Química, Universidad del Valle, Colombia. Magister en Educación, Pontificia Universidad Javeriana Cali, Colombia. Docente de planta, Facultad de Ingeniería, Pontificia Universidad Javeriana Cali. Correo electrónico: gportillaw@gmail.com Orcid: https://orcid.org/0000-0002-3243-7659
Resumen
En esta propuesta para el desarrollo profesional de los profesores a partir de una revisión a estudios concernientes al carácter social de aprender, junto con el desarrollo histórico- epistemológico de conceptos, se indaga la relación entre las progresiones geométricas y aritméticas y, se realiza una invitación de aprendizaje dirigida a los profesores de Precálculo. Ella lleva entrelazado un ambiente de laboratorio, haciendo uso de sensores y apps, en el análisis de los casos de la escala logarítmica musical y del pH. Se usa la metodología de análisis de contenido con el fin de esbozar caminos concernientes a ¿De qué maneras, los profesores universitarios de Precálculo, pueden acercarse a la comprensión y caracterización de las funciones logarítmicas?
Palabras clave: sensores, apps, escala logarítmica, profesor, social, formación.
Abstract
In this proposal for teacher’s professional development from a revision of some studies regarding the social character of learning, along with development of historic –epistemological concepts, it is explored the relation between geometrical and arithmetical progressions and it is extended an invitation of learning addressed to Precalculus teachers. This one has intertwined a laboratory environment, making use of sensors and apps, in the analysis of logarithmic musical scale cases and in the pH. It is used the content analysis methodology with the purpose of sketching some ways with regarding to the question: In which ways the Precalculus university teachers are able to approach to the comprehension and characterization of the logarithmic funtions?
Key Words: sensors, apps, logarithmic scale, teacher, social, formation
Resumo
Na presente proposta para o desenvolvimento profissional de professores a partir de uma revisão a estudos concernentes ao caráter social de aprendizagem, junto com o desenvolvimento histórico-epistemológico de conceptos, se indaga a relação entre as progressões geométricas e aritméticas e se realiza uma compra de aprendizagem dirigida aos profesores de Precálculo. Ella leva entrelazado um ambiente de laboratório, fazendo uso de sensores e aplicações, em análise dos casos da escala logarítmica musical e do pH. Se usa a metodologia de análise de conteúdo com o final de esbozar caminos concernentes a ¿De quais maneras, os professores universitários de Precálculo, podem aproximar a comprensão e caracterização das funções logarítmicas?
Palavras-chave: sensores, apps, escala logarítmica, professor, social, formação.
Introducción
La utilización de modelos matemáticos en empresas dedicadas a la fabricación de productos metálicos para el hogar, permite, entre múltiples aplicaciones, optimizar el consumo de materia prima (Cueli, et. al., 2016), lo que a su vez se traduce en la minimización de residuos, llevando a las empresas a mejorar sus beneficios económicos y a reducir los impactos ambientales negativos en su entorno (Donini & Micheletto, 2015). Este modelo se centra en minimizar el número de láminas estándar utilizadas en el proceso de corte para una demanda determinada de uno de los productos.
Para aplicar los modelos matemáticos de programación lineal se seleccionó una de las empresas del sector metalmecánico del municipio de Palmira, ubicado al sur del departamento del Valle del Cauca, Colombia, y que según proyección del Departamento Nacional de Estadística cuenta con una población cercana a los 302.000 habitantes. En este municipio, la industria metalmecánica es la segunda gran generadora de empleo.
La empresa seleccionada se denominará “empresa piloto”. Esta empresa fabrica armarios, gabinetes y alacenas metálicas dirigidos a mercados de estratos medio y bajo. Los productos se distribuyen en municipios colombianos de los departamentos del Valle del Cauca, Quindío, Risaralda, Cauca y Nariño.
De los diversos productos fabricados por la empresa se eligió un tipo de armario metálico que registra la mayor demanda general. Este producto utiliza para su fabricación una clase de lámina de acero estándar, a partir de la cual se realizan los diferentes cortes de las nueve piezas que lo integran y que posteriormente se unen para darle el acabado final y lograr el producto terminado.
Metodología
Inicialmente se contactó a la “empresa piloto” y se indagó sobre el proceso de fabricación de sus productos. Dada la variedad de sus productos, se concertó realizar el estudio sobre un modelo de armario de gran aceptación y amplia demanda (Hernández y Rojas, 2016). El proceso de fabricación de este armario tiene como materia prima principal láminas de acero que el mercado ofrece en un tamaño estándar de 1250 mm x 2450 mm. Los operarios de turno, tomando como criterio su experiencia, programaban los cortes a realizar en cada lámina para obtener las distintas piezas que conforman el armario. Este criterio subjetivo no garantiza eficiencia, es decir que se utilicen menos recursos para lograr el objetivo (García, Rizo, y Arroyo, 2016; (García, Rizo, y Arroyo, 2013), y, es por ello que se seleccionó esta etapa del proceso general para aplicar la modelación matemática que minimice el número de láminas requeridas para la producción de los armarios.
El proceso general de fabricación del producto está integrado por siete pasos: Recepción y almacenamiento de láminas metálicas estándar, Corte de lámina y generación de residuos de lámina, Doblado de partes, Soldadura, Acabado, Almacenamiento y Despacho. La figura 1, muestra el diagrama general para la fabricación de un armario.
El diseño del modelo matemático corresponde a la sección de corte de lámina y generación de residuos de lámina. El modelo matemático tiene como objetivo minimizar el número de láminas necesarias para fabricar los armarios demandados por semana, lo que lógicamente traerá beneficios económicos para la empresa ya que este proceso se repite varias veces por día, además de producir menor cantidad de residuos metálicos, beneficiando al medio ambiente y contribuyendo con el compromiso de responsabilidad ambiental de la empresa.
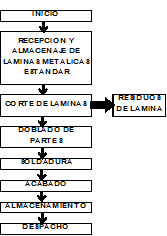
Figura 1. Flujo del proceso para manufactura de armarios metálicos. Fuente: Autora
Una vez seleccionado el armario a estudiar, que en adelante se denominará producto, se identificaron y cuantificaron las dimensiones y área de cada una de las nueve piezas que integran este producto para conformar los moldes base de cada pieza. Estos moldes se superponen en la lámina metálica estándar, para diseñar las diferentes combinaciones factibles que permitan extraer el mayor número de piezas por lámina. Cabe aclarar que aunque la empresa dispone de algunos moldes estándar, se observó que no son dispuestos adecuadamente en el área total de la lámina, produciendo sobrantes que, en algunos casos, si se dispusieran de manera diferente, podrían utilizarse para el corte de piezas menores o para lograr mayor número de piezas.
El producto seleccionado contiene nueve piezas de diferentes dimensiones. El esquema general y la distribución y número de piezas se muestran en la Figura 2 y en la tabla 1.
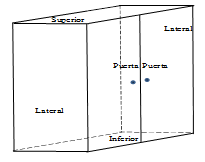
Figura 2. Esquema general de las partes del producto. Fuente: Autora
Tabla 1. Piezas requeridas por unidad de producto
|
Cantidad |
Ubicación |
|
|
P1 |
1 |
Parte superior |
|
P2 |
1 |
Parte inferior |
|
P3 |
4 |
Laterales (2) y divisiones internas (2) |
|
P4 |
1 |
Parte trasera |
|
P5 |
2 |
Puertas |
Fuente: Autora
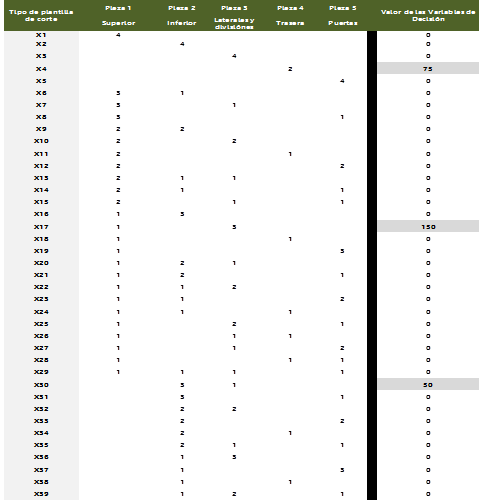
Combinando los moldes de cada pieza y el tamaño de la lámina estándar, se encontraron 51 posibilidades diferentes de plantillas de corte (Xi, i = 1,…, 51), que se describen en la tabla 2. El valor de Xi es un número entero, no negativo, que le indicará al operario el número de láminas estándar que deben cortarse para obtener el número de piezas (P) asociadas a esa plantilla, de acuerdo a las especificaciones de la tabla 1.
Como ejemplo aclaratorio, la plantilla denominada X11 = 2P1 + P4, indica que, por cada lámina asignada a este patrón de corte, se obtienen dos piezas de la parte superior (P1) y una pieza de parte trasera (P4); de igual manera la plantilla identificada como X27 = P1 + P3 + 2P5, entrega una pieza para la parte superior (P1), una pieza lateral o división interna (P3) y dos piezas para puerta (P5), por cada lámina estándar cortada bajo este esquema de plantilla.
Tabla 2. Tipos de patrones o plantillas de cortes posibles en lámina estándar
|
X1 = 4P1 |
X18 = P1 + P4 |
X35 = 2P2 + P3 + P5 |
|
X2 = 4P2 |
X19 = P1 + 3P5 |
X36 = P2 + 3P3 |
|
X3 = 4P3 |
X20 = P1 + 2P2 + P3 |
X37 = P2 + 3P5 |
|
X4 = 2P4 |
X21 = P1 + 2P2 + P5 |
X38 = P2 + P4 |
|
X5 = 4P5 |
X22 = P1 + P2 + 2P3 |
X39 = P2 + 2P3 + P5 |
|
X6 = 3P1 + P2 |
X23 = P1 + P2 + 2P5 |
X40 = P2 + P3 + 2P5 |
|
X7 = 3P1 + P3 |
X24 = P1 + P2 + P4 |
X41 = P2 + P3 + P4 |
|
X8 = 3P1 + P5 |
X25 = P1 + 2P3 + P5 |
X42 = P2 + P4 + P5 |
|
X9 = 2P1 + 2P2 |
X26 = P1 + P3 + P4 |
X43 = P2 + P3 + P5 |
|
X10 = 2P1 + 2P3 |
X27 = P1 + P3 + 2P5 |
X44 = 3P3 + P5 |
|
X11 = 2P1 + P4 |
X28 = P1 + P4 + P5 |
X45 = 2P3 + P4 |
|
X12 = 2P1 + 2P5 |
X29 = P1 + P2 + P3 + P5 |
X46 = 2P3 + 2P5 |
|
X13 = 2P1 + P2 + P3 |
X30 = 3P2 + P3 |
X47 = P3 + P4 |
|
X14 = 2P1 + P2 + P5 |
X31 = 3P2 + P5 |
X48 = P3 + 3P5 |
|
X15 = 2P1 + P3 + P5 |
X32 = 2P2 + 2P3 |
X49 = P3 + P4 + P5 |
|
X16 = P1 + 3P2 |
X33 = 2P2 + 2P5 |
X50 = P4 + 2P5 |
|
X17 = P1 + 3P3 |
X34 = 2P2 + P4 |
X51 = P4 + P5 |
Fuente: Autora
Modelo matemático. Un modelo matemático es una representación matemática de la realidad que puede utilizarse para tomar mejores decisiones o para comprender una situación compleja. El modelo matemático de programación lineal permite encontrar la mejor forma de asignar recursos, generalmente, escasos a diversas actividades que compiten por ellos.
Resultados
Para el caso que se presenta se utilizó la teoría de modelos matemáticos lineales con soluciones enteras. El modelo de programación lineal incluye tres componentes: Variables de decisión, Función objetivo y Conjunto de restricciones:
Variables de Decisión. D: Número de armarios a producir por semana (demanda)
X1, X2, X3, …, X51: Corresponden a las 51 plantillas o patrones de corte por lámina estándar que le indicarán al operario la forma óptima de efectuar los cortes para obtener las piezas necesarias para satisfacer la demanda semanal del producto, utilizando la menor cantidad de ellas. El valor o resultado de cada variable debe ser un número entero por cada tipo de combinación, siendo cero su mínimo valor. Si el valor resultante es cero, indica que este patrón de corte no debe utilizarse.
Función Objetivo: Minimizar el número de láminas de acero estándar necesarias para satisfacer la demanda semanal del producto.
Conjunto de restricciones o limitantes: Obtener, a partir de los patrones de corte por lámina (X1, …, X51), al menos, el número total de piezas necesarias para fabricar el número de unidades de producto demandado por semana.
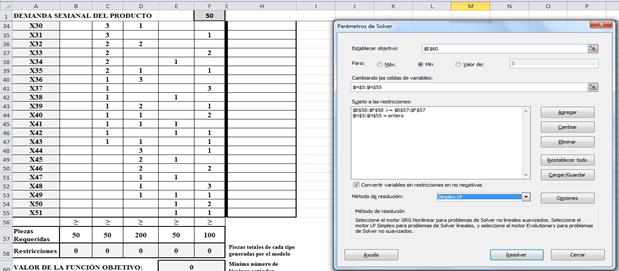
Formulación del modelo matemático de programación lineal. Utilizando el complemento Solver de Microsoft Excel, bajo el método Simplex para obtener su solución. Solver es un programa de complemento de Microsoft Office Excel que está disponible cuando se instala Microsoft Office.
Función Objetivo: El objetivo es minimizar el número total de láminas estándar utilizadas para satisfacer la demanda semanal del producto. Su expresión matemática corresponde a la sumatoria del número de láminas destinadas a ser cortadas de acuerdo a cada uno de los 51 patrones establecidos.
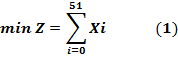
Conjunto de restricciones o limitantes: Las restricciones son expresiones matemáticas formuladas para garantizar que se cuente con el número total de cada una de las nueve piezas necesarias para fabricar el producto, según una demanda dada (D). La formulación es la siguiente:
Patrones de cortes a partir de los cuales se obtiene la Pieza 1 (parte superior):
4X1 + 3X6 + 3X7 + 3X8 + 2X9 + 2X10 + 2X11 + 2X12 + 2X13 + 2X14 + 2X15 + X16 + X17 + X18 +X19+ X20 + X21 + X22 + X23 + X24 + X25 + X26 + X27 + X28 + X29 ≥ D (2)
Patrones de cortes a partir de los cuales se obtiene la Pieza 2 (parte inferior):
4X2 + X6 + 2X9 + X13 + X14 + 3X16 + 2X20 + 2X21 + X22+ X23+ X24+ X29+ 3X30 + 3X31 + 2X32 + 2X33 + 2X34 + 2X35 + X36 + X37 + X38 + X39 + X40 + X41 + X42 + X43 ≥ D (3)
Patrones de cortes a partir de los cuales se obtiene la Pieza 3 (laterales):
4X3 + X7 + 2X10 + X13 + X15 + 3X17 + X20 + 2X22 + 2X25 + X26 + X27 + X29 + X30 + 2X32 + X35 + 3X36 + 2X39 + X40 + X41 + X43 + 3X44 + 2X45 + 2X46 + X47 + X48 + X49 ≥ 4D (4)
Patrones de cortes a partir de los cuales se obtiene la Pieza 4 (parte trasera):
2X4 + X11 + X18 + X24 + X26 + X28 + X34 + X38 + X41 + X42 + X45 + X47 + X49 + X50 + X51 ≥ D (5)
Patrones de cortes a partir de los cuales se obtiene la Pieza 5 (puertas):
4X5 + X8 + 2X12 + X14 + X15 + 3X19 + X21 + 2X23 + X25 + 2X27 + X28 + X29 + X31 + 2X33 + X35 + 3X37 + X39 + 2X40 + X42 + X43 + X44 + 2X46 + 3X48 + X49 + 2X50 + X51 ≥ 2D (6)
Xi, D ≥ 0 ^ Xi, D: entero (7)
Una vez diligenciado este formato, se utiliza el complemento Solver de Excel para ingresar la posición de la celdas que contienen la demanda semanal de producto (F1), las ecuaciones de la función objetivo (E60), conjunto de restricciones
(B58 a F58) y tipo de variables de decisión (H5 a H55). Además debe especificarse que el método de resolución es Simplex y que el objetivo es minimizar. El resultado del modelo de optimización se registrará en las celdas H5 a H55 y B58 a F58. La figura 4 presenta el caso para la demanda de 50 unidades de producto por semana.
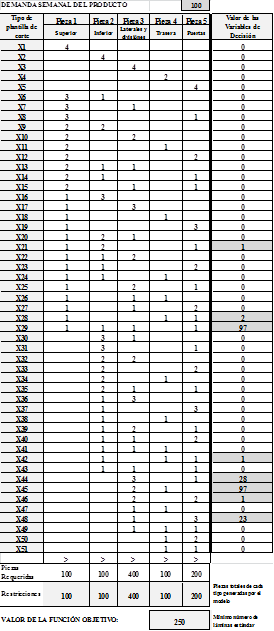
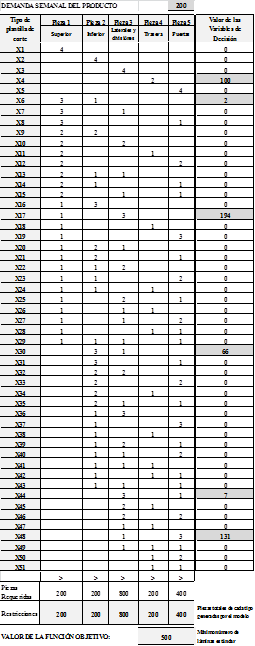
En el formato Excel, en la fila 58 desde la columna B hasta la columna F, se han incorporado las ecuaciones correspondientes a las restricciones del modelo de programación lineal (ecuaciones 2 a 6), que garantizan la obtención del número óptimo de cada tipo de pieza que requiere la producción semanal. Este valor será igual o mayor que el respectivo valor registrado en la fila 57.
En la columna H, desde la fila 5 hasta la 55, se calcula y muestra el número óptimo de láminas estándar destinadas a ser cortadas de acuerdo a cada tipo de plantilla o patrón. De igual manera, en la fila 60, columna E, se presenta la función objetivo (ecuación 1), que cuantifica el número mínimo de láminas estándar requeridas para cumplir con la demanda semanal del producto y que corresponde a la sumatoria de los valores calculados en la columna H, desde la fila 5 hasta la 55.
Para la solución del modelo matemático de programación lineal entera, se ejecutaron simulaciones para demandas de 50, 100, 150 y 200 unidades de producto semanal. A continuación, las figuras 5, 6, presentan los formatos diligenciados y los resultados obtenidos para cada simulación.