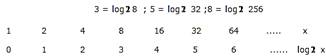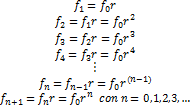Fecha
de recepción del artículo: 07 de Agosto de 2017
Fecha
de aceptación del artículo: 21 de Diciembre de 2017
DOI: http://dx.doi.org/10.22335/rlct.v10i1.420
*El artículo es resultado
de investigación: Formación de profesores Sensores y apps en el estudio de la
escala logarítmica”.
** Doctora en educación
matemática, Universidad de Salamanca. Filiación: Universidad Colegio Mayor de
Cundinamarca. Correo electrónico: jvargash@unicolmayor.edu.co Orcid:
https://orcid.org/0000-0002-8936-696X
***Magister en Docencia
de la matemática. Filiación: Universidad Colegio Mayor de Cundinamarca. Correo
electrónico: rfchavez@unicolmayor.edu.co.
Orcid: https://orcid.org/0000-0003-1998-3345
*** Magister en Docencia
de la matemática. Universidad Pedagógica Nacional. Filiación: Escuela Superior
de Ingeniería. Correo electrónico: luis.jaimes@escuelaing.edu.co.
Orcid: https://orcid.org/0000-0002-2540-6336
Resumen
La investigación buscó
desarrollar una estrategia para el desarrollo profesional de los profesores a
partir de una revisión a estudios concernientes al carácter social de aprender,
junto con el desarrollo histórico- epistemológico de conceptos, indagó la
relación entre las progresiones geométricas y aritméticas y, realiza una
invitación de aprendizaje dirigida a los profesores de pre-cálculo. Ella lleva
entrelazado un ambiente de laboratorio, hace uso de sensores y apps, en el
análisis de los casos de la escala logarítmica musical y del pH. Se usa la
metodología de análisis de contenido con el fin de esbozar caminos
concernientes a ¿De qué maneras, los profesores universitarios de precálculo,
pueden acercarse a la comprensión y caracterización de las funciones
logarítmicas?
Palabras clave: sensores,
apps, escala logarítmica, profesor, social, formación.
Abstract
In
this proposal for teacher’s professional development from a revision of some
studies regarding the social character of learning, along with development of
historic –epistemological concepts, it is explored the relation between
geometrical and arithmetical progressions and it is extended an invitation of
learning addressed to Precalculus teachers. This one has intertwined a
laboratory environment, making use of sensors and apps, in the analysis of
logarithmic musical scale cases and in the pH. It is used the content analysis
methodology with the purpose of sketching some ways with regarding to the
question: In which ways the Precalculus university teachers are able to
approach to the comprehension and characterization of the logarithmic funtions?
Key
Words: sensors, apps, logarithmic scale, teacher, social, formation
Resumo
Na presente proposta para
o desenvolvimento profissional de professores a partir de uma revisão a estudos
concernentes ao caráter social de aprendizagem, junto com o desenvolvimento
histórico-epistemológico de conceptos, se indaga a relação entre as progressões
geométricas e aritméticas e se realiza uma compra de aprendizagem dirigida aos
profesores de Precálculo. Ella leva entrelazado um ambiente de laboratório,
fazendo uso de sensores e aplicações, em análise dos casos da escala
logarítmica musical e do pH. Se usa a metodologia de análise de conteúdo com o
final de esbozar caminos concernentes a ¿De quais maneras, os professores
universitários de Precálculo, podem aproximar a comprensão e caracterização das
funções logarítmicas?
Palavras-chave:
sensores, apps, escala logarítmica, professor, social, formação.
Introducción
En el ámbito de la
educación matemática es claro que las propuestas para el desarrollo profesoral
no incluyen exclusivamente la comprensión de procesos cognitivos de los
estudiantes en su aprendizaje o el conocimiento matemático del profesor, sino
que ellas tratan de impactar en una red de comportamientos del profesor,
construcciones del ser y el re-aprendizaje de diversas habilidades y
componentes implicadas en la planeación y gestión en el aula; que se
materializan en la resolución de problemas del quehacer docente.
Por otro lado, aceptando
a la Educación como sistema formal de preparación del ciudadano, ella debe
aportar elementos formativos para favorecer procesos de interacción humana de
alta calidad que rescaten las diferencias y riqueza del trabajo colaborativo y
cooperativo,
“Las estrategias de
aprendizaje deben ir dirigidas al desarrollo del estudiante entendiendo este
como cambio cualitativo superior al atender, no solo a la utilización de los
factores externos del proceso de enseñanza aprendizaje como recursos, medios,
sino también a los internos como motivación, valores, actitudes, desarrollo
cognoscitivo. Ellas deben generar en los estudiantes autonomía en íntima
conexión con procesos socializadores, desarrollo de procesos del pensamiento
como reflexión, meta cognición, sentimientos, actitudes ante el aprendizaje y
las formas de cooperación en que se pueden obtener, van a ser generadores de
desarrollo de la personalidad convirtiéndose en un proceso de enseñanza
aprendizaje desarrollador, que atienda el carácter complejo del proceso y de la
situación” (González, Recino y Uvaldo, 2013, p. 218).
En el campo de la didáctica
de la matemática, se conoce que el profesor tiene formación en los conceptos de
las funciones, desde los cursos realizados en su educación; en álgebra y
cálculo, entre otros. Al respecto los educadores matemáticos han afirmado que
el estudio de la variación es un camino para examinar las funciones lineales,
cuadráticas, cúbicas, es decir las funciones polinómicas y respecto a las
funciones transcendentes, se ha iniciado desde hace una década un impulso al
estudio de la variación exponencial y logarítmica.
Metodología
El
proceso que se realiza busca alternativas de respuesta a ¿De qué maneras, los
profesores universitarios de Precálculo, pueden acercarse a la comprensión y
caracterización de las funciones logarítmicas?
Se
utilizó la metodología de análisis de contenido identificando diferentes
publicaciones en cuatro temáticas: trabajo colaborativo y cooperativo en la
educación superior, modelación en las clases de matemáticas, desarrollo
histórico-epistemológico de los conceptos, investigaciones relativas a
funciones logarítmicas. En reuniones; una semanal durante un año académico, los
investigadores socializaron sus consultas y en equipo se realizó el análisis de
la documentación leída; se trianguló información de tal manera que se
establecieron los tres contextos reales sobre los cuales se formularían las
actividades de modelación en torno a la formación de docentes.
Se
siguieron dos caminos: Por un lado, se integran estas cuatro temáticas, se
planeó y llevó a término en el primer semestre del año 2015, una experiencias
con 127 estudiantes, en cuyo desarrollo se recoge información alrededor de la
dinámica de trabajo colaborativo. La tarea que el profesor encarga a sus
estudiantes consiste en escribir un cuento, en la cual se contesta a una
pregunta específica sobre la función logarítmica.
El
procedimiento adoptado para esta experiencia se basó en Vargas y Gacharná
(2008) el cual consistió en:
•Lectura
general que han realizado los estudiantes, de primer semestre que cursan
pre-cálculo, del libro El Diablo de los Números.
•Socialización,
de la lectura, en la cual se ha tratado de “explorar” una de las noches y
conversar sobre las características que el escritor presenta, concerniente al
tema matemático. En dichas conversaciones se permiten comentarios adicionales,
con respecto a: dibujos utilizados, diagramas, recursos lúdicos, vocabulario.
•Planteamiento
de una pregunta sobre una característica de la función logarítmica.
•Guía
sobre la lectura intencionada que realizan, los estudiantes tanto en textos de
precálculo como en artículos de revistas especializadas.
•Uso
de palabras clave, entre las cuales están: razón de cambio promedio, función
logarítmica, función exponencial, progresión geométrica, progresión aritmética,
didáctica de la matemática, precálculo.
•A
través del proceso de la escritura, el profesor pretende observar dinámicas de
los grupos en cuanto:
Cuestionamientos
y discusión de los hallazgos. Particularidades de la comprensión que ha
alcanzado el grupo de estudiantes.
De otra parte, de manera
simultánea se avanzó en el delineamiento de los problemas de modelación y en la
escritura de los referentes teóricos, a partir de la comprensión de aspectos de
la función logarítmica y de los contextos en que ella es usada en diferentes
áreas del conocimiento.
La decisión de partir del
referente histórico – epistemológico fue planteada a partir de los estudios
realizados, se utilizó para su validación, la confrontación con otras
propuestas consultadas en la literatura en Educación Matemática. De allí que se
inicie el planteamiento a los profesores a partir lo que se llamó en esta
investigación Revisando Regularidades.
Los análisis
concernientes a lo característico de cada fenómeno o contexto, en relación con
la red de conceptos que integran la comprensión de la función logarítmica y las
escalas, fueron definitivos en las decisiones consensuadas de tres
investigadores y en las preguntas guía para los profesores a quienes va
dirigida la propuesta. Lo anterior ayudó a establecer la experiencia en la cual
se detallarían aspectos del trabajo colaborativo y cooperativo, como también la
secuencia en que serían tratados los fenómenos; escala musical, pH y escala de
Ritcher.
Simultánea a la selección
de fenómenos se fue decidiendo el uso que se llevaría a término de herramientas
tecnológicas que permitieran un ambiente de laboratorio, por ello se trabajó
tanto con los sensores de pH y sonido, como de las aplicaciones para celular y
PC. Se utilizó para la escala pH el software LabQuest Viwer, Logger Lite y
luego en el estudio y explicación de la escala musical se plantea la opción del
software LabQuest Viwer, Logger Lite y se ejemplifica la aplicación Best Tuner
o piano virtual.
Revisando
regularidades
En cuanto a
la formación de profesores y la variación logarítmica en el entorno a la
covariación, consideramos importe las investigaciones sobre el desarrollo
histórico (Vargas Hernández & Gónzalez Astudillo, 2007; Ferrari M., 2007).
Concerniente a la representación gráfica de dicha función se tiene el estudio
que parte de la construcción de triángulos semejantes en López y Ferrari (2007)
y retomando la génesis del concepto en cuanto a su relación entre la progresión
geométrica y aritmética está la propuesta de Vargas Hernández, Pérez Ruiz,
& González Astudillo, (2011) en la cual se presenta un análisis y
construcción de la gráfica, así como un análisis de las exigencias cognitivas
para los docentes de matemáticas, en cuanto a dicha representación gráfica, en
Castañeda, Novoa, & Vargas Hernández (2016).
Desde una
perspectiva histórica, los logaritmos han estado asociados a la relación entre
progresiones aritméticas y geométricas, y algunos autores en el siglo XIX,
incluían estos términos en sus definiciones, llamando logaritmos a los términos
de una progresión aritmética, que empieza por cero, correspondientes a los de
otra geométrica que empieza por la unidad (Vázquez, 1855; González y Vargas,
2007). Trabajar con este tipo de progresiones, se sugiere como un buen inicio
para el estudio de los logaritmos (Vargas, 2013; Vargas, Pérez y González,
2011) por lo anterior, a continuación se presenta una serie de sugerencias para
el docente, de tal forma que partiendo de la identificación de regularidades,
pase a identificarlas y posteriormente establecer su relación, previo e
integrado al trabajo con las funciones exponenciales y logarítmicas.
En razón de
lo expuesto, se propuso el uso de tablas elaboradas en hojas de cálculo, que
permitan identificar al docente, regularidades en cada progresión.
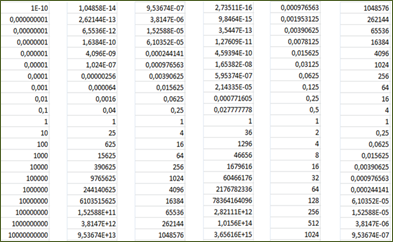
Figura 2.
Tabla para identificar progresiones. Fuente: Autores
Al trabajar
con estas tablas, se plantearon preguntas como ¿Cuál es el patrón que siguen los
datos de la progresión en la primera columna? ¿Al examinar la progresión de la
columna 3, la diferencia entre dos términos consecutivos cuales quiera es
constante o variable? ¿Cuáles progresiones presentan la misma diferencia entre
dos términos consecutivos?, este tipo de acciones son realizadas para encontrar
que la diferencia entre dos términos consecutivos de cualquiera de las
progresiones corresponde a un valor constante, y que progresiones como por
ejemplo las que se encuentran en las columnas 2 y 7, tienen en común esta
diferencia aunque todos sus elementos no sean iguales. También se promueve la
reflexión sobre sus tareas profesionales relativas a la planeación y gestión,
iniciando un trabajo en equipo en el cual los profesores propongan otras progresiones
que consideren pertinentes, a través de preguntas como: ¿alguna de las
progresiones presentadas es demasiado evidente con relación a las preguntas que
se hacen sobre ella?, ¿cambiaría usted las preguntas o las progresiones?
Considera que las respuestas que usted ha aportado, son similares a las que los
estudiantes de pregrado llegarán a exponer o encuentra que debe programar una
guía más específica para que ellos analicen las regularidades. De una forma
análoga se realizó el trabajo con las progresiones geométricas, como se muestra
a continuación:
En relación a
estas progresiones (figura 3), las preguntas a plantear fueron fundamentadas en
orientar al docente a identificar mediante cocientes entre términos
consecutivos la razón de una progresión geométrica, por ejemplo, ¿En la
progresión de la columna 1 (Figura 3), es posible encontrar una diferencia
constante? ¿Cómo están cambiando los términos?
¿Cuál es la
razón entre el término 0.1 y 0.01? ¿Es posible encontrar esta razón con otros
términos de la progresión? ¿Qué sucede en la progresión de la columna 3 (Figura
3) al tomar cualquier término y dividirlo en el término anterior? ?, este tipo de preguntas orientan para encontrar un
comportamiento diferente en los términos de la progresión, pero que de igual
forma al operar dos términos consecutivos (dividir en este caso) es posible
encontrar un patrón.
Progresiones
geométricas
En cuanto a
la notación empleada, se planteó un espacio de discusión con los profesores,
para con el aporte de la literatura en Educación Matemática, decidir los
momentos convenientes de la actividad, para ir presentando y usando la
escritura referida a los n-ésimos términos (…, n, n+1,…) y demás notación
específica de tal forma que al utilizarla se facilite su correspondiente comprensión.
El paso a seguir, es trabajar con dos listados de progresiones, relacionando
sus términos uno a uno, y representando cada par en el plano cartesiano, de tal
forma que se pueda identificar un comportamiento común en la gráfica que
relaciona dos progresiones de este tipo (aritmética y geométrica).
Para iniciar,
las preguntas e indicaciones planteadas en este caso, relacionadas con la
identificación del tipo de progresión y la curva que se obtiene al relacionar
una progresión aritmética con una geométrica, por ejemplo, ¿Es posible
encontrar un patrón en la diferencia o cociente entre dos términos
consecutivos de cada una de estas progresiones?, ¿Qué tipo de progresiones son
Progresiones Aritméticas y Geométricas.?, posterior a las preguntas, se solicita
relacionar cada término de la progresión P.A. con el término correspondiente en
la progresión P.G. y finalmente utilizó la hoja de cálculo para representar
cada uno de estos pares como un punto del plano cartesiano.
De esta
forma, se iniciaría el trabajo previo a los elementos matemáticos relacionados
con funciones exponenciales y logarítmicas.
Mirada con
énfasis en la gestión de la participación del estudiante. El caso de la escala
para el pH.
Desde la
perspectiva de la formación del profesor contempla un amplio espectro de
conocimientos, habilidades, comportamientos y complejidad. Basado en estudios
que desde la didáctica argumentan que se puede promover la formación en los
profesores asumiendo la enseñanza más allá de un arte.
El profesor y
el trabajo colaborativo
Un trabajo en
el aula que busque propiciar una red de interacciones entre estudiantes, en la
cual se involucre un cambio de discurso que establezca un giro en el rol del
profesor de preguntar- escuchar - validar, por un rol en el cual los estudiantes
se sientan invitados a argumentar- escuchar y volver a argumentar, realizando
conjeturas y teniendo la oportunidad de experimentar. Ese es un trabajo puede
tener momentos en los cuales el docente necesite gestionar en el aula la
integración de subgrupos de estudio de los contenidos, de tal forma que un
ejercicio en la formación del profesor es aprender a ser miembro, tanto en un
trabajo colaborativo como en el cooperativo.
La exposición
y análisis de diferencias entre diferencias entre el rol del maestro en el
trabajo colaborativo y cooperativo en Maldonado (2007) y Ibarra-Sáiz y
Rodriguez (2007) son conocimientos que coadyuvan al docente a tener argumentos,
sobre momentos a reformular, en la planificación de sus horas clase.
A partir de
lo anterior, iniciamos en esta sección algunas de las reflexiones y el estudio
que proponemos en la formación de docentes que se desempeñan en el área de
matemáticas en los primeros semestres universitarios (Vargas y Gacharná, 2008).
Los resultados surgen a partir de una tarea en la cual el profesor cumple en
ocasiones funciones semejantes a las de en un trabajo cooperativo y en otros
aspectos son similares a un trabajo colaborativo.
Se considera que
el discurso del profesor se vuelve más flexible y profundo, cuando conoce y
puede experimentar a través de otras situaciones, que no sean solamente su
participación real en clase, sino también los resultados de investigaciones; ya
sean estos presentados a manera de relatos, estudios de caso o resultados
estadísticos. En la experiencia, se planteó una tarea a los estudiantes de
matemáticas de pregrado en su primer semestre de estudios, en I - 2015 y se
llevó a término durante todo el semestre con 127 estudiantes, quienes se
organizaron en grupos de 5 o 6 estudiantes. De los cuales presentamos la
clasificación de la tarea de 7 grupos.
Para la tarea
realizada con la asesoría del profesor, el procedimiento consistió en la
lectura general del libro El Diablo de los Números (Enzenberger, 1998). Sobre
dicha lectura, durante el semestre se ha realizado al menos una socialización
en la cual se ha tratado de “explorar” una de las noches y conversar sobre las
características que el escritor presenta, concerniente al tema matemático. En
dichas conversaciones se permiten comentarios adicionales, con respecto a: los
dibujos utilizados, los diagramas, los recursos lúdicos, el vocabulario, entre
otros.
En la
consulta guiada que el docente organiza, propone a los estudiantes participar
en la indagación sobre las funciones exponenciales y logarítmicas a través de
la revisión de algunos artículos específicos publicados en revistas
especializadas en educación matemática y con ese fin les propone diferentes
preguntas y palabras clave.
Preguntas
como, ¿qué relación existe entre las progresiones geométricas y aritméticas en
la función exponencial?, ¿cómo establecer la relación mayor o menor que, entre
dos potencias indicadas?, ¿existe alguna relación entre la función logarítmica
y la función exponencial?, ¿en qué consiste la escala logarítmica? Llevan a
recoger información de la producción de los estudiantes y a establecer algunos
aspectos de su comprensión.
Se considera
que la siguiente clasificación, que presentamos de la producción escrita de los
estudiantes, entraña una especial riqueza a las reflexiones que los profesores
en formación o en su práctica pueden realizar. Así se examina el concepto
sobre el cual desarrollan su escrito, el registro de representación que
utilizan los estudiantes, el elemento sobre el cual sustentan su escrito -
énfasis – y el uso de las TICS
Concerniente a producción escrita.
Algunos de los aspectos
-considerado es importante resaltar, del escrito que realizan los grupos de los
estudiantes, los presentamos a continuación, retomando partes de
los textos escritos por ellos:
“El diablo ignorándolo le
respondió: Ya que has entendido, comenzaré con el primer paso para poder
graficar la función logarítmica. Para esto, primero debemos hacer lo que
haríamos con cualquier función; tomaremos en cuenta la siguiente ecuación y
realizaremos una tabla de valores, para así saber qué puntos debemos tomar en
cuenta para formar nuestra gráfica, Antes de empezar, debemos tener en cuenta
esta ecuación – El diablo saco de sus bolsillos unas letras y números que
inmediatamente ocuparon un lugar no muy lejano en el espacio y = log2x”.
(Enzenberger, 1998)
-¿Puedes
ver las correspondientes tablas de las ecuaciones?
-Pero
claro que puedo, y antes de que preguntes te voy a responder, observo la
relación inversa de las dos tablas que en la primera ecuación exponencial
convierte valores pequeños, agrandándolos para que la ecuación logarítmica los
transforme en su valor original, tomando valores muy grandes volviéndolos
pequeños; según las ecuaciones, cuando elevamos nuestra base dos a cero, el
resultado será uno, cuando lo hacemos con uno el resultado será dos, y así
sucesivamente, inversamente igual, es bastante fácil de relacionar – Dijo
Robert emocionado, estaba entendiendo todo a la perfección y no podía estar más
agradecido con su amigo Diablo”.(Estudiantes, 2015)
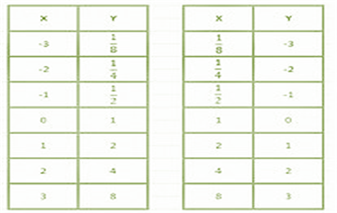
Figura
1. Tabla de valores. Fuente: Autores
Enseguida retoman la
gráfica para las dos tablas de valores (Figura 1). Luego de presentar ejemplos
de la progresión aritmética y geométrica, encontramos:
“El
diablo con una cara de perversión se acerca a Robert y le dice – Bien muchacho,
ahora te voy a poner a prueba ya que entendiste muy bien las progresiones, te
daré una progresión aritmética y una geométrica, tendrás que darme la
explicación de cuál es la relación de estas dos con la función logarítmica – El
diablo hizo aparecer unos números en el viento los cuales se formaron de esta
manera (
Bueno diablo, claramente
las puedo identificar, la primera es una progresión geométrica de razón 2 y la
segunda es una progresión aritmética de diferencia 1. Además,
la progresión aritmética es la sucesión de los exponentes de los términos de la
progresión geométrica, expresados éstos como potencias de 2, lo mostrare
dibujándolo en el suelo – Robert empezó a dibujar con su dedo sobre el suelo,
sus dibujos fueron tomando la siguiente forma:
Luego cada
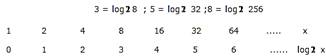
Figura
2. Función – término de progresión geométrica
El
término de la progresión aritmética se obtiene calculando el logaritmo de base
dos, del correspondiente término de la progresión geométrica
En
la observación concerniente al Grupo 5, llama la atención que los estudiantes
escriban:
“En
efecto mi pequeño aprendiz. Si ya sabemos que los números saltarines crecen con
gran rapidez, por el contrario, los números caídos (logaritmos) descienden a
gran velocidad– afirmó el anciano”. (Grupo de estudiantes de primer semestre)
Es de tener en cuenta que
la razón de cambio promedio de esta función nos está mostrando un lento
crecimiento, por lo tanto se considera necesario que el profesor indague sobre
el significado de afirmaciones como la presentada por los estudiantes, en el
párrafo anterior y les permita analizar las dos funciones respecto a su razón
de cambio y la escala logarítmica con números enteros, que parece ser lo
mencionado en la interpretación de los estudiantes.
Se observa a los
estudiantes universitarios imprimirle a la estrategia de trabajo en grupo se
coincide con otros investigadores (Ibarra-Sáiz & Rodriguez, 2007) en que
esta estrategia les permite hacer lo siguiente:
·
abordar
tareas de aprendizaje retadoras
·
debatir
con argumentos y expresar opiniones fundamentadas
·
construir
argumentos sobre la base de las aportaciones de los demás
·
ser
conscientes del valor de las propias aportaciones personales
·
valorar
positivamente las aportaciones de los compañeros
Para el objetivo solo se
toman los segmentos de tal forma que por medio de ellos, habiliten a plantear
reflexiones al profesor, que le permitan hacer uso o re-aprender sus
conocimientos de la enseñanza de las matemáticas (Vargas, En prensa; Oliveira
& de la Roque, 2011).
Algunos de los aspectos
del escrito que realizan los grupos de los estudiantes, se presentan a
continuación, se retoman partes de los textos escritos por estudiantes:
-Ya
sé, vas a enseñarme alguna forma en la que pueda utilizar las funciones
logarítmicas. Dijo Robert.
-Qué
listo eres, así es. Dijo el diablo.
-
¿Sabes cuál es la medida de acidez de un líquido?
-Sí,
es el pH. Responde Robert
-Correcto
está basado en la cantidad de iones de hidrógeno [H+] en el líquido.
La
fórmula del pH es:
pH
=-log [H+]
-Fíjate,
[H+] es la concentración de iones de hidrógeno y está dada en una
unidad llamada mol/l, donde 1 mol equivale a 6,22x1022 moléculas de
átomos.
-Tenemos
en este recipiente jugo de limón, vamos a averiguar cuál es la medida de
acidez.
El
diablo toma dos tiras de papel tornasol y las introduce en el recipiente, en
poco tiempo cambia de color; la azul cambia a rosado y la roja conserva el
color.
-Es
un líquido ácido, pero necesitamos una cifra exacta. Dijo Robert.
-Muy
bien, Robert. Agregó el diablo.
1. ¿Considera que es
correcta la definición de pH presentada en el escrito de los estudiantes
(figura 6), o preferiría revisar ese concepto antes de usarlo en su clase de
matemáticas?
2. ¿Explique cómo y por qué utilizaría usted el pH –
grado de acidez o basicidad de una sustancia - para enseñar la función
logarítmica o a manera de una aplicación de dicha función?
Ahora
el diablo toma un peachimetro y lo introduce en el recipiente, este arroja
1.7, como resultado.- Recuerda que: de 0 a 6 es un ácido, 7 es neutra. De 8 a
14 es básica. La pregunta que tenemos que responder es: ¿cuál es la
concentración de iones de hidrogeno (mol/l) del jugo?
-
¿Cómo puedo hacer esto?, Robert pregunta.
-
Primero se debe sustituir el pH conocido en la fórmula y representa tu
incógnita [H+] con la variable x.
Si
1,7= -log x, entonces log X= -1.7 Resuelve x.pH=-log [H+] 1.7=
-log x -1.7= log x
-
Entonces se utiliza la inversa de logaritmo para despejar a x y ¿Cuál es la
inversa?
-
La exponencial. Contesta Robert.
-
Y así hallamos la respuesta: 10-1.7
-Oh,
gracias, la concentración de iones de hidrogeno en el jugo de limón es de
0.019952623…
3. ¿Qué grado de
comprensión de la función logarítmica, está exhibiendo un estudiante que
solucione este problema, de la manera expuesta en la figura 3?
4. ¿Qué explicación
brindaría usted a un estudiante que pregunte, por qué aplicar el logaritmo a la
concentración de iones hidrogeno, para identificar la acidez, en lugar de usar,
para referirse a la acidez, simplemente el número hallado?
5. ¿Cómo continuaría
usted esta noche, para examinar la razón de cambio promedio, en algunos puntos
de la función logarítmica?
6. Realice un ensayo que
contenga un diálogo, de al menos cuatro intervenciones de dos de los
personajes, explicando la razón de cambio promedio de la función logarítmica.
7. Sea el siguiente
experimento, utilizando un conjunto de sensores y un equipo para recolectar
datos. Utilizando LabQuest*2 para recolectar los datos y un sensor de pH para
líquidos y semisólidos (Flat pH Sensor) del conjunto de Vernier Software &
Tecnology.
El profesor de
matemáticas tiene un acceso limitado a los laboratorios de química y física,
razón por la cual se opta por trabajar con un equipo portátil que incluye dos
Labquest2, un sensor de sonido, uno de temperatura y uno de pH. Es importante
señalar que el laboratorio como tal trae también la posibilidad de medición de
intensidad de la luz. Todos estos fenómenos permiten modelar fenómenos a partir
de funciones logarítmicas.
Es posible tener
comunicación entre los LabQuest*2 y trabajo simultáneo entre los demás
integrantes del equipo desde su celular o tablet; descargado previamente la app
Verinier Graphical Analysis free. También es posible tener acceso a las
pantallas de los dispositivos con el software LabQuest Viwer e interactuar
desde la pantalla de los computadores y descargar el software Logger Lite.
En el caso de la escala
musical el profesor puede entrar a indagar algunas tomas de datos con el uso
del micrófono una vez se haya familiarizado con el conjunto de aparatos que
formaran parte de su laboratorio portátil.
El siguiente es un caso
de pH; en cinco momentos diferentes un jugo de limón que inicialmente tiene un
volumen de 12,5 ml y cuyo pH es 2.80 y vamos en cada evento diferente agregando
12.5ml de agua y realizando una medición del pH de esta mezcla, cuyos datos se
presentan en la siguiente tabla. La gráfica que se obtiene al analizar los
datos de los momentos contra el pH(Tabla2)
Tabla 2. Datos pH
|
Evento
|
pH
|
|
[H*]
|
|
|
1
|
2,79882292
|
|
0,00158919
|
|
|
2
|
2,88941116
|
|
0,00129
|
|
|
3
|
2,9917641
|
|
0,00101914
|
|
|
4
|
3,04529352
|
|
0,00090096
|
|
|
5
|
3,1099994
|
|
0,00077625
|
|
Fuente: Autores
En un
experimento un grupo de profesores ha tomado datos del cambio del pH de una
dilución de limón (Figura ), en la cual se centran en las columnas tituladas
serie dos en las cuales podemos examinar las variables tiempo en segundos y pH.
Se observa que en el intervalo de 0.6 segundos a 0.7 segundos el pH tuvo un
cambio de 2.75 a 2.74. Por lo anterior no se puede concluir que en una décima
de segundos la concentración de iones hidrogeno cambio una centésima. ¿Cuál
sería una conclusión correcta del cambio que sufrió las concentraciones de
iones hidrógeno y cuál el papel del logaritmo en dicha explicación?
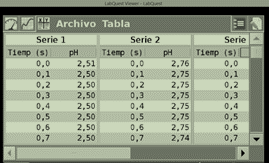
Figura 3 Datos pH.
Fuente: Autores
De igual manera trabajan
con las siguientes inquietudes:
8. ¿Qué diferencia de
concentración de iones hidrogeno existe entre una dilución de pH 3 y una de pH
4? ¿Es la misma diferencia de concentración de iones hidrógeno entre una
dilución de pH3 y pH4 que la que hay entre una dilución con pH entre 5 y 6?,
¿Cuál es el comportamiento de las diferencias?
El caso de la escala musical.
Mirada con énfasis en
la relación entre una progresión aritmética y una geométrica.
Existen estudios de la
función logarítmica que señalan la importancia de comprender está función
vinculada al desarrollo histórico – epistemológico del concepto, además afirman
que en las aulas, la presentación de las funciones logarítmicas, como inversa
de las funciones exponenciales, ha conducido a que se descuiden aspectos que
las dotan de significado, destacando entre ellos la relación entre la
estructura multiplicativa de la variable independiente y la aditiva del
logaritmo (Vargas, J., Pérez, M., González, MT., 2011)
Definiciones de logaritmo
como vínculo entre una progresión aritmética y una geométrica fueron utilizadas
en el siglo XIX. (Serret, 1887), por ejemplo, establecía la siguiente:
I. Dadas dos progresiones crecientes e
indefinidas:
1,
r, r 2, r 3, r 4… (1)
0,
d, 2d, 3d, 4d,… (2)
una por cociente,
comenzando por 1, y la otra con diferencia d comenzando por cero, se llama logaritmos
de los números que forman parte de la progresión por cociente a los números que
le corresponden respectivamente en la progresión por diferencia. Las dos
progresiones, de las cuales se trata constituyen un sistema de logaritmos, sujetas
solamente a la condición de comenzar la primera por 1 y la segunda por 0.
(Serret, 1887, p. 270).
Una representación gráfica
del concepto de logaritmo dado por Serret, en un contexto de geometría
dinámica, se muestra a continuación. Tomemos la progresión geométrica 1, r, r 2,
r 3,… y la aritmética 0, d, 2d, 3d,… en donde diremos, con Serret,
que logaritmo de 1 es 0, logaritmo de r es d, logaritmo de r2 es 2d,
etc. En el eje horizontal colocamos la progresión geométrica y en el vertical
la aritmética (los logaritmos).” (Vargas, J., Pérez, M., González, MT., 2011,
p.132)
Existen otros autores
como López y Ferrari (2007), además de los mencionados en el recuadro anterior,
que describen una construcción de la representación gráfica de la función
logarítmica.
9. Puede usted planear la
lectura de estos dos artículos e intentar realizar las construcciones allí
exhibidas, para luego presentar sus conclusiones, utilizando el software que
sea necesario, en una puesta en común. Si tiene un equipo de profesores. Un
grupo puede realizar la presentación de una construcción y el otro grupo
interrogar sobre los argumentos que la sustentan. Luego el otro grupo pasa a
ser el expositor, con un esquema que aporte en estrategias que inviten a
establecer un diálogo que estimule las habilidades de escuchar las intervenciones
de cada participante.
Escala
Musical – La Octava Musical. No solo las ocho notas musicales se
originan al hacer vibrar una cuerda de distintas longitudes, de igual manera se
pueden construir al dividir en diferentes partes un tubo por el cual circula
aire (Figura 4).
____________________________________ do (Unidad)
________________________________re (8/9)
____________________________ mi (64/81)
__________________________ fa (3/4)
_______________________ sol (2/3)
____________________ la (16/27)
___________________ si (128/243)
__________________ Do (1/2)
Figura 4. División para construir las notas musicales.
Fuente: http://proyecto-artistico.blogspot.com.co
De la figura anterior se
puede extraer la sucesión de las ocho notas (Es usual encontrar el uso de
mayúsculas al escribir las notas musicales (DO RE MI FA SOL LA SI DO), la
diferencia entre el primer Do y el segundo Do es que el último da el inicio de
la siguiente octava) de la escala musical: do re mi fa
sol la si Do. A esta sucesión se le denomina octava musical.
Cada nota tiene su correspondiente octava, más aguda a la derecha (o por
encima) o más grave a la izquierda (o por debajo). Por ejemplo, tomando como
base la nota do central (se le conoce como tónica
por ser la nota base, sin embargo cualquier otra nota puede ser la tónica) su
octava superior es la nota Do (figura 5).
Hoy por hoy las notas
musicales no se definen de acuerdo a la longitud del objeto vibrante, sino a partir
de la frecuencia de vibración de la onda sonora emitida por dicho objeto
(Tomasini, 2007). La ecuación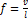 
relaciona la frecuencia f
(medida en hertz) y la longitud de onda 
(medida
en metros), con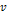 
la velocidad del sonido
medida en metros por segundo. Frecuencias muy altas caracterizan tonos agudos,
frecuencias muy bajas caracterizan tonos graves.
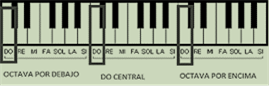
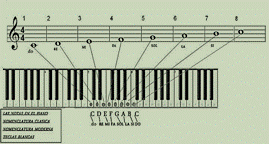
Figura 5. Sucesión octava
musical. Fuente: https://sweepfliping.wordpress.com
Materiales: Sensor
de sonido y LabQuest- Aplicación de celular (Ejemplo: Best Tuner) en caso de no
tener el sensor- Aplicación piano virtual (usar virtualpiano.net). Usando el
sensor de sonido y el LabQuest*2 o la aplicación de celular registre en una
tabla (la cual se llamará Tabla 1) las frecuencias emitidas por las ocho notas
musicales centrales de un piano (figura 5). Se observan las teclas que marcan
las ocho notas musicales centrales, pero surge naturalmente el interrogante ¿Qué
indican las 5 teclas negras que se encuentran entre las teclas blancas que
marcan las ocho notas musicales centrales? Pues bien en el siglo XVIII
Juan Sebastián Bach (1685 - 1750), en su obra “El clave bien temperado” efectuó
algunos cambios fundamentales que habían sido introducidos a la escala musical.
Es a partir de este momento en que la nueva escala llamada temperada es
utilizada en Occidente (Álvarez, 1991). En esta escala existen once frecuencias
intermedias entre una nota y su octava más aguda, estas son: do
do# re re# mi fa fa# sol sol# la la# si Do
Donde el signo #
indica una nota sostenida; en el piano corresponden a las 5 teclas
negras que se encuentran entre las teclas blancas (Figura 5). De lo anterior se
puede concluir que todo el conjunto de notas es una octava y que en el teclado
de un piano se tienen varias octavas (Ver figura 15).
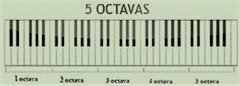
Figura 6. Fuente: http://www.estudiarpiano.com
Construya una segunda
tabla, use las frecuencias de la Tabla 1, agregando las frecuencias de las notas
sostenidas y las frecuencias de las notas que están ubicadas en la cuarta
octava del piano que se muestra en la figura 15. Luego verifique la relación
que define la proporción armónica, para ello elija como tónica otra nota
distinta a do y encuentre el intervalo de cuarta.
El valor de la longitud
del intervalo de cuarta viene dado por el cociente entre las frecuencias de la
tónica y su cuarta. En el caso de la nota do y su cuarta fa se
tiene:
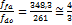(2)
10. ¿Qué relación existe
entre la media aritmética y las notas musicales? Para responder a esta
pregunta es necesario considerar la tabla construida en la primera actividad.
Elija una nota musical y su octava, calcule la media aritmética entre sus
frecuencias. ¿El valor obtenido es aproximadamente la frecuencia de cuál
nota? ¿Qué relación tiene esta última con la tónica elegida?
Si se han resuelto
satisfactoriamente las preguntas antes formuladas es posible que el estudiante
deduzca que la media aritmética establece una relación entre la tónica y su
quinta, esto es lo que se conoce como el intervalo de quinta. El valor de la
longitud del intervalo de quinta se encuentra hallando la razón entre la quinta
y su tónica, por ejemplo, tomando como tónica la nota do, su quinta es
la nota sol; el valor de la longitud del intervalo de quinta es:
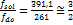(3)
La media armónica de dos
números se define como:
(4)
La proporción armónica
define la relación entre la tónica y su cuarta, por ejemplo, al considerar a
como la frecuencia de la nota do y c como la frecuencia de la Do,
es decir la octava de do se obtiene aproximadamente la frecuencia de la
nota fa, esto se conoce como intervalo de cuarta o cuarta perfecta, así
si elegimos como tónica la nota do la nota con la que cual estaría
relacionada es la nota fa.
11. Construya
una tabla usando las frecuencias de la Tabla 1, agregando las frecuencias de
las notas sostenidas y las frecuencias de las notas que están ubicadas en la
cuarta octava del piano que se muestra en la figura 15. Luego verifique la
relación que define la proporción armónica, para ello elija como tónica otra
nota distinta a do y encuentre el intervalo de cuarta.
El valor de la longitud
del intervalo de cuarta viene dado por el cociente entre las frecuencias de la
tónica y su cuarta. En el caso de la nota do y su cuarta fa obtienen:
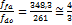(5)
Verifican que la longitud
del intervalo de cuarta no varía al realizar el cociente entre cualquier otra
nota musical y su cuarta. Si se toma las frecuencias de las notas centrales a
= fdo y b = fDo (frecuencias de las
notas do y Do respectivamente ubicadas en la tercera octava de un
piano) se obtiene la frecuencia de la siguiente octava de Do, denotada
por Do4. La media geométrica se expresa entonces como:
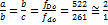(6)
Y definen la relación
entre octavas sucesivas o intervalo de octavas. Verifican al usar las
frecuencias de la tabla, toman como tónica otra nota distinta a do y encuentran
su octava. El valor de la longitud del intervalo de octavas viene dado por el
cociente entre las frecuencias de la tónica y su cuarta, al tomar las
frecuencias de las notas do y su octava Do, se puede encontrar
que el valor de la longitud del intervalo de octava es 2. Lo anterior quiere
decir que la frecuencia de una nota una octava más aguda que otra es
exactamente el doble de esta, así si se tiene un La a una frecuencia de
440 Hz (herz), el siguiente La más agudo (1 octava más arriba) estará
exactamente a una frecuencia de 880 Hz, mientras que el anterior, más grave (1
octava más abajo), estará a la mitad con una frecuencia de 220 Hz. Verifican
que la longitud del intervalo de cuarta no varía al realizar el cociente entre
cualquier otra nota musical y su octava.
Progresión aritmética.
Por ejemplo, la sucesión de números 1, 6, 11, 16, 21… es una progresión cuya
diferencia es 5. Completan la tabla 2 con sus respectivas frecuencias.
Tabla 3. Posición de Notas musicales para analizar
frecuencias
|
Posición
|
Nota musical
|
Frecuencia
|
|
1
|
do2
|
|
|
2
|
do#2/reb2
|
|
|
3
|
re2
|
|
|
4
|
re#2/mib2
|
|
|
5
|
mi2
|
|
Fuente: Autores
12. ¿Según la Tabla 2 en
la columna posición, cómo está relacionados el listado de números que aparecen?
¿De acuerdo a la respuesta obtenida en la pregunta anterior, se puede concluir
lo mismo de la lista de frecuencias? Si la respuesta no es afirmativa ¿cómo
podemos establecer una relación entre los valores de la lista de frecuencias?
Progresión geométrica.
Considérese la nota La a la derecha del do central, la cual tiene
una frecuencia de 440 Hz, el sonido de referencia recomendado
internacionalmente para la afinación de los instrumentos. Además como ya se ha
dicho la relación entre octavas es de 2 a 1, por lo que la diferencia entre el La3
y el La4 es de 220Hz, mientras que entre el La4 y La5 es del
doble, 440Hz. De igual manera, entre La5 y La6 sigue siendo el
doble, 880Hz. Si se representa en un eje de coordenadas la frecuencia de cada
nota musical 14. ¿La representación es lineal?, al reflexionar un poco sobre
esta pregunta la respuesta fue no, aunque sobre el papel si se observe que hay
la misma distancia entre La3 y La4, La4 y La5, ... Construya
una tabla similar a la Tabla 2 que contenga las frecuencias de cada nota
musical entre la 3ra, 4ta y 5ta octava de un piano, incluyendo las notas
sostenidas o bemoles. Luego elabore un gráfico y explore lo comentado en el
párrafo anterior.
Este tipo de series en
las que la linealidad se pierde, pero en las que se determina una proporción
constante es lo que se conoce como una progresión geométrica (Pastor, 2088). Lo
anterior sugiere el uso de los logaritmos para poder representar linealmente
magnitudes que varían exponencialmente. Se deduce entonces que las notas
uniformemente espaciadas a lo largo de un piano es la visión logarítmica de la
progresión geométrica. Pero si esto es cierto entonces debe existir un factor
multiplicativo constante o en otras palabras la razón de la progresión, ¿cuál
es esta razón?
Para dar respuesta al
interrogante primero se debe considerar la definición de progresión geométrica
y relacionarla con la teoría musical descrita a lo largo de este trabajo de
investigación.
Antes de hacerlo cabe
mencionar por ejemplo que la diferencia entre la nota Sol y Sol# es
lo que se conoce como un semitono más alto (o un La bemol, eso se deja a
consideración) igual que en el caso de las notas Fa# (o Sol
bemol) y Sol, las cuales tienen una diferencia de un semitono más
bajo. Lo anterior quiere decir que entre dos notas consecutivas cualesquiera
existe siempre, exactamente, el mismo intervalo. Así, en la escala temperada
dos frecuencias de notas consecutivas verifican la relación:
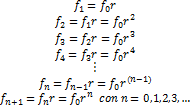(7)
Sorprendentemente las
anteriores igualdades tienen la forma de una progresión geométrica de razón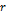 
en
la que el término general caracteriza la relación entre las diferentes
frecuencias de la escala temperada y donde 
indica la frecuencia de
la nota tónica (o nota menor). Un resultado adicional de esta ecuación es que
permite encontrar el valor de la frecuencia de cualquier nota musical de la
escala siempre y cuando se conozca el valor de la razón.
15. ¿Cómo se podría encontrar el valor de la razón? Considere
como tónica la nota La que está a la derecha del do central
(denotada por La4), la cual tiene una frecuencia de 440 Hz. Es claro que
su octava más alta está ubicada a 12 semitonos de ella, esta es la nota La5,
la cual tiene frecuencia
880Hz. Entonces, para
encontrar el valor de la razón considérese la nota siguiente a La un
semitono más alto, es decir, la nota La#4 que tiene por frecuencia:
(8)
A su vez, la frecuencia de la nota siguiente, Si,
es:
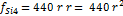(9)
Luego de la nota Si4 empieza la quinta octava
con la nota Do5 con frecuencia:
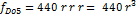(10)
Y así hasta llegar a la nota La5, por lo tanto:
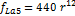(11)
Ya que al repetir el
proceso anterior hemos avanzado doce semitonos y como se conoce además que la
frecuencia de la nota La5 es 880Hz, sustituyendo en la última ecuación y
despejando 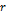se tiene que:
(12)
Teniendo en cuenta lo
anterior, calcule las frecuencias de Re5, Fa#5 y del Do4. ¿Qué pasa en este
último?
Relación entre la
progresión aritmética y la progresión geométrica con la escala musical Al representar dos octavas de un piano en el pentagrama se obtiene
(figura 7)
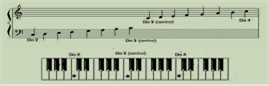
Figura
7. Relación entre las progresiones aritmética y geométrica con la escala
musical
Al
graficar en ejes coordenados las frecuencias de las notas musicales, se obtiene
la figura 7 que los puntos que son de la forma (posición, frecuencia) se
ajustan a la gráfica de una función exponencial. Lo más llamativo de todo esto
es que tomando logaritmos es posible alinear las notas de un modo similar al
que se hace en un pentagrama. La razón principal está en que el pentagrama es
un gráfico logarítmico el cual muestra la diferencia entre los logaritmos de
las frecuencias y no la diferencia entre las frecuencias.
Aunque
dentro de la teoría musical se deben considerar las notas que difieren de medio
tono o de un tono, los sostenidos y bemoles quienes modifican estos saltos de
medio tono arriba, medio tono abajo, entre otros. Lo cual sugiere que el
pentagrama no es una escala logarítmica perfecta pero muy útil para toda
persona interesada en aprender a leer partituras.
Conclusiones
La comprensión de la
función logarítmica que proponemos, a través de su génesis histórica,
concerniente al vínculo entre las progresiones geométrica y aritmética,
aplicado a fenómenos específicos, demanda el estudio sistemático de una red de
conceptos que invita al profesor a profundizar no solo en la matemática sino en
las diversas formas de llegar a comprenderla y el compromiso en las tareas profesionales
de planificación de las clases, la gestión de la discusión en sus clases.
En el ámbito de la
matemática es de gran riqueza integrar el uso de hoja de cálculo dinámica y el
programa geogebra, sin embargo hay que establecer estrategias para que lleguen
al aula. De allí, la decisión de incluir, como ejemplo, las secuencias
elaboradas por los estudiantes, quienes se apoyan en consultas en revistas de didáctica
de la matemática.
El trabajo que se propone
en la hoja de cálculo, inicia en el análisis del comportamiento y de las
regularidades, recurriendo luego al uso del sensor de sonido y el LabQuest*2 o
la aplicación de celular. Esto permite establecer y validar conjeturas, y abre
un campo de oportunidades al docente para explorar diferentes formas de presentar
la escala logarítmica con herramientas cercanas a los estudiantes y en
contextos como la música, resaltar su nexo con las progresiones.
La investigación muestra
ejemplos que coinciden con hallazgos, en estudios que se han llevado a término,
con grupos de estudiantes universitarios, quienes manifiestan un más alto nivel
de implicación cuando se desarrollan las clases en grupos de trabajo
cooperativo y colaborativo.
Referencias
bibliográficas
Alvarez, J. M. (1991).
Matemáticas y Música: El matrimonio secreto. Revista números. 21.
Sevilla.
Blum, W., Galbraith, P.
L., Henn, H.-W., & Niss, M. (Eds.). (2007).
Modelling and aplications in mathematics education.The 14th ICMI Study. New
York: Springer
Enzenberger, H. M.
(1998). El diablo de los números. Madrid, España: Ediciones Siruela
Ferrari, M. (2007).
Construcción social del conocimiento matemático: La función logaritmo. México.:
Departamento de Matemática Eductiva. Memoria Predoctoral. Cinvestav-IPN,
México.
González, S. y Recino, U.
(2013). Las estrategias de aprendizaje en el Educación Médica Superior. Edumecentro,
5(3), 212-224. Recuperado en 11 de febrero de 2017, de
http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S207728742013000300015&lng=es&tlng=es.
González, M. T., &
Vargas, J. (2007). Segmentos de la historia: La función logarítmcia. Matemática:
Enseñanza Universitaria, 129-144.
González, M. T., &
Vargas, J. (2015). Aportes de la historia de la matemática a la investigación
en DMA. En C. Azcárate, & et al, Didáctica del análisis maytemático: una
revisión de las investigaciones sobre su enseñanza y aprendizaje en el contexto
de la SEIEM (págs. 53-63). Santa Cruz de Tenerife, España: Universidad de la
Laguna.
Ibarra-Sáiz, M. S., &
Rodríguez, G. (2007). El trabajo colaborativo en las aulas universitarias:
reflexiones desde la autoevaluación. Revisa de Educación, 369, 355 -
375.
López, R., & Ferrari,
M. (2007). La Función Logaritmo bajo la Perspectiva de la Construcción dada por
Agnesi ( 1748 ). Acta Latinoamericana de Matemática Educativa, 20, 450 -
455.
Maldonado, M. (2007). El
trabajo colaborativo en el aula universitaria. Revista de Educación,
13(23), 263 - 278.
Oliveira, A., & de la
Roque, G. (2011). O potencial das actividades centradas em produçoes de alunos
na formaçao de professores de matemática. RELIME. Revista l. 9(2). 89
Pastor Martín, Angel
(2008). Matemáticas en la música. Revista SUMA. 59, 17-21.
Serret, J. (1887). Traité
d’arithmétique (séptima edición). . París, Francia: Gauthier-Villars.
Sureda, D. P., &
Otero, M. R. (2015). Solving Exponential Situations and
Conceptualization. Educacao Matematica Pesquisa,
17(2), 5 - 28.
Tomasini, M.C. (2007). El
fundamento matemático de la escala musical y sus raíces Pitagóricas,
C&T. Palermo: Universidad de Palermo. 15-27.
Trigueros Gaisman, M.
(2009). El uso de la modelación en la enseñanza de las matemáticas. Innovación
Educativa, Enero-Marzo, 75-87.
Vargas, J. (2017). Investigación
Formativa y Virtualidad. Papel de los docentes universitarios. Nova.
Bogotá: Universidad Colegio Mayor de Cundinamarca.
Vargas, J. (2013).
Análisis de la práctica del docente universitario de precálculo. Estudio de
casos en la enseñanza de las funciones exponenciales. Salamanca, España: Tesis
Doctoral, Universidad de Salamanca.
Vargas, J., &
Gacharná, H. (2008). Capacidad de búsqueda bibliográfica: investigación
formativa con estudiantes de bacteriología y laboratorio Clínico de la
Universidad Colegio Mayor de Cundinamarca. NOVA, 6. 85 - 93.
Vargas, J., Castañeda,
M., & Novoa, J. (2016). Historia y epistemología de la función logarítmica:
conceptualización y marco teórico para la enseñanza del concepto. El caso de la
representación de la curva logarítmica. En Diario de Campo. Bogotá: Universidad
Colegio Mayor de Cundinamarca.
Vargas, J., Pérez, M.,
& González, M. T. (2011). El logaritmo: ¿cómo animar un punto que relacione
una progresión geométrica y una aritmética? En P. P. (Ed.), Memorias del 20o.
Encuentro de Geometría y sus Aplicaciones (págs. 129-138). Bogotá, Colombia:
Universidad Pedagógica Nacional.
Vázquez, V. (1855). Tablas
de logaritmos vulgares desde el 1 hasta el 2000. Madrid : XX Edición..
Villa, J. (2009).
Modelación en educación matemática: una mirada desde los lineamientos y
estándares curriculares colombianos. Revista Virtual Universidad Católica del
Norte. (27), Recuperado de:
http://revistavirtual.ucn.edu.co/index.php/RevistaUCN/article/view/102