Introducción
En el ámbito forense, se afrontan casos singulares que demandan un análisis académico y una exposición pública debido a la complejidad de los fenómenos involucrados. El propósito de tal exhibición es mejorar el proceso de investigación y comprender a fondo cómo ocurrieron los acontecimientos. En este contexto, se presenta un escenario particular que merece atención: la caída de una persona desde varios niveles de altura, durante la cual sus extremidades se enredan con los barandales de un pasillo en el interior de un edificio, hasta que finalmente el cuerpo se precipita hacia el interior de un pasillo superior a la planta baja. Este tipo de suceso podría ser clasificado, según la literatura tradicional, como una precipitación por etapas. Esta clase de caídas han sido escasamente estudiadas, simuladas y presentadas a la comunidad científica.
Desde mediados de los noventa, se utilizan las computadoras para simular caídas (Sloan & Talbott, 1996). Pero no es un área anquilosada. Publicaciones recientes presentan otras propuestas novedosas. Algunas de estas investigaciones utilizan programas comerciales, como se puede encontrar en Yu et al. (2024) y De Vette et al. (2024). Otras, en cambio, optan por desarrollar sus propios modelos numéricos, como en el caso de la representación del maniquí (Pascoletti et al., 2024). No obstante, son escasas las publicaciones que abordan aspectos relacionados con la interacción entre los cuerpos y la arquitectura durante la caída, aunque se pueden mencionar como antecedentes los trabajos de Wach y Unarski (2014) y Muggenthaler et al. (2021).
Las caídas desde grandes alturas tienden a ocurrir con mayor frecuencia en entornos urbanos que en zonas rurales. Esto puede atribuirse al acceso de la población a diferentes niveles en una variedad de edificios. Además, durante procesos de construcción, remodelación o mantenimiento, los trabajadores del ramo están expuestos al riesgo de sufrir caídas.
Desde la perspectiva forense, es fundamental examinar este fenómeno. Según la Organización Mundial de la Salud (OMS), las caídas constituyen la segunda causa de muerte por traumatismos involuntarios; con 684 000 personas fallecidas en el mundo debido a ellas, siendo el 80% de estas muertes en países de ingresos bajos a medianos (Organización Mundial de la Salud, 2021). Las personas mayores de 60 años son el grupo más afectado por las caídas en sus diferentes modalidades.
Además, de acuerdo con la Administración de Seguridad y Salud Ocupacional (Occupational Safety and Health Administration [OSHA]), los trabajadores de la construcción o extracción padecen un alto riesgo de sufrir caídas debido a la falta de equipo de protección y a las condiciones peligrosas en los lugares de trabajo. Estos obreros son otro grupo estadísticamente propenso a sufrir caídas por falta de medidas de protección en obras inacabadas en techos, andenes, escaleras inestables o incompletas, entre otras (Khan et al., 2023).
En Hong Kong, el suicidio mediante salto es frecuente entre la población joven de 15 a 24 años, con tasas del 62.2%, 73.3% y 69.5% en el 2020, 2021 y 2022, respectivamente; siendo este uno de los métodos más utilizados, seguido por el envenenamiento, la suspensión y las quemaduras, entre otros.
Para completar el cuadro, la Fiscalía de Investigación del Delito de Feminicidio de la Ciudad de México afirma que el 20% de los llamados atendidos en el 2023 correspondieron a mujeres que cayeron desde lugares elevados.
La mayoría de los estudios forenses abordan estos casos desde una perspectiva médica, lo que ha sido beneficioso para clasificar las posibles lesiones que pueden ocurrir en diversas alturas y circunstancias. Empero, la contribución desde el punto de vista de los modelos fisicomatemáticos es escasa en la literatura especializada. En este documento, presentamos una perspectiva diferente, utilizando ecuaciones para obtener parámetros físicos y simulaciones numéricas para visualizar posibles hipótesis en un caso particular. La contribución puede ser importante para complementar tanto recreaciones como reconstrucciones de hechos mecánicos de caídas desde diferentes alturas, pero sobre todo para complementar y probar teorías de caso relacionadas con la caída de personas desde grandes alturas.
Fundamentos de caídas
y precipitaciones
En el quehacer forense se considera que cada caso cuenta con particularidades que lo hacen único del resto de las investigaciones del área. Sin embargo, ciertas colecciones de indicios y situaciones permiten que muchos incidentes se clasifiquen dentro de un contexto que facilita su adecuado estudio para esclarecer los hechos.
Por ejemplo, el término ‘caída’ es útil para denominar toda aquella situación en la que una persona pierde súbitamente el equilibrio; la incorregible desviación del centro de gravedad y la falta de un apoyo provocan que el cuerpo se desplace fuera de la normal de su plano de sustentación. A nivel internacional, el verbo ‘caer’ (en inglés: to fall) es la denominación popularmente utilizada para referirse a una gran cantidad de situaciones, más allá de sus singularidades. Tal definición es muy general, incluye a los peatones que resbalan en la acera y terminan su movimiento al nivel del pavimento que anteriormente transitaban, así como al trabajador de la construcción que se encontraba en lo alto de una escalera, hasta que pierde el equilibrio y aterriza de pie en el suelo o bien de la persona que se encontraría atrapada en un edificio incendiándose, y decide que para sobrevivir debe saltar desde una ventana que se encuentra a varios pisos de altura de la superficie. Así, en esta diversidad de situaciones, algunos autores han optado por especificar más el término. Al ser tan general la definición de ‘caída’ se requiere particularizarla. Algunos autores del área médico-legal sugieren la diferenciación entre caída y precipitación: la primera implica que el movimiento termina en el mismo plano de sustentación y que la elevación de donde inicia el movimiento como máximo es igual a la estatura de la persona en cuestión; la segunda, que el plano de sustentación es inferior, pero sin especificar a qué distancia (Ponce, 2021; Vargas, 1999).
En una publicación se propone el uso de la expresión “caída de mediana altura” para alturas comprendidas entre 1.5 m y 10 m, mientras que para alturas superiores a los 10 m se sugiere el término “caída de gran altura” (Campos-Varela et al., 2014). Estas definiciones se fundamentan en un análisis que incluyó nueve observaciones de la caída libre de un maniquí de pruebas en tres posturas diferentes (dos verticales y una horizontal) (Christensen, 2014). Este maniquí se soltó desde alturas aproximadamente iguales, entre 19.81 m y 20.11 m, y adoptó una postura horizontal antes de impactar contra el suelo. Sin embargo, tanto en el estudio original como en investigaciones posteriores que lo referencian, no se proporcionan datos sobre posibles variaciones en función de la altura, modelos biomecánicos que aclaren la dinámica del fenómeno, ni se presentan observaciones adicionales que respalden las definiciones propuestas. Por tanto, se desaconseja utilizar tales definiciones al carecer de sustento verificable suficiente.
Entonces, en la literatura internacional, la caída desde una elevación es una precipitación. Más aún, en algunos textos diferencian la ‘precipitación’ con el término ‘defenestración’, la cual se circunscribe, por algunas publicaciones, en caídas desde alturas con elevaciones entre 10 m a 50 m de altura (Bustos, 2014). Otros textos, más apegados a la raíz etimológica de la palabra (del latín de [‘de, desde’], y fenestra [‘ventana’]) y su contexto histórico (Buzek, 2019), la definen como la proyección desde una ventana o balcón, sin depender de la altura (Villalonga Costa et al., 2015). No obstante, tal término no se relaciona con un fenómeno físico o médico; y hasta asociarlo adecuadamente con alguno, desaconsejamos su utilización.
En tal contexto, más allá de los usos y costumbres en cada demarcación de sistema de justicia, lo mejor es describir a detalle las características de cada incidente, pues las definiciones en la literatura sobre el tema son diversas, ambiguas e incluso contradictorias. En este texto utilizaremos caída y precipitación como expresiones equivalentes.
Física esencial y subclasificaciones del fenómeno
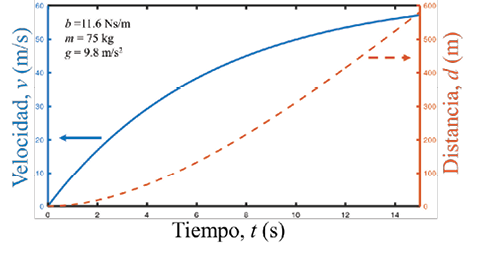
En todos los casos de interés forense, la fuerza gravitacional está involucrada en el fenómeno de caída. Sin embargo, otras fuerzas pueden estar ausentes. Por ejemplo, la fuerza de resistencia del aire que se opone al movimiento del cuerpo rara vez se considera. Como ejemplo, los paracaidistas en caída libre (con el paracaídas cerrado) alcanzan aproximadamente el 95% de la velocidad límite, que es de alrededor de
60 m/s, después de descender 581 m en un tiempo de 15 s (Resnick et al., 2001) (véase Figura 1). En casos donde se considere necesario, la fuerza de arrastre debería aumentar como una función lineal dependiente de la velocidad, sin considerar variaciones de la densidad del aire. Se puede utilizar una ecuación que relacione la velocidad v en función del tiempo t y las constantes de masa m, gravedad g y el coeficiente de fricción del cuerpo b, como puede ser:
 (1)
(1)
Figura 1. Gráficas de la velocidad y distancia que recorre un cuerpo considerando la resistencia del aire
Existen otras fuerzas externas al cuerpo, como las que provocan el inicio del movimiento, como un empujón, un golpe u otro tipo de impulso. Empero, estas solo actúan en el inicio del movimiento del cuerpo que caerá. Una vez que finaliza el contacto entre el cuerpo impulsor y
el cuerpo colisionado, cesa la aceleración externa del cuerpo en caída y estará sujeto a la fuerza de gravedad. La determinación de la existencia de una fuerza externa suele ser decisiva para decidir judicializar un caso. Algunos autores utilizan el término “caída o precipitación acelerada” para referirse a que el inicio de movimiento implicó una fuerza externa, pero es mejor describir que existe una fuerza externa a utilizar una expresión que oscurece el fenómeno técnico que es físico, y que de hecho no se considera una expresión legal.
El cuerpo en caída libre aumenta su velocidad; sin embargo, no es la velocidad la causa de las lesiones, sino la desaceleración al contactar con otro material. Una persona que cae desde una altura de 3 m sobre un colchón de aire inflado sufrirá menos lesiones que si impacta contra el concreto. La velocidad al caer desde 3 m es la misma en ambos casos. De hecho, la velocidad en función de la altura h se puede describir como:
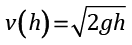 (3)
(3)
Y su tiempo de vuelo tf es descrito por:
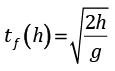 (4)
(4)
Entonces, es el cambio de la velocidad de v(h) el que se relaciona directamente con la producción de alguna herida. Este cambio de la velocidad sucede en un intervalo de tiempo donde interacciona el cuerpo con alguna superficie sólida, el cual puede variar de entre 10 a 36 milisegundos, aunque un valor popular para realizar cálculos es de 15 milisegundos (Milanowicz & Kędzior, 2017; Post et al., 2019).
Entonces, el parámetro físico que produce las lesiones es la aceleración. La producción de lesiones graves se relaciona con aceleraciones intensas y de lesiones leves se relaciona con aceleraciones pequeñas. Estas correspondencias han fomentado definiciones de subclasificaciones de caída y precipitación (Bustos, 2014).
En la literatura médico-legal, las caídas se suelen clasificar en simples, aceleradas, complicadas y post mortem. En las “caídas simples” no se considera alguna fuerza externa al cuerpo que inicie el movimiento de descenso; en las “caídas aceleradas” sí se repara que son el producto de una fuerza que contribuye a que sean más graves las lesiones. No obstante, estas categorías son ambiguas. Puede existir una caída simple con velocidad inicial diferente de cero (0), por desplazamiento de marcha (alrededor de 1.4 m/s); pero también puede existir el caso donde la persona está estática, pero en una posición y postura de equilibrio inestable, como puede ser que la persona tenga una afección motriz, así un pequeño impulso puede ser suficiente para iniciar la caída de la persona.
Las “caídas complicadas” implican que en el movimiento de caída hasta el nivel del plano de sustentación se encontrará el cuerpo con materiales intermedios. Por ejemplo, supongamos que en una oficina una persona se desmaya, en el movimiento su cabeza golpea el borde de una mesa, pero su cuerpo finaliza el descenso al nivel del plano de sustentación, el piso donde originalmente estaba de pie. En estos casos, se pueden identificar fases en el movimiento descendente por acción de las colisiones del cuerpo en determinados objetos que están en el entorno de la persona que cae. En tales situaciones, la caída es coadyuvante de la muerte.
La “caída post mortem” indica que el fallecimiento no es producto de la caída, sino de un agente anterior al movimiento descendente (Salvador Martínez, 2015). Por ejemplo, si una persona de pie recibe un disparo de un arma de fuego en el cráneo, y fallece en ese instante, perderá control de su sistema nervioso central y, por ende, el equilibrio, por lo que caerá. La caída se produce después de la muerte, en un intervalo de tiempo pequeño. También es posible que la persona fuera ejecutada, incluso sin presentarse una caída en el acto, y tiempo después el cuerpo se abandonará en otro lugar, dejándolo caer un par de metros de altura.
Por su parte, las precipitaciones cuentan con la misma clasificación: simple, acelerada, complicada y post mortem. Algunos textos agregan otra categoría: fásica, en la cual se identifican momentos donde el cuerpo impacta otro objeto antes de alcanzar el nivel donde detendrá su movimiento. En tal situación, no difiere la de la precipitación fásica de la complicada.
De este modo, resulta más práctico referirse a estos fenómenos con sus características iniciales: caídas que inician con movimiento o que son estáticas, que se dirigen de manera frontal, lateral o de espaldas, con fuerza externa o sin ella (Bustos, 2014). Además de señalar las fases, se deben considerar los momentos en los que el cuerpo impactó un objeto mientras continuaba su movimiento. Entre los parámetros físicos relevantes se encuentran la altura inicial desde la que comienza el movimiento, la velocidad inicial, la velocidad final, la aceleración de la parte del cuerpo de interés al momento que sucedan impactos con objetos, entre otros, que dependerán más del caso en cuestión.
En tal sentido, en el cuerpo de la víctima, los indicios principales son el tipo de lesiones, la gravedad y la localización, los cuales por medio de un análisis de regresión es probable inferir una altura desde la que inició el movimiento en caída libre (Lau et al., 1988; Milaszkiewicz et al., 2019).
Detalles sobre el caso de enganches
El caso tratado es real. Pero, con el fin de presentarlo ante la comunidad académica a la vez de mantener confidenciales los datos personales de la víctima y familiares, se ha omitido alguna información que permita la identificación de las personas involucradas en el evento. Se han designado algunos elementos de manera aleatoria, como la apariencia de género, color de piel, ropas y paredes y la orientación del norte geográfico. También, se han modificado algunas variables de indicios circunstanciales. Solo se conservan aquellos indicios que criminalística, arquitectónica, biomecánica y físicamente son relevantes. De tal modo que cualquier semejanza con personas vivas o muertas es una coincidencia sin intención.
La situación es la siguiente: se realizó una reunión en uno de los departamentos ubicados en el sexto piso de un edificio que consta de seis niveles y una planta baja. En una vista cenital, el terreno forma un rectángulo, donde la edificación asemeja a una escuadra, con los departamentos en la periferia del rectángulo; cada nivel cuenta con su pasillo y un barandal que separa la edificación del vacío de la construcción, el cual en su planta baja funciona como el estacionamiento del edificio, donde ubicaríamos el centro del rectángulo.
Durante el evento, los asistentes consumieron varias bebidas alcohólicas. En algún momento, notaron la ausencia de uno de los invitados, quien fue visto por última vez afuera del departamento, en el pasillo del sexto piso. Más tarde, se descubrió su cuerpo en el pasillo del primer piso, donde se encontró un lago hemático, sin evidencia de arrastre o traslado del cuerpo. Los zapatos de la víctima se encontraron en el cuarto piso y en la planta baja, respectivamente. No se cuenta con grabaciones de video ni testimoniales que puedan proporcionar información sobre el acontecimiento concreto. De hecho, no hay reportes de escuchar un grito o un golpe fuerte que se relacione con el incidente.
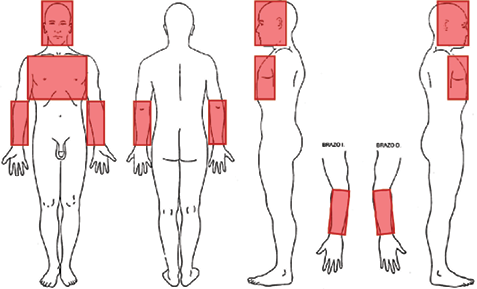
Las lesiones que presenta el cuerpo se ilustran en la Figura 2; las fracturas, golpes contusos y escoriaciones principalmente se encuentran en el rostro, pecho y ambos antebrazos.
Una hipótesis del caso sugiere que, por el consumo de alcohol y por problemas de depresión, la persona, al encontrase sola en el pasillo, se impulsó por sí misma hacia el vacío. Sin embargo, durante la precipitación, sus extremidades contactaron en varios momentos los barandales de diferentes pisos. En uno de esos contactos, una extremidad se enganchó con un barandal produciendo un movimiento de bamboleo, sin alcanzar a formar una oscilación completa, y al desengancharse la extremidad el cuerpo terminó impactando en el pasillo del primer piso. Este tipo de mecánicas de hechos es poco usual.
Figura 2. Esquema anatómico de la localización de las principales lesiones del cuerpo. El esquema está basado en la recomendación del Convenio de Estambul (Villanueva, 2018)
La descripción de cómo pudieron suceder los hechos requiere algún tipo de reconstrucción. La utilización de voluntarios para repetir fases no es viable por cuestiones de seguridad de los participantes; el uso de partes parciales o completas de animales muertos o cadáveres presenta riesgos sanitarios y logísticos para cada intento, por lo cual también se descartó como medio de investigación. La realización de una animación no es confiable, pues no representaría una trayectoria que describa el fenómeno, más bien solo ilustraría posibles momentos. Entonces, una solución es utilizar una simulación numérica y representarla visualmente en la pantalla de un dispositivo digital. La simulación requiere que se encuentren las condiciones iniciales de velocidad y ángulo de lanzamiento, de modo que la computadora reproduzca los indicios de las fases, donde una extremidad contacte un punto del barandal. Sin elementos adicionales, que se cause el efecto de columpio que permita al cuerpo introducirse en el pasillo del primer piso y que ahí termine el movimiento del cuerpo. Tal exploración requiere la contrastación con otras teorías de caso, pero en este documento solo se expone la hipótesis de un salto.
En este caso, las fórmulas analíticas son de poca utilidad. Tales ecuaciones suelen ser para describir el movimiento de una partícula puntual; para el cuerpo humano se idealiza que es el centro de masa. Sin embargo, de existir colisiones entre los barandales y las extremidades es de alta especulación (al momento de estado de la técnica) asignar valores de pérdida de energía cinética mediante el uso del coeficiente de restitución. La mejor solución son los cálculos numéricos y que los resultados se desplieguen en una pantalla.
Metodología: componentes virtuales de la reconstrucción
La programación del modelo virtual se realizó utilizando el software Virtual Crash 3. Este programa se ha empleado en diversas reconstrucciones virtuales de interés forense, muchas de ellas documentadas en la literatura académica y especializada (Becker, 2016; Piantini, 2013; Virtual Crash, s.f.). A continuación, se detallan los elementos incorporados en la reconstrucción siguiendo el modelo metodológico sugerido por Torres-Zúñiga (2022).
Elementos del edificio virtual
Utilizando mediciones del lugar de investigación, datos de la inspección, fotografías y la información contenida en la carpeta de investigación, se programó un modelo tridimensional y virtual del inmueble con el software. Se construyó una escuadra digital usando paralelepípedos con dimensiones específicas: una altura de 3 m, un fondo de 2 m y largos de 6 m y 8 m, respectivamente, como se muestra en las Figuras 3, 4 y 5. Estas escuadras se duplicaron y apilaron para representar un edificio con planta baja y seis pisos.
En el lado norte de la escuadra, cada piso cuenta con un letrero que indica su nivel y una imagen de un ventanal. En el lado oriente, cada piso tiene una imagen de una ventana y en su extremo sur, una imagen de una puerta. En la planta baja del mismo lado, se indica una puerta negra mediante una imagen.
Además, cada piso de la maqueta cuenta con un pasillo de 2 m de ancho y 0.5 m de alto, junto con un barandal de 0.96 m de altura. Este barandal está compuesto por ocho elementos horizontales (seis cilíndricos y uno paralelepípedo en la parte superior) y dos elementos cilíndricos verticales igualmente espaciados, como se ilustra en la Figura 5.
Figura 3. Vistas del escenario digital; a la izquierda: ligeramente de frente, hacia el ángulo de la escuadra que forma la edificación, y a la derecha: de arriba hacia abajo
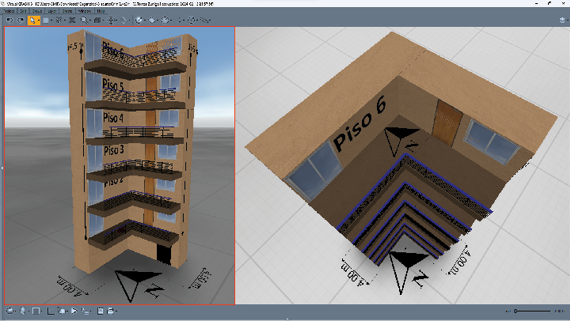
Figura 4. Vistas semilaterales derecha e izquierda, donde se aprecian los elementos arquitectónicos

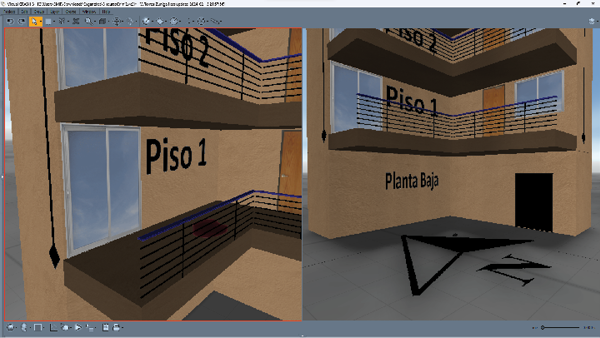
Figura 5. Acercamiento al piso 1 y a la planta baja del escenario virtual. Se pueden observar los elementos criminalísticos del norte en la planta baja y un lago hemático en el piso 1
Elementos criminalísticos
En los costados de las caras de la escuadra, se han colocado indicadores a una altura de 16.5 m, correspondiente a la distancia entre el nivel del primer piso y el centro de masa del maniquí virtual en el momento de iniciar la caída. En la planta baja, se ha incluido una imagen del norte geográfico junto con un modelo de calzado. En el primer piso, cerca de la ventana en el lado de la pared noroeste, se ha incorporado la imagen de un charco de sangre sin indicaciones de arrastre, como se muestra en el panel izquierdo de la Figura 5. En el cuarto piso, se ha ubicado otro modelo de calzado. Finalmente, en el sexto piso, se han instalado nuevamente el norte geográfico y un maniquí, como se muestra en la Figura 6.
Figura 6
Captura de pantalla con dos vistas de la simulación a t = 0.088 s. Inicia el movimiento del maniquí virtual desde su posición y postura inicial

Maniquí virtual
El maniquí se colocó inicialmente en el sexto piso. El modelo virtual del maniquí tiene una altura de 1.580 m y una masa de 54.600 kg. Su apariencia predeterminada por el software no afectó la simulación numérica, evitando así influencias externas en los resultados. No se incluyeron más personajes digitales en la escena. Se establecieron datos iniciales para el maniquí, incluyendo su postura y velocidad inicial. Al comenzar la simulación, el ordenador calcula y muestra en pantalla el movimiento del maniquí hasta que alcanza el equilibrio mecánico, es decir, el reposo.
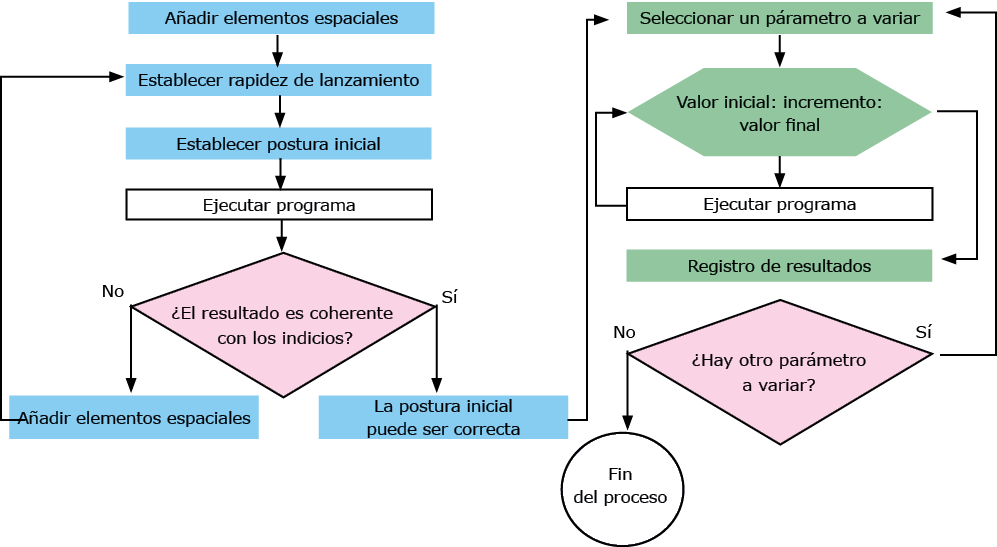
La Figura 7 resume el proceso de construcción, ejecución y evaluación de las simulaciones. Primero, después de construir el escenario, se definen las condiciones iniciales y se ejecuta la simulación. Luego, los resultados se evalúan en función de los indicios disponibles. Si no hay correspondencia entre la simulación y los indicios, se prueban otras condiciones iniciales. Si se encuentra una simulación adecuada, se estudia su estabilidad haciendo pequeñas variaciones en los parámetros seleccionados para determinar el intervalo en el que la simulación sigue siendo similar. Cuando estos intervalos son amplios, la simulación es más confiable, ya que pequeños cambios no provocan resultados drásticamente diferentes.
Figura 7. Diagrama de flujo simplificado del proceso para simular la precipitación y evaluar la robustez de la postura final utilizando los datos de entrada de la postura inicial

Fuente: elaboración propia, basado en Torres-Zúñiga (2022).
Condiciones iniciales del maniquí
y resultados
Se estudiaron los resultados de más de 3500 posturas, pues al cambiar un ángulo o una coordenada en cualquier articulación del maniquí, implica una postura diferente. Además, se varió la magnitud y dirección del vector de velocidad. El cambio de un parámetro, la obtención del resultado y su evaluación tardan aproximadamente un (1) minuto en una computadora estándar.
Después de definir una postura y su vector de velocidad, la computadora inicia los cálculos relacionados con la trayectoria e impactos. Al finalizar cada simulación, se evalúan los resultados. Si lo observado en la simulación es incoherente con los indicios documentados, se hacen cambios grandes a los datos de entrada. Si los resultados son coherentes con los indicios, los cambios son minúsculos pero necesarios para explorar la estabilidad de la respuesta. Este proceso permite converger en una postura y condiciones iniciales cuyos resultados sean semejantes a los indicios. La Figura 6 muestra la postura y posición inicial del caso en cuestión. En este documento se reporta una sola postura: la que mostró los efectos de enganches y es coherente con la documentación de indicios.
Después de iniciar su movimiento, el maniquí se desliza sobre el barandal del piso 6, gira y comienza su descenso de cabeza (véase Figura 8). Debido al deslizamiento, el maniquí gira durante una caída libre que culmina al impactar su pecho y extremidades superiores sobre el barandal del piso 3 (véase Figura 9). Después de la colisión, el maniquí continúa su descenso (véase Figura 10). La cabeza impacta en la parte superior del barandal del piso 2 (véase Figura 11), donde su brazo izquierdo se engancha con una parte del barandal, lo que provoca que el cuerpo oscile hacia adentro del pasillo del piso 1 (véase Figura 12). El maniquí se suelta y termina depositado sobre el pasillo 1, como muestra la Figura 13. La Figura 14 es un resumen de las etapas en las que el maniquí contactó diferentes partes del edificio. En un tiempo neto de 9 s de simulación, el cuerpo muestra los lugares donde se pudieron producir las lesiones exhibidas en la Figura 2. La dinámica del movimiento se puede observar en un video silente (2:17 min) disponible en la dirección electrónica: https://www.youtube.com/watch?v=pG4THp4hiF0
Figura 8. Captura de pantalla con dos vistas de la simulación a
t = 3.200 s. Después de un deslizamiento en el barandal, el maniquí girado cae al vacío. En caída libre gira una vez más antes de impactar contra otro barandal

Figura 9
Captura de pantalla con dos vistas de la simulación a
t = 4.750 s. Uno de los impactos más intensos del pecho del maniquí es contra el barandal del tercer piso
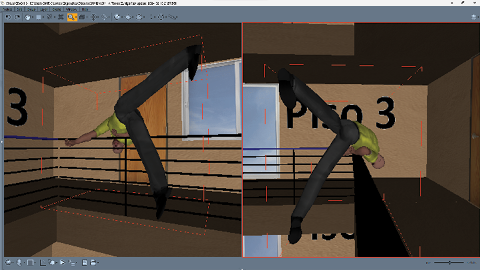
Figura 10. Captura de pantalla con dos vistas de la simulación a t = 5.200 s. Después del impacto en el barandal del tercer piso, el maniquí continúa su caída en dirección al barandal del segundo piso
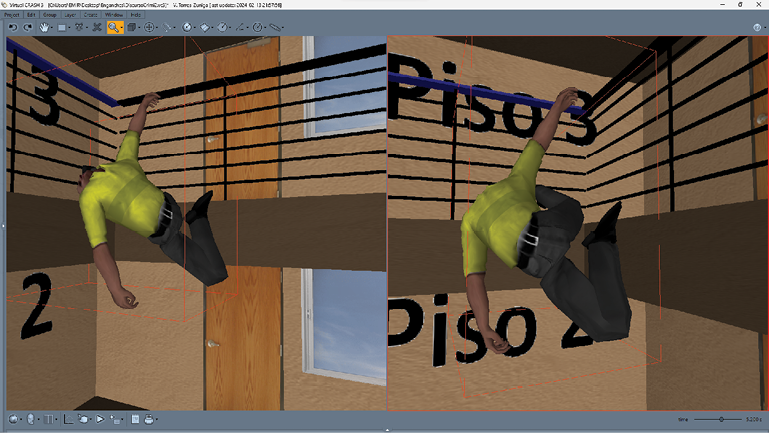
Figura 11. Captura de pantalla con dos vistas de la simulación a t = 5.550 s. En el barandal del segundo piso impacta la cabeza del maniquí
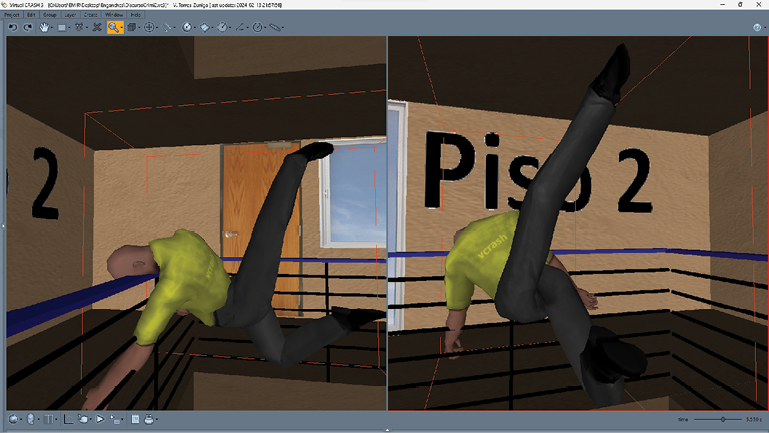
Figura 12. Captura de pantalla con dos vistas de la simulación a t = 6.000 s. En una parte del barandal del segundo piso uno de los brazos se engancha, produciendo un bamboleo en el descenso del maniquí. En la oscilación, el brazo se desengancha y el cuerpo ingresa al pasillo del primer piso
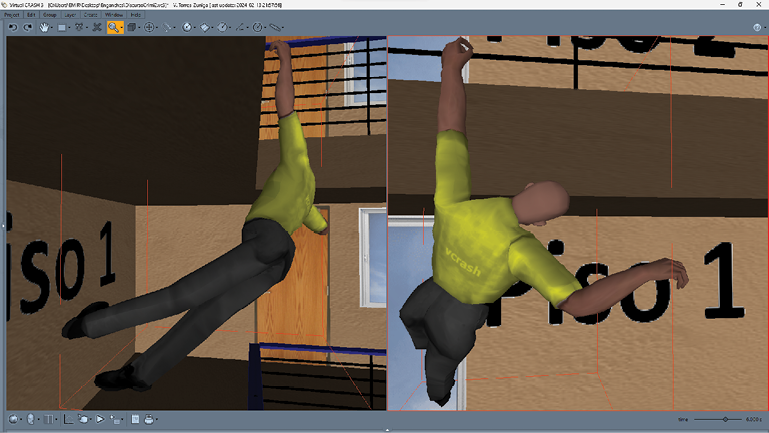
Figura 13. Captura de pantalla con dos vistas de la simulación a t = 9.000 s. En el suelo del pasillo del primer piso es donde se encuentra el cuerpo en su postura y posición final

Figura 14. Dos vistas generales donde se marcan fases de la precipitación, desde la postura y localización inicial hasta la final

Valores cuantitativos de parámetros físicos
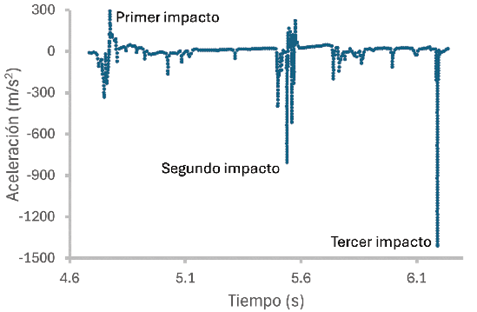
Al tratarse de una simulación numérica, se pueden extraer del programa las magnitudes de parámetros físicos, como la distancia, la velocidad y la aceleración. De las animaciones comunes es imposible obtener tales valores, pues su construcción no implica que sigan con fidelidad las ecuaciones que gobiernan la naturaleza de los cuerpos al caer o colisionar. En la Figura 15 se muestran las gráficas de la velocidad y distancia recorrida por el centro de masa del maniquí. La distancia recorrida no se puede modelar como una parábola, pues no se trata de una caída libre. De hecho, muestra variaciones de tendencia como resultado de las colisiones y los cambios de velocidad. Por su parte, los picos de velocidad son los que asocian a los impactos y aceleraciones que provocan las lesiones. En la región de la cabeza, las aceleraciones alcanzan intensidades netas de 640, 1058 y 1432 m/s2
en intervalos de tiempo de 0.025, 0.035 y
0.009s, respectivamente (véanse Tabla 1 y Figura 16). Estas aceleraciones son muy intensas y se desarrollan en lapsos cortos, por lo que se deben asociar a la producción de las lesiones, como las fracturas.
Tabla 1. Valores de la aceleración de la cabeza en tres impactos del maniquí contra la estructura del edificio
|
Número de impacto |
Primero |
Segundo |
Tercero |
|||
|
Forma del segmento |
Senoidal |
Senoidal |
Pico |
|||
|
Inicial |
Final |
Inicial |
Final |
Inicial |
Final |
|
|
Aceleración (m/s2) |
-340 |
300 |
-820 |
238 |
-1432 |
|
|
Tiempo (s) |
4.750 |
4.775 |
5.540 |
5.575 |
6.185 |
619.4 |
Figura 15
Gráficas de la velocidad y distancia recorrida por el centro de masa del maniquí virtual en la precipitación simulada numéricamente
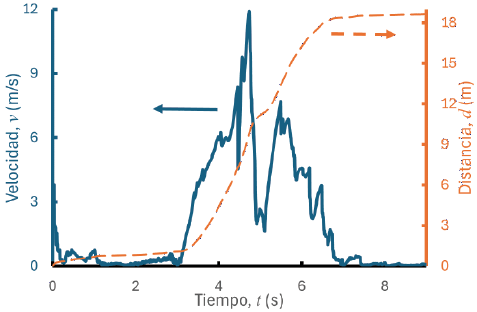
Figura 16. Gráficas de la aceleración de la cabeza del maniquí en función del tiempo. Se muestra solo el segmento de los impactos principales de la simulación
Cotejo entre la simulación y ecuaciones físicas
Con el propósito de verificar la validez de los resultados simulados, se realizó una comparación directa entre los resultados numéricos del software y los teóricos de la caída libre de una esfera en un intervalo de 1 m a 50 m, con incrementos de 1 m. La esfera se definió con un radio de 0.050 m y partió del reposo. Los resultados de las ecuaciones (2) y (3) se compararon uno a uno con los resultados de las simulaciones. Para la aceleración en el momento del impacto entre la esfera y el suelo, se consideró un tiempo de interacción de 0.00529 s, asumiendo una aceleración gravitatoria de g = 9.81 m/s2.
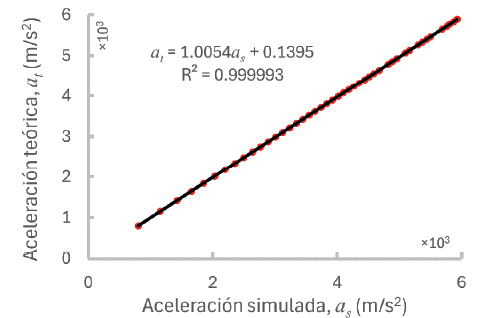
Se elaboraron las gráficas de la velocidad (véase Figura 17), el tiempo de vuelo (véase Figura 18) y la aceleración (véase Figura 19). La tendencia de los datos fue apropiada para realizar un ajuste lineal por el método de mínimos cuadrados y obtener tres parámetros relevantes para evaluar la concordancia entre los conjuntos de datos: la correlación, la pendiente y la intercepción con el eje de las ordenadas. El valor óptimo para los dos primeros índices es 1, mientras que para la intercepción es 0. R2 se puede interpretar como un índice de la idoneidad del ajuste. Mientras que la cercanía de la pendiente al valor de 1 y la intercepción con el eje de ordenadas 0 implican la similitud sistemática en la comparación (Noda, 2005).
La Tabla 2 resume los cálculos. Se destaca una correlación excelente entre los datos, con un mínimo de 99.9993%. La diferencia máxima entre la pendiente y el valor ideal es de 0.0054, considerada adecuada. Respecto a la intercepción, se requiere una operación adicional para su interpretación correcta. Se multiplica su valor por 100 y se divide por el parámetro correspondiente a la altura más pequeña, ya que esta altura implica la mayor incertidumbre entre los datos. En el peor caso, se obtiene una incertidumbre porcentual de 0.06%. Estos valores demuestran la coherencia entre la simulación y el modelo teórico de la caída libre. Por los objetivos de esta comunicación, se considera que los estudios estadísticos adicionales sobre esta coherencia son innecesarios en este momento.
Finalmente, respecto a la estabilidad de la simulación, se observa que un pequeño cambio de cualquier parámetro, ya sea de la velocidad o un ángulo de la extremidad superior, provoca variaciones significativas en los resultados. Por lo general, el maniquí cae en la planta baja. Conseguir que el maniquí ingrese a un pasillo inferior del sexto piso requirió numerosos intentos. Entonces, se debe considerar que la simulación es inestable. Esto es una característica, no un argumento para invalidar la recreación o la hipótesis del caso.
Tabla 2. Valores de correlación, la diferencia absoluta entre la pendiente y el valor ideal, la intercepción del ajuste a línea recta, y la comparación porcentual de los resultados de la simulación contra los resultados teóricos
|
Para la velocidad |
Para el tiempo de vuelo |
Para la aceleración |
|
|
Correlación R2 |
0.999995 |
0.999997 |
0.999993 |
|
|1- Pendiente| |
0.0004 |
0.0002 |
0.0054 |
|
Intercepción |
0.0093 km/h |
0.0003 s |
0.1395 m/s2 |
|
Inct. % a 1 m de altura |
0.06 |
0.06 |
0.02 |
Figura 17. Gráfica del cotejo de los resultados simulados y teóricos de la velocidad de una esfera de prueba. Se observa alta coherencia entre los dos conjuntos de datos
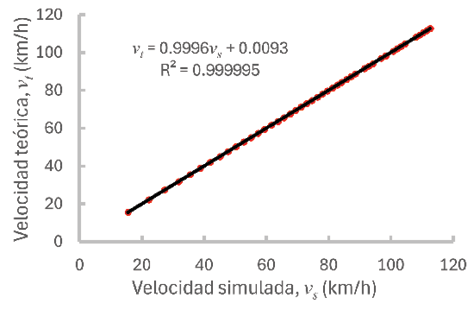
Figura 18. Gráfica del cotejo de los resultados simulados y teóricos del tiempo de vuelo de una esfera de prueba. Se observa alta coherencia entre los dos conjuntos de datos

Figura 19. Gráfica del cotejo de los resultados simulados y teóricos de la aceleración de una esfera de prueba al impactar en el suelo virtual. Se observa alta coherencia entre los dos conjuntos de datos
Conclusiones
Se ha expuesto una revisión de la importancia del estudio de las precipitaciones o caídas de personas desde grandes alturas en el marco de la investigación de casos forenses. En particular, desde la perspectiva de la física se deben conceptualizar estos incidentes desde el contexto materialista de los indicios. Es decir, restringirlos a los conceptos de la física mecánica de los objetos en movimiento o bien explicar a detalle las bases de los conceptos que se desea implicar. Así, expresiones como “defenestración” deben evitarse como recurso fenomenológico. Lo que también aplica para “precipitación acelerada”, pues no se refiere en sí mismo a que el inicio del descenso haya sido causado por una fuerza externa al individuo.
En los casos de “caída libre”, el movimiento del centro de masa de las personas se puede analizar con las ecuaciones que describen a una partícula de la mecánica clásica, ecuaciones que se consideran básicas en los campos de la física y la ingeniería. Empero, cuando el individuo presenta colisiones entre el inicio hasta el final del movimiento, lo mejor es considerarlo como un cuerpo extendido. En estos escenarios, se pueden realizar simulaciones numéricas utilizando computadoras para evaluar hipótesis sobre cómo se desarrollaron los hechos.
Aquí se presenta un caso de precipitación por fases, en el que un maniquí virtual se engancha entre los barandales de un edificio recreado digitalmente. Las simulaciones de prueba muestran una alta coherencia con la física básica que describe a la partícula, lo que brinda confianza en el programa utilizado. Por su parte, las recreaciones del movimiento del maniquí muestran una relación con la producción de indicios, y sus resultados numéricos de desplazamiento, velocidad y aceleración son consistentes con la producción de hematomas y fracturas.
Se requiere más investigación sobre la validación de estos métodos, que implican una convergencia entre las ciencias de la computación, la arquitectura, la ingeniería, la física y la medicina en torno a un tema de criminalística como es la recreación de hechos mecánicos de personas que caen de grandes alturas. Futuros trabajos deben analizar la respuesta de los maniquís precipitados al impactar contra superficies deformables o desplazables, que pueden representar láminas metálicas o volúmenes de agua. Esperamos que este tipo de investigaciones permitan complementar las recreaciones de casos equivalentes, pues la simulación por ordenador de la mecánica de caídas es una herramienta viable para obtener datos significativos en casos forenses.
Agradecimiento
El autor agradece el apoyo al programa CATIC 2023 y 2024.
Referencias
Becker, T. R. (2016). Simulations of pedestrian impact collisions with virtual CRASH 3 and comparisons with IPTM staged tests. https://arxiv.org/abs/1512.00790
Bustos, C. A. (2014). Aspectos forenses de las caídas de altura. Cuadernos de Medicina Forense Argentina, 4(1), 19.
Buzek, V. (2019). La defenestración de Praga. Desperta Ferro: Historia moderna, 40, 14-18.
Campos-Varela, I., Hernández, J., & Rodríguez-Téllez, N. (2014). Caídas. En N. Rodríguez-Téllez, Patología forense, un enfoque centrado en derechos humanos (vol. II, pp. 173-197). Universidad Nacional de Colombia.
Christensen, A. M. (2014). The influence of behavior on freefall injury patterns: Possible implications for forensic anthropological investigations. Journal of Forensic Sciences, 49(1), 5-10. https://doi.org/10.1520/jfs2003089
De Vette, V., Hutchinson, K., Mugge, W., Loeve, A., & Van Zandwijk, J. P. (2024). Applicability of the Madymo Pedestrian Model for forensic fall analysis. Forensic Science International, 361, 112068. https://doi.org/10.1016/j.forsciint.2024.112068
Khan, M., Nnaji, C., Khan, M. S., Ibrahim, A., & Lee, D. C. (2023). Risk factors and emerging technologies for preventing falls from heights at construction sites. Automation in Construction, 153, 104955. https://doi.org/10.1016/j.autcon.2023.104955
Lau, G., Ooi, P. L., & Phoon, B. (1998). Fatal falls from a height: The use of mathematical models to estimate the height of fall from the injuries sustained. Forensic Science International, 93(1), 33–44. https://doi.org/10.1016/s0379-0738(98)00027-9
Milanowicz, M., & Kędzior, K. (2017). Active numerical model of human body for reconstruction of falls from height. Forensic Science International, 270, 223-231. https://doi.org/10.1016/j.forsciint.2016.10.009
Milaszkiewicz, A., Cywka, T., & Teresiński, G. (2019). Verification of usefulness of the method for determining the height of fatal falls proposed by Lau et al. Archives of Forensic Medicine and Criminology, 69(3), 93–99. https://doi.org/10.5114/amsik.2019.94226
Muggenthaler, H., Hubig, M., Meierhofer, A., & Mall, G. (2021). Slip and tilt: Modeling falls over railings. International Journal of Legal Medicine, 135(1), 245-251. https://doi.org/10.1007/s00414-020-02432-8
Noda, B. (2005). Introducción al análisis gráfico de datos experimentales (2ª ed.). Universidad Nacional Autónoma de México.
Organización Mundial de la Salud. (2021, abril 29). Caídas. (OMS). https://www.who.int/es/news-room/fact-sheets/detail/falls
Pascoletti, G., Huysmans, T., Molenbroek, J. F. M., & Zanetti, E. M. (2023). From an ellipsoid-based to an anthropomorphic articulated total body model for multibody applications. International Journal on Interactive Design and Manufacturing (IJIDeM), 18(8), 5991–6011. https://doi.org/10.1007/s12008-023-01427-0
Piantini, S. G. (2013). Advanced accident research system based on a medical and engineering data in the metropolitan area of Florence. BMC Emergency Medicine, 13(3), 1-18. https://doi.org/10.1186/1471-227x-13-3
Post, A., Taylor, K., Hoshizaki, T. B., Brien, S., Cusimano, M. D., & Marshall, S. (2019). A biomechanical analysis of traumatic brain injury for slips and falls from height. Trauma, 21(1), 27-34. https://doi.org/10.1177/1460408617721564
Resnick, R., Halliday, D., & Krane, K. S. (2001). Física. Compañía Editorial Continental.
Salvador Martínez, M. C. (2015). Caída de altura: estudio en el cadáver de los diferentes cuadros de fracturas óseas y los factores que intervienen en su producción. Importancia de la evaluación radioscópica [Tesis de Doctorado, Universitat de Valencia]. Repositori d'Objectes Digitals per a l'Ensenyament la Recerca i la Cultura (RODERIC).
Sloan, G. D., & Talbott, J. A. (1996). Forensic application of computer simulation of falls. Journal of Forensic Sciences, 41(5), 782-785. https://doi.org/10.1520/JFS13997J
Torres-Zúñiga, V. (2022). Comparación analítica entre video y simulación de una precipitación. ReCiF, 1(1), 23-37.
Vargas, E. (1999). Medicina legal (2ª ed.). Trillas.
Villalonga Costa, L., Bayona Santana, D. R., & Estupiñán Rodríguez, N. (2015). Defenestración. Presentación de un caso. Revista Médica Electrónica, 37(3), 272-278. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1684-18242015000300009
Villarreal Ponce, N. C. (2021). Precipitación vs caída: valoración médico forense como causa de muerte. The Ecuador Journal of Medicine, 1(Esp), 76–88. https://doi.org/10.46721/tejom-vol1issesp-2021-76-88
Villanueva, C. R. (Ed.). (2018). Manual para la investigación y documentación eficaces en la tortura y otros tratos o penas crueles, inhumano o degradantes. Comisión Nacional de los Derechos Humanos.
Virtual Crash. (s.f.). Validation & Study. Validation and study of Virtual Crash. Virtual Crash. https://www.vcrashusa.com/vc-validation-vc
Wach, W., & Unarski, J. (2014). Fall from height in a stairwell–mechanics and simulation analysis. Forensic Science International, 244, 136-151. https://doi.org/10.1016/j.forsciint.2014.08.018
Yu, X., Baker, C. E., & Ghajari, M. (2024). Head impact location, speed and angle from falls and trips in the workplace. Annals of Biomedical Engineering, 52, 2687-2702. https://doi.org/10.1007/s10439-023-03146-9