Introducción

En el universo de las relaciones humanas se han establecido categorías de observación, con las cuales se establece conciencia de la dualidad de la existencia; la existencia real de los elementos y la existencia ideal de estos; la categoría que señala los elementos u objetos como de existencia real versa su visión sobre las relaciones sensibles y las perceptibles; en las sensibles intervienen los sentidos: vista, tacto, gusto, oído, olfato y una que establece relaciones entre los espacios, el tiempo y otros múltiples factores que intervienen en una generación de causa efecto (intuición). Las perceptibles se pueden señalar como las establecidas entre el sujeto y el objeto en una interrelación tal que provoca una descripción mediatizada por los sentidos e instaurada como imagen cognitiva del elemento u objeto real en los esquemas mentales de quien lo percibe como tal desde una reflexión:

En virtud de lo enunciado, para la filosofía analítica el papel y el propósito de la reflexión es hacer claras, mediante el análisis, las proposiciones para profundizar en los fundamentos …Su objeto –según Kaplan- es poner al descubierto los átomos lógicos de lo que están compuestas nuestras ideas complejas. (SolanoJ, p.140)

En el desarrollo del pensamiento matemático desde lo educativo, la acción curricular debe generar en el maestro la conciencia de las relaciones existentes que él puede resaltar,

(…)al establecer el plan de un conjunto de experiencias matemáticas, puede ocurrir que una experiencia determinada afecte al estudio de otros conceptos en varias ramas muy distintas de las matemáticas, y que estos efectos no sean observables hasta mucho después, quizás hasta años más tarde. (Dienes, Z. P, 1970, p.18)

Es así como el individuo puede desarrollar la construcción de sus percepciones y las formas, como sus ideales pueden generar visiones simples de una realidad compleja, al restringir el marco referencial en la construcción y el desarrollo de una aplicación establecida desde un proceso histórico cultural llamado educación matemática, que proporciona medios para desarrollar relaciones que establecen regularidades sobre las percepciones y produce elementos abstractos con los cuales visiona otras regularidades, que interpretado desde los símbolos culturales establecidos en el devenir histórico de la teoría, se han erigido como objetos matemáticos.

Justificación

Reconocer el entorno como relaciones en permanente construcción de objetos matemáticos desde las idealizaciones tales que permiten la generación de reglas de comparación, con las cuales se hace factible la generación de un quantum o valor que hace posible la modelación de los fenómenos reales o imaginarios, desde el marco referencial construido e idealizado para favorecer su socialización, justifican el presente proyecto de investigación, de allí que la educación matemática debe ocuparse de la didáctica, que haga factible establecerla como una relación individual y colectiva entre el sujeto que sabe y su grupo social que mediatiza el conocimiento, bajo las dinámicas de acciones de construcción (armar) y deconstrucción (desarmar) en la que cada integrante de la comunidad construye su marco referencial o asume una posición que le permite ingresar paulatinamente a los constructos colectivos de los objetos matemáticos, en la búsqueda de lo simple para armar y desarmar lo complejo.

Ellos son modelos construidos desde una intencionalidad individual y colectiva que hace posible la permanente transformación.

Según plantea un autor:

En lo referente al modo en que los distintos diseños y morfologías que observamos en nuestro alrededor han llegado a surgir, podemos aceptar sin mayores dificultades la idea fundamental de la teoría evolucionista, según la cual todo se desarrolla o evoluciona hasta alcanzar formas cada vez más adaptadas a su entorno.( Stevens P, 1987, p. 41)

Estos modelos se interiorizan en el individuo, quien construye formas de interactuar, demostrar y argumentar, con lo cual aparece necesariamente la construcción y deconstrucción de acciones que llevan a los espacios lógicos de verdad y los procesos matemáticos, desde la idealización de los fenómenos.

Desarrollo Teórico

Las operaciones matemáticas no escapan de las acciones de construcción y deconstrucción, sino que además dan cuenta de las propiedades o raíces de los objetos construidos dentro de las necesidades culturales del hombre, de allí que estos objetos matemáticos traducidos a acciones y propiedades necesiten de la didáctica que permita a los integrantes de la sociedad su inmersión en un universo de relaciones humanas con las cuales desarrolla su versión parcial de los fenómenos naturales y los somete a su idealización bajo una pretensión de universalización que lleva a la socialización de acuerdos que la erigen como “ciencia exacta” en la cual toda la comunidad humana queda sometida a la apropiación de sus paradigmas, como lo platea Kuhn en la estructura de las revoluciones científicas.

Vistas así, las operaciones matemáticas necesitan la didáctica que relacione los objetos del mundo real a los objetos del ideal humano, que describe o hace abstractos dichos objetos reales desde el principio de regularidad, de allí que la didáctica acuda al pensamiento espacial sensible que permita al nuevo integrante del grupo social ingresar al mundo cultural de la humanidad desde la acción de su relación con el entorno, porque la geometría “no solo se considera como una herramienta necesaria para describir el espacio circundante, comprenderlo e interactuar con él, sino que, como disciplina científica, descansa sobre importantes procesos de formalización que son ejemplo de rigor, abstracción y generalidad” (Castilblanco, A, Moreno L, p. 1), de allí que la didáctica puesta a disposición en el presente estudio doctoral, pretenda llevar, desde la socialización, a docentes del Departamento del Atlántico en la República de Colombia a la relación entre estos objetos matemáticos y los provenientes del desarrollo del pensamiento espacial desde los sistemas geométricos, para incitar a los integrantes de la comunidad educativa atlanticense a generar esquemas mentales en los nuevos integrantes de la comunidad académica, ligados o desarrollados desde las relaciones, que le permitan establecer marcos referenciales donde cobre sentido la lectura del entorno desde las operaciones matemáticas.

En el ejercicio de la socialización se han desarrollados múltiples jornadas pedagógicas en diferentes instituciones educativas y municipios del Departamento, en la cual se hace masivo el proceso didáctico iniciado, puesto en práctica y reflexionado en las relaciones entre la teoría y la práctica del docente investigador y desarrollado paulatinamente desde el año 1991, que alcanza su madurez en el ejercicio del docente en la Escuela Normal Superior Nuestra Señora de Fátima en el municipio de Sabanagrande y llega al departamento con los maestros egresados de dicha escuela y en el desarrollo u oportunidad que ha brindado el Programa “Todos a aprender, “PTA” del Ministerio de Educación Nacional de la Republica de Colombia al convocar al docente como tutor.

En las jornadas pedagógicas se han presentado las operaciones matemáticas como acciones que generan física o mentalmente en el ser humano, en la manipulación de los objetos sensibles bajo el dominio de su percepción del fenómeno natural en el uso de un marco referencial construido por el individuo y socializado a través de la lengua materna, una determinada regularidad, de allí la importancia de asumir la lengua materna como objeto matemático que facilita la comunicación de regularidades y su importancia en el desarrollo del pensamiento matemático. “Desde muy temprano en la vida del niño el tratamiento discursivo es aplicable a los objetos matemáticos” (Not, L, p. 308) y desde allí comienza la relación subjetiva-objetiva en la identificación de regularidades que le permiten reconocer las formas y características de los objetos reales circundantes y producir su percepción simbólica fónica de la lengua.

Estas acciones se presentan en tres categorías, las que construyen (arman), las que deconstruyen (desarman) y las que permiten observar las propiedades o raíces de los objetos finalmente construidos o deconstruidos (características del objeto que permiten su clasificación) y se establece la relación entre ellas y la construcción mental proveniente del pensamiento espacial desde el sistema geométrico, con lo cual el proceso didáctico materializa, hace sensible y perceptible las operaciones matemáticas, así se presentan las operaciones: adición, multiplicación y potenciación como constructoras de objetos matemáticos que permiten la lectura del medio y favorecen su aplicación y desarrollo de la memoria comprensiva desde la construcción de una determinada regularidad, mientras que las deconstructoras son: sustracción, división y radicación. Pues ellas desarman o deconstruyen objetos matemáticos establecidos como productos en espacios reales o imaginarios. En esta intervención se hace referencia a la doble naturaleza de la operación división como deconstructora y como constructora de objetos matemáticos a través de relaciones que generan la sensación de cambio, o productos que motivan apreciación de otros factores indispensables en la relación de esta ciencia con las otras áreas del conocimiento humano.La otra acción que produce operación matemática proviene de la observación, que da cuenta del número de raíces o propiedades dimensionales de los objetos geométricamente perfectos y ella es la logaritmación.

En las diferentes socializaciones se ha evidenciado la necesidad de establecer un proceso didáctico que desarrolle la memoria comprensiva antes que la memoria mecánica, “dado que el mundo en el cual se mueven los organismos con movimiento propio cambia continuamente, tanto el rango delpatrón de acción fijo como sus circuitos de interacción deben ser modificables” (Llinas, R, 2001, p. 201), a tal punto, que le permita al estudiante y a su maestro ejercitarse en la lectura del contexto,en la identificación de regularidades que le hagan posible establecer variantes e invariantes, se espera que estas socializaciones de algún modo modifiquen las prácticas pedagógicas y permitan la transformación del currículo de tal forma que los participantes puedan problematizar el contexto y generar argumentos que permitan el desarrollo de la misma matemática como ciencia en la cual el sujeto es quien relaciona el entorno con sus esquemas mentales para establecer regularidades, que le permiten limitar un fenómeno real de naturaleza compleja, en uno sintético limitado de lectura parcial, por lo tanto relativo y significativo para sus necesidades culturales.

La socialización se realizó como un medio para visibilizar la importancia del ambiente escolar para potenciar el pensamiento matemático de los educadores en ejercicio y desarrollar relaciones en las cuales la lengua materna juega un papel fundamental como objeto matemático que permite la adaptación a espacios variados dentro de características distintas, como considera Llinas, “si el <<cableado>> funcional de los patrones de acción fijo fuera tan rígido como el reflejo de rascarse …, simplemente no se hubieran dado maravillas como el lenguaje, tan dúctil para adaptarse a la complejidad de la comunicación humana y del pensamiento” (Llinas, R, 2001, p. 201) y de esta manera generar las relaciones que construyen regularidades y generan acuerdos en los grupos sociales, de allí la importancia de tenerlo en cuenta en la etapa de socialización del proyecto.

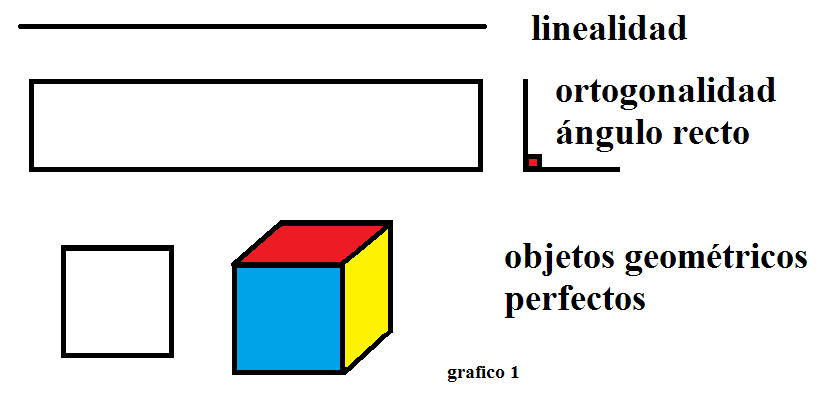
Esta se hace sobre la didáctica, que pretende desarrollar el pensamiento matemático de la comunidad educativa en instituciones escolares del Departamento del Atlántico, ella parte de los principios geométricos de linealidad (sucesión de elementos ordenados desde un marco referencial que permite establecer una relación biunívoca entre objetos del mundo real y símbolos del universo cultural, bajo la acción del conteo), ortogonalidad (relación establecida desde la linealidad que se genera en los arreglos rectangulares de objetos reales desde una regularidad numérica, hasta la construcción hipotética o teórica de ángulos rectos) y las propiedades dimensionales de los objetos geométricamente perfectos (el número de raíces que caracterizan un determinado objeto geométrico perfecto). Ver gráfico 1

Desde esta visión generada en el proyecto de investigación realizado en los antecedentes del presente se pretende evaluar el impacto en el ambiente escolar, de una didáctica que estimula la lectura creativa de la realidad desde las operaciones matemáticas. Para esto se ha realizado un diálogo dentro de un discurso pedagógico que ha pretendido mostrar estas acciones a los maestros y generar la construcción de marcos referenciales desde la acción discursiva que implican procesos didácticos que construyen y generan regularidades, que el maestro y sus discípulos pueden vivenciar e interpretar haciendo emerger el objeto geométrico y el pensamiento de comparación que establece una métrica que genera el quantum; este proceso, aun cuando se hace desde lo colectivo, hace los esquemas mentales del individuo, por ellos es indispensable tener en cuenta las etapas evolutivas del sistema nervioso central de los participantes en el proceso educativo así como la etapa sicológica del mismo, ocupación de este proceso investigativo, que lleve a superar las estructuras de poder establecidas en la educación matemática desde un domino abstracto de la teoría a uno que se genera en las lecturas parciales desde las relaciones construidas en las interacciones dialógicas que permiten la idealización individual y colectiva.

Como señala Paulo Freire en la educación como práctica de la libertad, no hay diálogo con la estructura de gran dominio, porque el diálogo implica una mentalidad que no florece en áreas cerradas autárticas. Estas, por el contrario, constituyen un clima ideal para el antidiálogo. Para la verticalidad de las imposiciones. Para robustecer a los señores. Para el mandonismo. Para la ley dura hecha por el propio poseedor del conocimiento, no importa que las relaciones humanas entre dador del conocimiento y recibidor sean, en ciertos aspectos, suaves. Hay paternalismos con descendencia del “adulto” hacia el “menor” así que en tales circunstancias, aunque se hable de bondad de su “comprensión humana” de su “condescendencia”, condescendencia y bondad (p. 63) no brinda la posibilidad de contextualizar las estructuras matemáticas desde el imaginario de los interactuantes, por lo tanto esclaviza el pensamiento hasta el punto de negar sus propias capacidades genéticas y despreciar así sus habilidades del pensamiento, lo que plantea la necesidad de observar la interacción en el aula y el impacto en el desarrollo del pensamiento matemático en este proceso de investigación.

En la etapa de este proyecto en el proceso evaluativo se pretende sistematizar, desde una investigación de corte cualitativo, aspectos sobre la importancia del ambiente escolar para desarrollar el pensamiento matemático bajo la interpretación creativa de una realidad, donde el diálogo produce las regularidades y estable los espacios para observar características y propiedades; para este tipo de intervención en el aula se hace necesario generar un proceso de expectativas en el docente para que acceda a participar voluntariamente en él, y esta constituye la primera etapa del proyecto, la socialización. Para ello se realizó una serie de encuentros con docentes en jornadas pedagógicas, sobre la didáctica y la necesidad de contextualizar la teoría matemática para hacerla asequible a la curiosidad del niño y del joven, teniendo como base la ideas de que:

(…) resulta fácil comprender cómo las necesidades, sobre todo orgánicas del principio, pueden subordinarse poco a poco a unas necesidades funcionales, y cómo éstas pueden originar unas operaciones que afectan a las relaciones de las cosas entre sí y ya no solamente a las relaciones de las cosas con los órganos del propio cuerpo. (Piaget, J, 2011, p. 230)

De ahí que en la socialización del proyecto se desarrollen talleres en los cuales se pretende contextualizar los estudios realizados por el estudiante del Doctorado en una construcción de regularidades donde las acciones que se materializan con los objetos del entorno y cumplen con las afirmaciones de la teoría, desde los sistemas numéricos y desde el plano geométrico, produzcan algún tipo de interés en los docentes y observar el avance de la propuesta en el colectivo, en este medio se asumirá como objeto de estudio del impacto la invitación del docente investigador a otra serie de talleres y de acompañamiento en el aula de clase con los maestros en ejercicio, para los maestros en formación se abriría una serie de seminarios para la reflexión de la práctica pedagógica desde esa perspectiva. Si la participación no logra la motivación y no se producen otras invitaciones a dicha comunidad, se asumirá que el impacto no causó muchas expectativas y se procederá a recoger información en los que inicialmente realizaron para observar el impacto del primer taller; para la recolección de datos y analizar el impacto en sitio, se observará el desarrollo de la práctica pedagógica en la I.E. Técnica Agropecuaria de Puerto Giraldo y sus tres sedes, María Inmaculada, Rafael Núñez y Las Flores.

Este desarrollo permitirá observar a los participantes voluntarios, para escuchar sus inquietudes y su visión particular de los fenómenos matemáticos y el desarrollo teórico de los mismos planteados desde esta perspectiva y desde allí generar la acción dialógica que fomenta el aprendizaje mutuo desde fenómenos salientes, por cuanto, al decir de Martínez, “ahora bien , el estudio de entidades emergentes requiere de una lógica no deductiva; requiere una lógica dialéctica en la cual las partes son comprendidas desde el punto de vista del todo” (Martínez, M, p. 101), allí los que interactúan producen acciones colaborativas y cooperativas, que potencian la observación que dará identidad a quienes asuman el desarrollo del mismo proyecto, de quienes decidan no participar activamente en él, será únicamente de observación sobre el impacto del taller inicial, para inferir posibles actuaciones didácticas y pedagógicas motivadas, o analizar la fuerza de la tradición didáctica y pedagógica del maestro en sus clases ordinarias y desde el proceso de participación de los docentes en ejercicio o en formación en la aplicación de los conceptos didácticos de las operaciones matemáticas desde los conceptos de construcción, deconstrucción y de propiedades dimensionales de los objetos geométricamente perfectos.

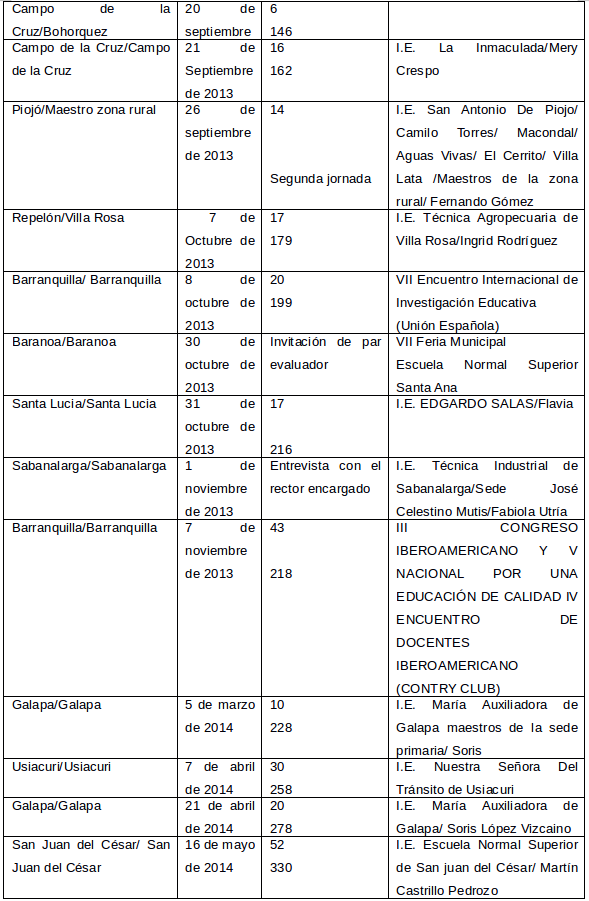
En la búsqueda de la forma de incidir en el ámbito de la escuela y en el aula de clase, que es efectivamente en donde se lleva a cabo la interacción social que se realiza como acto educativo, y se generan las diferentes interacciones que permiten el ingreso paulatino a la cultura académica humana. “(…) la constitución de aptitudes innatas y la regresión de los programas genéticos o <<instintos>> es indisociable de la preexistencia de un marco cultural qué actúe, a un mismo tiempo, como sistema organizador y como medio ambiente” (Morin, E, 2005, p. 101). Y para incidir directamente en el ruido cerebral que producen las ideas en el dialogo con los docentes, se ha desarrollado la serie de talleres en las siguientes poblaciones con maestros en ejercicio:

Para poder generar un proceso que construya el ambiente escolar en que transcurren las interacciones del día a día en las instituciones educativas se hace necesario generar en el maestro en ejercicio el deseo por leer y transformar su realidad desde los procesos de lectura y escritura creativa del medio y desarrollar las diferentes tipologías de estas, que le permitan tener en cuenta sus propias habilidades básicas del pensamiento (observar, comparar, clasificar, describir, relacionar) fundamentales para alcanzar los objetivos de una educación que permita al maestro y al estudiante interactuar bajo el interés de la mutua alimentación académica, tal como lo señalan múltiples investigaciones como los estudios -Llece-Unesco (2008), entre otras- las cuales han evidenciado que el clima escolar tiene una incidencia de entre el 20% al 50% cuando se explican los resultados de los estudiantes.

El desarrollo empírico que puede observarse en las acciones del aula que construyen percepción y desde allí opinión, que con la motivación didáctica y pedagógica lleva a la argumentación, genera espacios democráticos en las instituciones educativas, que desatan el desarrollo de actitudes y aptitudes que le llevarían al ejercicio de habilidades y destrezas para analizar, argumentar e interpretar su realidad, lo que generaría la aplicación del legado cultural de la humanidad (teoría) en la acción práctica, con lo cual se genera la potencialización del estudiante que le ayuda a reconocerse a sí mismo en sus limitantes y posibilidades de desarrollo con lo cual evita los bajos desempeños, porque la principal acción del aula de clases en el desarrollo del pensamiento matemático, es llevar de la mano al niño o adolescente para ingresarlo al mundo de la cultura humana de la matemática y hacerlo consciente de sus capacidades genéticas para la aplicación de dicha teoría, “(…) los investigadores activos admiten que las transformaciones de la realidad social no se consiguen sin interesar el entendimiento de los agentes” (Carr, W.,Kemmis, S., Martínez Roca,1988, p. 192) con lo cual se evita el deterioro del clima escolar que es un común denominador en la educación matemática del planeta.

El clima escolar genera el ambiente necesario para la construcción de un espacio democrático de calidad, porque tiene múltiples impactos, al ser un sistema en donde todos los agentes involucrados en el acto educativo construyen sus relaciones, donde tanto los educandos como los educadores incrementan la motivación por aprender; este principio es asertivo si crece la autoconfianza, se fomenta la observación y la opinión como una puerta de ingreso a la argumentación, con lo cual se obtiene una mejor actitud del estudiante en el aula y en el entorno escolar, se mejoran las relaciones y los procesos educativos y con ello los desempeños escolares, se potencia el aprendizaje efectivo de valores y de cultura democrática, se disminuyen los conflictos entre pares al favorecer el desarrollo de la lógica, con la cual el individuo interactúa, lo que lleva al análisis de todas y cada una de las acciones con las cuales generamos pensamiento matemático, claro está, teniendo en cuenta las etapas evolutivas y de desarrollo del sistema nervioso central pues,

(…) un niño puede haber captado el concepto de que para sumar dos números le basta contar, a partir del primero tantos “puntos” como exprese el segundo y, sin embargo, puede que no sepa comprender, ni de lejos, la estructura complicada de la operación … en la que ha de hacer agrupamientos y reagrupamiento … hablando en otros términos, los conceptos matemáticos y los procesos deben adquirirse, ante todo, en su forma pura…”. (Dienes, Z.P., p. 38)

De esta forma se puede bajar sustancialmente la deserción escolar.

El docente en su proceso de ingresar al niño y al adolescente a la cultura humana de la matemática, puede observar que, desde la lectura creativa de su entorno, puede desatar sus habilidades básicas del pensamiento, que les facilita mirar el fenómeno de lo complejo a lo simple y de lo simple a lo complejo, y puede pasar de seguidor de una determinada teoría a asumirse como diseñadores o modeladores de ambientes de aprendizaje, en los cuales las bases teóricas de la matemática son el sustento del accionar en el aula de clases, así ellos construyen el marco referencial para generar una determinada regularidad, e incrementar sus propias potencialidades en la conciencia misma de su saber matemático, con lo cual se construye sentido de vida, utilidad práctica y consolidación de saberes de una memoria que se acostumbra al estudio para la comprensión de un determinado fenómeno natural (memoria comprensiva).

Los pedagogos han clarificado, entre otras cosas... que la experiencia formadora requiere de confirmación por parte del alumno. La experiencia formativa es la que puede confirmarse, es la experiencia abierta, que implica varias posibilidades, que responde preguntas o cuestionamientos vitales, que sugiere alternativas o caminos de solución que el estudiante puede pensar, elegir y evaluar.(Flórez Ochoa, R.,1999, p. 97)

En el mismo desarrollo de su actividad como docentes, este adquiere la dinámica de acompañante en la potencialización de la habilidades del pensamiento de sus discípulos, por lo tanto el ejercicio de un tipo de liderazgo y respeto generado en la acción dialógica de la promulgación de las ideas culturales matemáticas, con lo cual se desarrolla un tipo de pertenencia a la institución escolar que permite recuperar, incrementar y consolidar la autoridad académica horizontal del docente ante los educandos, con ello se construye una mejor motivación laboral, que disminuye síndromes de estrés laboral, y genera la base de un aprendizaje cooperativo o colaborativo donde el mismo docente no escapa a la modificación permanente de sus esquemas mentales por la acción del grupo desde la misma dinámica de la cultura democrática, con lo cual obtiene mayores niveles de desarrollo profesional, didáctico y pedagógico, una mejor comprensión del fenómeno cultural matemático y un acercamiento a la potencialización de todos y cada uno de sus estudiantes desde sus competencias.

(…) las competencias brindan una muy potente posibilidad para repensar los fines de la educación y una muy adecuada oportunidad para volver a pensar el currículo, de manera que podamos orientar el trabajo priorizando el desarrollo integral de los estudiantes y no el aprendizaje, como hasta el momento ha sido dominante a nivel escolar. (Zubiria, J., 2013, p. 158)

En la institución educativa también se generan múltiples impactos, especialmente en la ampliación de su capacidad formativa y de su influencia en la transformación de la cultura, en la disminución de conflictos internos, en generar una mayor equidad en la distribución de la actitud de análisis, lo que genera aprendizajes de los estudiantes, en el incremento de su reputación y en que la institución sea asumida como un modelo de referencia para la organización social dentro del entorno comunitario local, desde el establecimiento de marcos referenciales dentro de una cultura democrática que incentiva el reconocimiento de diversas lógicas con las cuales se construye una realidad y se argumenta, desde regularidades que generan el desarrollo del pensamiento matemático.

LA NECESIDAD DE FORMAR A LOS DOCENTES EN DIDÁCTICA Y PEDAGOGÍA PARA DESARROLLAR EL PENSAMIENTO MATEMÁTICO EN AMBIENTES ESCOLARES PARTICIPATIVOS

LA ETAPA DE SOCIALIZACIÓN EN SITIO

(METODOLOGÍA)

Comienza la socialización en el municipio de Ponedera, corregimiento de Puerto Giraldo (6 de marzo de 2013) docentes participantes 30. I.E. Técnica Agropecuaria de Puerto Giraldo/ Sede María Inmaculada, Rafael Núñez y Las Flores.

El día 6 de marzo de 2013, en diálogo con la rectora, ante la cual se presenta el investigador Juan David Romero Serna, como tutor del programa “Todos a aprender “ y la líder académica Institucional, Especialista Doris María Ojeda Casalins, se generó información sobre la formación académica del tutor investigador y su intencionalidad de presentar a la comunidad educativa la propuesta didáctica y pedagógica que este ha desarrollado a lo largo de 23 años de su vida para generar el estudio de impacto de la didáctica y la pedagogía en dicha institución.

Al presentar la propuesta a la rectora se notó una total concentración en la muestra que hacía el investigador, se escucharon expresiones de parte de ella como “así la matemática es muy comprensible”, “a mí no me enseñaron así”, “de haber visto la matemática así hoy sería licenciada en matemáticas”, todas ante las personas que allí estaban presentes. Se acordó presentar la propuesta a los maestros y esperar su respuesta. Así se inicia la etapa de socialización en la I. E. Técnica Agropecuaria de Puerto Giraldo.

La socialización en esta sede María Inmaculada de la I.E. Técnica Agropecuaria de Puerto Giraldo, se inicia como parte de un compromiso laboral del tutor investigador en el programa “Todos a aprender”.

Allí se plantea a los maestros la propuesta didáctica y pedagógica para ser llevada al aula de clases. La impresión que se generó en el maestro investigador fue que en sus interlocutores de esta sede no hubo un total convencimiento, pero aceptaron colaborar en el proyecto, para lo cual se programó una jornada pedagógica donde se mostrara el proceso didáctico y pedagógico para el desarrollo del pensamiento matemático bajo la lectura creativa del entorno.

LA SOCIALIZACIÓN EN LA SEDE LAS FLORES

La presentación de la propuesta en la sede Las Flores parecía haber generado un interés en algunos maestros, por lo menos no se presentaron objeciones a la propuesta y se generó un diálogo muy fluido donde se acordó hacer la jornada pedagógica para presentar la propuesta y generar acuerdos de aplicación o no a nivel institucional, allí se observó que los docentes se interesaron por ver cómo sería la didáctica y la pedagogía aplicada en el aula.

LA SOCIALIZACIÓN EN LA SEDE RAFAEL NUÑEZ

El proceso de socialización en la sede Rafael Núñez se realizó en diálogos con los docentes y la coordinadora, la Esp. Cándida Isabel Salazar Ariza, quien se notó algo receptividad a la propuesta didáctica y pedagógica para el desarrollo del pensamiento matemático desde la lectura creativa del medio.

JORNADA DIDÁCTICA Y PEDAGÓGICA PARA LA PRESENTACIÓN DE LA PROPUESTA

Esta jornada se realizó con todos los docentes en la sede María Inmaculada, se presentó el desarrollo didáctico y pedagógico para hacer la lectura creativa de la realidad desde la interpretación argumentada, desde el saber específico de las matemáticas en el uso del pensamiento espacial y los sistemas geométricos, para aplicar las operaciones matemáticas teniendo en cuenta el proceso evolutivo del pensamiento humano. Allí se evidenció la preocupación del maestro por los algoritmos para realizar las operaciones matemáticas, que al parecer del investigador cede espacio a la identificación del fenómeno matemático para la conceptualización de la teoría bajo argumentos establecidos en el devenir histórico de esta.

El material didáctico presentado llamó la atención de la gran mayoría de los maestros asistentes a la jornada pedagógica. La falta de medios para presentar las diapositivas solo concentró a los maestros en las actividades con dicho material y la interpretación que se hacía mediante el establecimiento de regularidades por parte del maestro investigador que animó la jornada. La forma como se exploraron los conceptos, como se inducía el pensamiento de los participantes mantuvo la atención del auditorio, solo una maestra entró en etapa de somnolencia, una entraba y salía dando más una importancia a otra actividad y otro profesor abandonó la jornada antes de que terminara, sin ningún argumento hasta el día de hoy.

LA ESTRATEGIA DIDÁCTICA Y PEDAGÓGICA LLEVADA AL AULA DE CLASES EN LA I.E. TÉCNICA AGROPECUARIA DE PUERTO GIRALDO

Aplicar una estrategia didáctica y pedagógica que incite a generar grandes interrogantes sobre lo que se ve, se siente y se interactúa, implica reconocer una nueva epistemología en el medio, “esto implica el reconocimiento crítico de esta situación, a fin de lograr, a través de una acción transformadora que incida sobre la realidad, la instauración de una situación diferente, que posibilite la búsqueda del ser…” (Freire P, 2005, p. 45), desde su propio saber sobre el saber constructivo de la matemática, y hacer un acercamiento a este desde la filosofía kantiana de saber eminentemente empírico, lo que generaría una serie de actuaciones con las cuales se desarrollan habilidades del pensamiento y llevaría a los docentes a construir en el aula ambientes de aprendizaje acogedores, inclusivos y respetuosos de las visiones de sus estudiantes y aparecería la necesidad de argumentar los fenómenos observados desde el devenir histórico cultural de la matemática apoyados en el uso de la lengua materna y en la interacción didáctica pedagógica que genera lenguaje especifico del saber matemático.

 ¿Qué impide a los directivos docentes y a los docentes generar en la institución educativa un clima y una cultura escolar participativa, inclusiva, democrática y de argumentación propia del saber específico de la matemática? Es evidente que el docente no solo enseña lo que sabe, sino que aprehende en la interacción tanto saber matemático como didáctico y pedagógico. A su vez los estudiantes aprehenden de sus profesores y generan aplicabilidad de lo que aprehenden, si se parte de hacer marcos referenciales del entorno para describir los fenómenos desde las regularidades que emergen de dicha interacción y, primordialmente, desde sus propios esquemas mentales, lo cual se manifiesta en el tipo de interacciones que, con sus actitudes y actuaciones, construyen el ambiente educativo.

El cómo se enseña termina siendo el qué se enseña. Y el cómo se enseña está relacionado con lo que los docentes aprendieron en sus historias pedagógicas y didácticas, las cuales usualmente estuvieron signadas por métodos centrados en la conservación de la teoría en la memoria repetitiva y su proceso motivador era el miedo, el autoritarismo y la exigencia de disciplina bajo una relación de mando y obediencia, de allí la necesidad de generar otra cultura desde otra epistemología para el desarrollo del pensamiento matemático, que implique “la necesidad de idear una explicación … fuerte si se pide a los alumnos producir fenómenos que son imposibles de visualizar” (Castilblanco, O, 2004, p. 46).

Es así como se ha observado que los maestros plantean situaciones distintas a sus estudiantes desde la didáctica de construcción y deconstrucción de regularidades visibles desde los argumentos instituidos por la teoría matemática, así el estudiante, desde los primeros años de escolaridad observa secuencias que construyen en la realidad o en la imaginación segmentos de recta y los asocia con adiciones. Lo que permite observar lo planteado por Jean Piaget (p.397), en el nacimiento de la inteligencia en el niño, en lo cual la acomodación de las características de los nuevos medios puede prolongarse, mediante el estudio de conductas más complejas, siendo este tipo de experiencia de naturaleza tal que permite proseguir el examen de relaciones entre esquemas dinámicos y la percepción o representación visual.

Y de allí puede propiciar las adiciones de cantidades iguales como multiplicaciones, lo que nos lleva a los arreglos rectangulares de objetos, así se hace evidente la diferencia entre operaciones matemáticas y se establecen relaciones que posibilitan la construcción de esquemas mentales que hagan posible la aplicación contextual del saber matemático. Se produce la generación de situaciones de las cuales emergen problemas y con ello aparece la necesidad de codificar y decodificar desde los procesos de observación del entorno que incitan a la escritura, este tipo de educación no se preocupa por almacenar información en el sistema nervioso central sino que se ocupa de desarrollar las habilidades básicas del pensamiento, desde la comprensión de los fenómenos naturales del entorno y la solución de necesidades del sujeto que interactúa con su medio y así construye, soluciona y aplica en contexto la teoría en sus problemas. Juan Miguel González en teoría educativa transcompleja citando a Minnick, y Alvermann señala que:

Los seres humanos estamos inmersos a lo largo de nuestras vidas en aprendizajes y enseñanzas. En este sentido, bajo la visión compleja de la realidad, un problema se hace solución y la solución otro problema, así como lo aprendido también deviene. A este singular proceso, llamaremos desaprendizaje y reaprendizaje, porque nada está dicho como verdad. (p. 79)

En la medida que el maestro utiliza y afina sus propios recursos e interpreta la operaciones matemáticas como acciones de construcción y deconstrucción, genera discursos pedagógicos centrados en regularidades, construidos bajo un marco referencial y en uso de una epistemología que vence poco a poco la resistencia a las lecturas creativas, a la generación de problemas y argumentos matemáticos entrelazados con el medio y se hace común que los docentes tengan claro qué tipo de ambiente de aprendizaje deben construir en el aula y en la escuela, pero que interiormente avanza progresivamente, pues desde su cosmovisión, el medio como recurso didáctico vence y genera nuevos paradigmas, que establecen marcos referenciales que permiten la regularidad desde donde puede observar el mundo, y es allí donde se construye sentido y se otorgan significados e interactúan, la práctica cotidiana los lleva a generar ambientes educativos democráticos participativos como medio para favorecer sus propósitos.

En las operaciones deconstructoras se hace evidente cuando se acciona para desarmar líneas productos u objetos (sustracción, división [con una doble naturaleza desarma el ángulo recto y genera producto como razón de cambio] y radicación); bajo esta didáctica, interpretar la realidad desde la sustracción equivale a identificar el desarmar líneas o grupos de objetos desde una acción práctica, de esta forma se puede utilizar la didáctica que genera experiencia y se desarrollan habilidades del pensamiento desde la descripción del fenómeno natural que utiliza un marco referencial visible y otro en el cual ubica los elementos que sustrae en la acción de realizar la operación, de esta forma se pueden llevar las acciones a grados iniciales de escolaridad.

Ello se comprende porque en los procesos de formación inicial, en la medida en que el niño identifica acciones desde la manipulación de los objetos concretos, aprende; la didáctica y la pedagogía aplicada por el maestro puede ser abordar estas temáticas de las operaciones matemáticas desde los espacios lúdicos de construcción y deconstrucción, lo que genera experiencia matemática en el niño desde las relaciones que él construye en la búsqueda de generar regularidades para interpretar una determinada realidad, así el maestro logra que se haga evidente para el niño que la matemática es un saber constructivo en el cual hay que asumirse como generador de marcos referenciales, lo que hace emerger ambientes educativos democráticos de experimentación e interpretación de una realidad con la cual el sujeto construye la regularidad operando y accionando con su entorno.

Pero las operaciones no son solo acciones interiorizadas: para que haya operaciones, es necesario además que estas operaciones se hagan reversibles y se coordinen formando estructuras de conjunto, estructuras que pueden entonces expresarse con términos del algebra general: “agrupamientos”, “grupos”, “latices” (retículos), etc.(Piaget J, 1999, p.118)

  En la reversibilidad para el tratamiento de la división se observa el fenómeno matemático que permite tomar un producto y dividirlo (fraccionarlo, quebrarlo, racionalizarlo) para generar partes de un todo, de allí que para asumirlo inicialmente como un deconstructor (desarmador) del ángulo recto, se hace evidente que el fenómeno consiste en tomar un producto y establecer una relación de acción en el cual se establecen grupos de una misma cantidad, ante esta situación los maestros han expresado su preocupación por el algoritmo de esta operación, durante cuya práctica pedagógica del aula, se han desarrollado procesos en los cuales se demuestra la importancia de establecer los primeros nueve términos de la sucesión calculada a partir de asumir el primer término de ella teniendo en cuenta el valor del divisor.

Al analizar la otra naturaleza de la operación división como razón de cambio (en todo fenómeno natural que al ser percibido por los sentidos lo hace como un cambio, la operación implicada es la división) se fomenta la actuación didáctica y pedagógica de acciones de un antes y un después, la experiencia para hacer notar al estudiante que las operaciones matemáticas las podemos utilizar desde los espacios sensoriales, de esta forma se puede generar experiencia didáctica para señalar la división que se ve, que se siente, que se escucha, lo que abre la matemática al uso indiscriminado de la imaginación, pues este está ligado en muchos casos a la noción del tiempo. Tratado ampliamente por Jean Piaget en “El desarrollo de la noción de tiempo en el niño”, este fenómeno genera la necesidad de reconocerla en el uso de las relaciones culturales, como cambio de papel moneda internacional, porcentajes, etcétera y la aplicación de razones y proporciones.

Esto explica el hecho de que todas las personas, sin importar el grado de escolaridad, operan en la cotidianidad en acciones de construcción y deconstrucción de fenómenos matemáticos, ya sea como observadores del entorno o de sí mismos, y lo que se debe pretender en la escuela es hacer conciencia del tipo de observador que es la persona, con la cual se establecen relaciones entre el imaginario individual y el colectivo, sobre la base de una operación consciente que nos lleva a establecer juicios y conclusiones desde una lógica que es posible argumentar desde una tradición crítica que utiliza el devenir histórico del conocimiento matemático, incluso desde muy corta edad aprovechando el saber predictivo, aprovechando la igualación de las duraciones sincrónicas y la transitividad de las relaciones de igualdad en el tiempo, explicitas por Jean Piaget en la segunda parte “El tiempo físico…” en el capítulo cinco el desarrollo de la noción de tiempo en el niño.

Generar procesos que desarrollen habilidades del pensamiento es disponer emocionalmente al sujeto a confiar en su racionalidad respecto a aquello que observamos, sin detenerse a pensar en la incapacidad para resolver problemas, sino en prever y comprobar validez de los datos generados en las interpretaciones que este realiza. Para lo cual se asume el error como una posibilidad de una interpretación que no satisface el interés del observador, lo que genera un proceso de autoevaluación individual y de evaluación cuando se genera la cultura democrática de la escucha y del juicio racional del grupo.

Esto permite afirmar que se evalúan automáticamente los hechos a través de las lentes que al observador le sirven para interpretar el medio (las creencias básicas, los valores, los metarrelatos, las teorías y paradigmas) que se incorporan a lo largo de la historia personal, y desde esa valoración se generan argumentos que avalan o corrigen conductas que responden a una lógica implícita en el desarrollo de una cultura, de allí el acercamiento a una nueva epistemología de la matemática para el medio.

Anexo

Cibergrafía

Pagina web Newton.cneci. Disponible en:

http://newton.cnice.mec.es/materiales_didacticos/energia/conservacion.htm

Cerezo, H. Corrientes pedagógicas contemporáneas. Disponible en: www.odiseo.com.mx/2006/07/cerezo-corrientes.html

Morin, E. El método I. Multidiversidad mundo real. Disponible en:

www.transformacioneseducativas.org,

wwcienciasdelacomplejidad.org,

www.encuentrosedgarmorin.org,p23

http://www.tdx.cat/bitstream/handle/10803/2507/03.Justificacion_de_la_tesis.pdf?sequence=5

http://www.mineducacion.gov.co/1621/w3-article-310659.html