Metodología para la priorización de la entrega de ayudas humanitarias en el contexto de la pandemia covid-19,
utilizando la herramienta QFD Fuzzy

Methodology for prioritizing the delivery of humanitarian aid in the context of a COVID-19 pandemic using the QFD Fuzzy tool

Metodologia para priorizar a entrega de ajuda humanitária no contexto da pandemia covid-19, usando a ferramenta QFD Fuzzy

Andrés Mauricio Paredes Rodríguez a* | Juan José Rojas Reyes b | Diego León Peña Orozco c

a https://orcid.org/0000-0001-9196-9965 Corporación Universitaria Minuto de Dios, Buga, Colombia

b https://orcid.org/0000-0001-5252-3020 Corporación Universitaria Minuto de Dios, Roldanillo, Colombia

c https://orcid.org/0000-0002-4301-0271 Corporación Universitaria Minuto de Dios, Buga, Colombia

• Fecha de recepción: 2020-12-12
• Fecha concepto de evaluación: 2021-03-21
• Fecha de aprobación: 2021-03-23

  https://doi.org/10.22335/rlct.v13i2.1371

  Para citar este artículo / To reference this article / Para citar este artigo: Paredes, A. M., Rojas, J. J. & Peña, D. L. (2021). Metodología para la priorización de la entrega de ayudas humanitarias en el contexto de la pandemia covid-19, utilizando la herramienta QFD Fuzzy. Revista Logos Ciencia & Tecnología, 13(2), 72-84. https://doi.org/10.22335/rlct.v13i2.1371

  * Autor para correspondencia. Correo electrónico: aparedesrod@uniminuto.edu.co

  Resumen

  El impacto de la disrupción causada por el covid-19 ha generado en los gobiernos locales múltiples retos relacionados con la toma de decisiones, tales como la priorización de familias afectadas de acuerdo con su nivel de vulnerabilidad, para garantizar una asignación equitativa de ayudas humanitarias. Este artículo propone un marco metodológico basado en el método de despliegue de función de calidad difuso (QFD Fuzzy) para priorizar familias afectadas por el covid-19, considerando variables como cobertura de poblaciones afectadas, tiempos de privación, eficiencia en costos y seguridad en la entrega. La metodología propuesta es probada utilizando datos sintéticos obtenidos de una muestra de 1000 familias, con el propósito de establecer el orden de atención de la población en una ciudad del centro del Valle del Cauca. Este documento establece una estrategia que ofrece a un gobierno mayor efectividad en la toma de decisiones para atender una emergencia sanitaria como la del covid-19, que apoya la intención humanitaria envuelta en esta gestión. Es necesario insistir, en todo caso, que no se trata de una metodología que pueda ser estática, por lo que se deben considerar de manera pertinente las variables que puedan surgir como indicadores de vulnerabilidad. Esto se presenta como una investigación futura complementaria.

  Palabras clave: ayuda humanitaria, covid-19, aapriorización, QFD Fuzzy, toma de decisiones

  Abstract

  The impact of the disruption caused by Covid-19 has generated in local governments, multiple challenges related to decision-making, such as prioritizing affected families according to their level of vulnerability to guarantee an equitable allocation of humanitarian aid. This article proposes a methodological framework based on the fuzzy quality function deployment method (QFD Fuzzy) to prioritize families affected by Covid-19 considering variables such as coverage of affected populations, deprivation times, cost efficiency and delivery security. The proposed methodology is tested using synthetic data obtained from a sample of 1000 families in order to establish the order of care of the population in a city in the Center of Valle del Cauca. This document establishes a strategy that offers a government greater effectiveness in making decisions to attend a health emergency such as COVID-19, which supports the humanitarian intention involved in this management. In any case, it is necessary to insist that it is not a methodology that can be static, for which it is necessary to force it to read in a pertinent way the new variables that may arise as indicators of vulnerability. This is presented as supplementary future research

  Keywords: Humanitarian Aid, COVID-19, Priorization, Decision Making, QFD Fuzzy

  Resumo

  O impacto da interrupção causada pela Covid-19 gerou vários desafios relacionados à tomada de decisões nos governos locais, como priorizar as famílias afetadas de acordo com seu nível de vulnerabilidade, para garantir uma alocação equitativa da ajuda humanitária. Esse artículo propõe um marco metodológico baseado no método de desdobramento de função de qualidade difusa (QFD Fuzzy) para priorizar famílias afetadas pela Covid-19, considerando variáveis como cobertura de populações afetadas, tempos de privação, eficiência em custos e segurança na entrega. A metodologia proposta é testada a partir de dados sintéticos obtidos de uma amostra de 1000 famílias, a fim de estabelecer a ordem de atendimento à população de um município do centro do Vale do Cauca. Este documento estabelece uma estratégia que oferece a um governo maior eficácia na tomada de decisões para atender uma emergência de saúde como a Covid-19, que apoia a intenção humanitária envolvida nesta gestão. É necessário insistir, em qualquer caso, que não se trata de uma metodologia que possa ser estática, motivo pelo qual as variáveis que podem surgir como indicadores de vulnerabilidade devem ser consideradas de forma pertinente. Isso é apresentado como pesquisa complementar futura.

  Palavras-chave: ajuda humanitária, covid-19, priorização, QFD Fuzzy, tomada de decisão

  Los desastres causados por la naturaleza, por las enfermedades o por la acción humana plantean la necesidad de planear y ejecutar distintas actividades que tienen como objetivo la reducción de la pérdida de vidas y el alivio del sufrimiento de la población afectada, proceso que se conoce como logística humanitaria (Shao et al., 2019). Las cadenas de suministro humanitarias se encargan de la coordinación, gestión y planeación de actividades relacionadas con la respuesta a desastres a través de la administración de flujos de personas, información, equipos y materiales. Hoy en día, la gestión de cadenas de suministro humanitarias tiene un alto grado de complejidad, debido a factores como la imprevisibilidad de la demanda de los damnificados, el entorno con infraestructura desestabilizada (es decir, el acceso limitado a carreteras o fuentes de energía), las presiones de tiempo y la falta de recursos (Hashemi et al., 2020). Dentro de las operaciones de logística humanitaria se encuentra la distribución de ayudas humanitarias, la cual busca entregar alimento a las familias damnificadas, con el propósito de garantizar su seguridad alimentaria en tiempos de crisis y al menor costo posible (Balcik et al., 2008).

  La entrega de alimentos es considerada hoy en día no solo como una estrategia que garantiza la seguridad alimentaria de la población, sino que también es un medio para lograr la paz y la justicia en los territorios con población altamente vulnerable. Por ejemplo, Mary & Mishra (2020) analizan el efecto que tiene la entrega de alimentos con enfoque humanitario en el desarrollo de las guerras civiles, utilizando una muestra de 79 países receptores entre 2002 y 2017. El análisis explora la variación transversal y temporal en los desplazamientos humanitarios de ayuda alimentaria entre países. Las estimaciones de las variables instrumentales de referencia implican que un aumento del 10 % de la ayuda alimentaria humanitaria per cápita disminuye la incidencia del conflicto civil en aproximadamente 0.2 puntos porcentuales (o en un 0.9 % en la incidencia media del conflicto). La ayuda alimentaria humanita-
  ria también disminuye la incidencia de conflictos civiles a pequeña y gran escala, así como el inicio y la duración de estos.

  La disrupción del covid 19 ha obligado a que las ciudades se enfrenten al reto de administrar eficientemente sus recursos, con el objetivo de atender a la población más población más damnificada, considerando aspectos como la seguridad alimentaria. Entre las decisiones que deben tomar los gobernantes se encuentra la distribución de ayudas humanitarias, tales como los kits alimenticios. No obstante, existe una problemática asociada a estos fenómenos y es que la demanda de mercados por parte de las familias damnificadas comúnmente desborda la oferta del sistema. Por esta razón, se hace necesario diseñar una herramienta que permita a los administradores de las donaciones realizar una priorización de las familias a atender, buscando establecer un orden de priorización según el nivel de vulnerabilidad que presenta cada solicitante. Con el objetivo de determinar la metodología de la presente investigación, se realiza la revisión de literatura sobre entrega de víveres y ayudas humanitarias, mediante la cual se logran establecer algunos referentes, que se presentan a continuación con su principal aporte.

  En primer lugar se encuentra la investigación de Suzuki (2019), en la cual se analiza la efectividad de los dos enfoques de solución más comunes al problema de distribución de ayudas a los sobrevivientes de un desastre, lo que comúnmente se conoce como distribución en la última milla. La primera solución analizada es el método p, donde el material más urgente siempre fluye primero hacia las zonas de desastre. El segundo enfoque es el método m, en el cual los envíos que ingresan a la zona afectada están compuestos por materiales con un grado de urgencia alto, pero también por artículos de baja prioridad. Los autores desarrollan un modelo matemático y realizan distintos experimentos numéricos, con los cuales logran probar que en el 83.3 % de los casos analizados el método m es más efectivo, a pesar de que en la realidad es el menos utilizado.

  Por otra parte, Li et al. (2018) examinan la estructura general de las cadenas de suministro de ayuda humanitaria, con el propósito de desarrollar un modelo de máxima cobertura cooperativa que considere las restricciones de presupuesto y el aumento de los beneficios para la población afectada. Los autores analizan el impacto que tiene la disponibilidad de productos en los centros de ayuda humanitaria sobre el desempeño general de la cadena, a través de la simulación de casos de estudio teóricos. Siguiendo este enfoque, Naji-azimi et al. (2012) desarrollan un modelo de ubicación satelital de los centros de distribución, desde los cuales se pueda suministrar ayuda humanitaria a personas afectadas por un desastre, ya que muchas veces es imposible distribuir las ayudas a cada una de las familias damnificadas. Es importante considerar que estos centros de distribución suelen estar a muy poca distancia de la zona del desastre; no obstante, estos deben abastecerse desde un depósito central, utilizando una flota de vehículos heterogénea y capacitada. Los autores modelan el problema como una generalización del modelo de cobertura de recorrido, considerando entregas divididas y un enfoque de solución heurístico.

  A su vez, Rabta et al. (2018) elaboran un modelo de logística humanitaria para la distribución en la última milla mediante la utilización de drones, con los cuales se optimiza la entrega de paquetes livianos con artículos de ayuda como vacunas y tarjetas de purificación de agua, entre otros. El objetivo del modelo es minimizar la distancia total de viaje (tiempo/costo), teniendo en cuenta las restricciones de carga de energía de los drones, para permitir la extensión de la distancia de operación del dron. Se discute la implementación de diferentes políticas prioritarias a través de la construcción de varios escenarios teóricos. Asimismo, Ruiz y Ndoma (2019) evalúan el impacto que genera el uso de drones para la respuesta ante desastres naturales, considerando que estos se pueden utilizar principalmente para tres actividades: evaluación del daño de infraestructura generado por el desastre, entrega de ayudas humanitarias y evaluación post-aérea de cualquier desastre natural.

  Huang & Rafiei (2019) desarrollan un modelo de entrega de ayudas humanitarias, considerando una red de distribución de varios periodos, con ventanas de tiempo y entregas divididas. El modelo compara medidas de equidad con respecto a cantidades de entrega, tiempos de llegada y tiempos de privación en diferentes ubicaciones. Los autores encuentran que la equidad del tiempo de privación permite abordar mejor la distribución de emergencia humanitaria. El modelo fue probado en un caso simulado de estudio referido al terremoto de Haití de 2010, para ilustrar el impacto de las medidas de equidad propuestas.

  Aunque el enfoque de modelación matemática ha sido el más utilizado para abordar este tipo de temáticas, algunos autores como Gutjahr & Nolz (2016) realizan una revisión de literatura sobre los métodos de optimización multicriterio que se utilizan para la gestión de crisis humanitarias generadas por desastres naturales, epidemias y otras formas de crisis humanitarias. Asimismo, Wang & Zhang (2019) desarrollan un modelo de simulación basado en agentes para evaluar la capacidad de suministro de ayudas humanitarias, con el objetivo de dar soporte para la toma de decisiones. El modelo considera diferentes mecanismos de coordinación y transporte, para optimizar la capacidad de suministro de la red. Para evaluar la aplicabilidad del modelo, los autores utilizaron los datos recolectados sobre el suministro de petróleo refinado durante la emergencia provocada por el terremoto de Wenchuan, China, en 2008.

  Hoy en día, la teoría y práctica de la toma de decisiones multicriterio se encuentra dividida principalmente en dos vertientes: los métodos de decisión multiatributo y las técnicas de toma de decisiones multiobjetivo. Los problemas de decisión multiobjetivo plantean varios objetivos que deben optimizarse y que normalmente se encuentran en conflicto entre sí. Ferrer et al. (2018) desarrollaron un modelo de programación por metas para la optimización de criterios múltiples en la distribución de ayudas humanitarias en la última milla, considerando variables como tiempo de privación, costo, cobertura, equidad y seguridad. El modelo planteado fue validado utilizando datos de una inundación en Pakistán en 2010.

  Por el contrario, los problemas tradicionales de decisión multiatributo buscan seleccionar la mejor alternativa entre un conjunto de posibilidades, evaluando un grupo de atributos comunes desde la perspectiva de que, mediante la evaluación de valores de múltiples atributos, es posible tomar una decisión más razonable (Zhou et al., 2020). Para lograr este propósito se han planteado distintas metodologías, que se presentan en la tabla 1.

  Tabla 1

  Metodologías multicriterio más utilizadas

  Herramienta multicriterio	Ventajas	Artículos referentes
  Jerarquíaanalítica (AHP)	Establece una escala de valoración para los criterios (Escala Saaty).	Flores et al. (1992); Chen y Li (2008); Lyon y Lyon (2013); Balaji y Kumar (2014)
  TOPSIS	Más que una herramienta de selección es una metodología para ordenar las diferentes alternativas a evaluar	Bhattacharya et al. (2007)
  Lógica difusa (FUZZY)	Permite valorar criterios cualitativos a través de la definición de escalas subjetivas	Baykasoglu et al. (2016)
  Proceso analítico en red (ANP)	Se puede trabajar con criterios que no tienen que estar organizados en forma de jerarquía,	Falcone y Petrillo (2014)
  Despliegue de la función de calidad (QFD)	Tiene en cuenta las necesidades del cliente y las características propias de la organización a la hora de tomar la decisión,	Osorio et al. (2011) y Osorio et al. (2017)
  AHP-FUZZY	Permite manejar la incertidumbre de la valoración de los expertos a través de una escala de Saaty definida con números difusos	Chu et al. (2008); Cakir y Canbolat (2008)
  AHP-TOPSIS	La valoración de criterios se realiza utilizando el método tradicional de AHP y la evaluación de los ítems con TOPSIS permite ordenarlos según su importancia	Osorio y Manotas (2018); Henao et al., 2019
  QFD-FUZZY	Permite tener en cuenta escalas subjetivas en la valoración del QFD original	Osorio et al. (2011); Osorio et al. (2017)
  VIKOR	Es eficaz en aquellos casos en que, el decisor no es capaz o no sabe expresar sus preferencias al inicio del proceso.	Więckowski y Sałabun (2020); Bhalaji et al. (2020)
  PROMETHEE	Propone un procedimiento de cálculo transparente y fácil para entender para el decisor. Sin embargo, debe combinarse con un método viable para determinar los pesos de los criterios involucrados.	Makan y Fadili (2020)
  ELECTRE	Permite reducir el tamaño del conjunto de soluciones, mediante alternativas favorables y menos favorables a través del cálculo de un índice de concordancia/ discordancia.	Galo et al. (2018); Liu Wan (2019).

  Entre los estudios que han aplicado herramientas multicriterio en el contexto de entrega de ayudas humanitarias se encuentra el de Henao et al. (2019), quienes proponen un modelo de decisión multicriterio que integra los métodos AHP y TOPSIS, para que un banco de alimentos pueda administrar de la mejor manera posible los recursos disponibles. La herramienta de jerarquía analítica (AHP) es utilizada para ponderar los criterios que se consideran relevantes, y TOPSIS para valorar dichos criterios en cada una de las familias que solicitan el apoyo. El modelo desarrollado fue validado en un banco de alimentos en Colombia, que presentó resultados positivos a la hora de la priorización de las familias solicitantes. Por el contrario, en la presente investigación se utilizará la metodología multicriterio QFD Fuzzy, debido a que este método permite comprender la relación entre diferentes variables y los objetivos estratégicos del proceso en cuestión (Deveci et al., 2019). Se debe considerar que, para el caso particular a analizar, se busca definir el peso de las variables para la generación de un indicador de vulnerabilidad que permita atender al mayor número de familias afectadas de forma equitativa con el menor costo posible.

  Planteamiento del problema

  Según estadísticas del Departamento Administrativo Nacional de Estadística (DANE), en Colombia durante el periodo de noviembre de 2019 a enero del 2020 la ocupación de empleos informales fue del 47.7 %, lo que conlleva a que la decisión de confinamiento, emitida por el gobierno como medida preventiva para mitigar el riesgo de contagios por el covid-19, imposibilite la oportunidad de trabajo para un gran número de personas, ocasionando desabastecimiento de alimentos necesarios y productos básicos de la canasta familiar en familias donde la supervivencia depende de las ganancias obtenidas en el diario vivir.

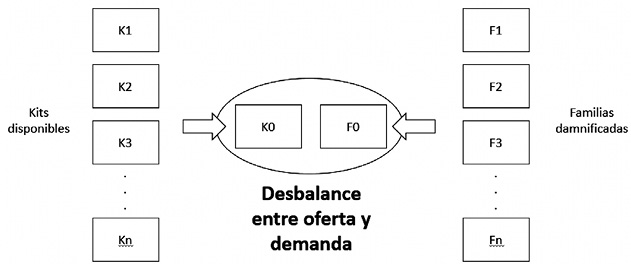
  Para aliviar este sufrimiento, el gobierno y las distintas alcaldías municipales han establecido la entrega de una serie de ayudas que permitan acceder a productos de primera necesidad a la población damnificada (UNGRD, 2020). Asimismo, estas entidades han destinado la entrega de kits de supervivencia básica a la población, pero se han enfrentado con el problema de que la demanda de remesas por parte de la población afectada es mucho mayor a la oferta de kits de supervivencia disponibles en el momento (ver figura 1). Por lo anterior, es necesario crear un modelo que permita establecer la rutina de entrega de productos a cada familia, teniendo en cuenta unos criterios de prioridad previamente establecidos. En este artículo de investigación se tomará como caso de estudio una ciudad del centro del Valle del Cauca, que actualmente tiene una población afectada de 15 000 familias, aproximadamente, y solo tiene una disponibilidad promedio quincenal de 3 000 kits de supervivencia.

  Figura 1

  Desbalance generado por el exceso de demanda de familias damnificadas ante una limitada oferta de kits de supervivencia

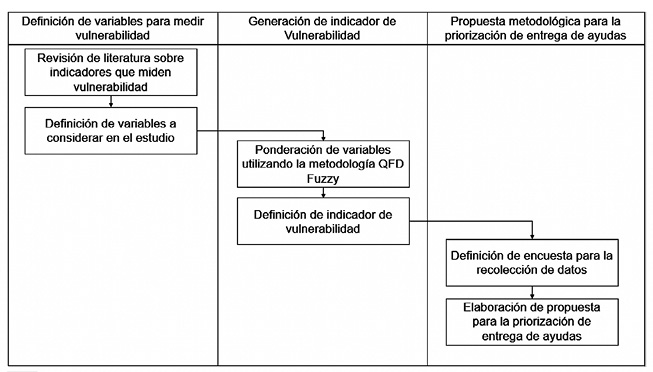
  Metodología

  La metodología para construir una herramienta de priorización para la asignación de ayudas humanitarias se desarrolla en tres fases principales (figura 2). La primera consistió en la definición de las variables a ser consideradas para medir la vulnerabilidad de las familias; para esto se realizó una revisión de literatura sobre los indicadores utilizados en la medición de población en situación de desastre. En la segunda fase se utilizó la herramienta multicriterio QFD Fuzzy para obtener una ponderación de las variables previamente seleccionadas, y en la última fase se abordó el diseño de una encuesta para la caracterización de la población, junto con la definición de indicadores por cada una de las variables, con el objetivo de establecer un puntaje de vulnerabilidad para cada familia que permita establecer una estrategia para la priorización de la entrega de ayudas humanitarias.

  Figura 2

  Metodología para desarrollar herramienta de priorización

  Resultados

  Fase 1. Definición de las variables para medir vulnerabilidad

  Para definir el grado de vulnerabilidad de una familia se realizó una revisión de los distintos indicadores propuestos por entidades gubernamentales como el Departamento Administrativo Nacional de Estadística (DANE) y el Sistema de Identificación de Potenciales Beneficiarios de Programas Sociales (SISBÉN), a partir de variables que buscan determinan las condiciones socioeconómicas, culturales, de educación y vivienda de cada grupo familiar. La tabla 2 resume las variables identificadas en los tres indicadores analizados.

  Tabla 2

  Variables utilizadas para la medición de indicadores de vulnerabilidad y pobreza

  Variable	Definición	Indicador Vulnerabilidad DANE	Indicador Pobreza Multidimensional DANE	Puntaje SISBÉN
  Comorbilidades	Hace relación a si hay personas en el grupo familiar a evaluar con enfermedades de base que las conviertan en población vulnerable y con mayor riesgo de muerte en caso de adquirir el virus covid-19.	X
  Individuos mayores de 60 años	Se refiere a la existencia de personas mayores de 60 años en un grupo familiar, que por su edad tienen un mayor riesgo a la exposición de virus covid-19.	X
  Hacinamiento	Es un indicador que se calcula con la relación entre las personas que habitan en una vivienda con el número de dormitorios disponibles dentro de la misma.	X	X	X
  Nivel de educación familiar	Calculado a partir de índices como inasistencia escolar, analfabetismo y bajos logros educativos.		X	X
  Tasa de dependencia económica	Indica el cociente de la división entre las personas en edades dependientes (menores de 15 y mayores de 60 años) con las personas en edades productivas.		X	X
  Empleo informal	Proporción de la Población Económicamente Activa (PEA) del hogar, que están ocupados y no cotizan en el fondo pensiones.		X
  Sin aseguramiento de salud	Proporción de miembros del hogar mayores de cinco años sin afiliación aseguridad social en salud.		X	X
  Discapacidad	Hace referencia al número de personas con discapacidad física o mental dentro del núcleo familiar.			X
  			Continua...
  ... viene
  Variable	Definición	Indicador Vulnerabilidad DANE	Indicador Pobreza Multidimensional DANE	Puntaje SISBÉN
  Estrato socioeconómico	Es una clasificación en estratos de los inmuebles residenciales que deben recibir servicios públicos.			X
  Número de personas en el hogar	Cantidad de personas que viven en una familia.		X	X

  Fase 2. Ponderación de variables

  Una vez definidas las variables iniciales del estudio, se aplicó una encuesta a los expertos académicos, sociales y con cargos públicos, con el objetivo de identificar la pertinencia de cada variable con la definición del indicador de vulnerabilidad por familia, además de obtener la relación entre los objetivos estratégicos del proceso y las variables. Lo anterior permitió la aplicación de la herramienta multicriterio QFD Fuzzy.

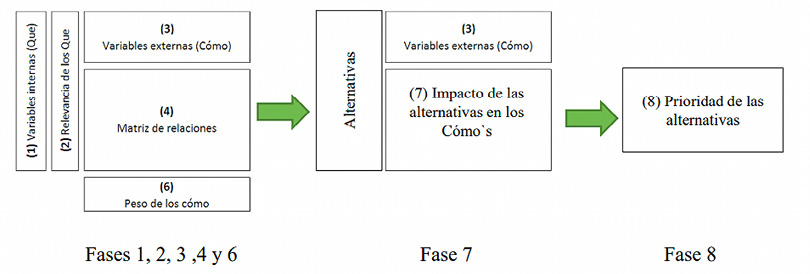
  La metodología QFD Fuzzy utilizada en esta investigación se basa en lo establecido por Bevilacqua et al. (2006), quienes definen ocho fases para la aplicación de la herramienta. En este estudio se aplicaron todas las fases, excepto la número 5, debido a que, en la situación particular, no se hace necesario medir la correlación de los objetivos estratégicos. Las etapas se muestran en la figura 3.

  Figura 3

  Aplicación de metodología QFD Fuzzy.

  Nota. Osorio Gómez (2011).

  Identificación de variables internas al proceso (los qué)

  Esta etapa determinó aquellos criterios generales que se deben considerar a la hora de realizar la distribución de ayudas humanitarias. En este caso, según la revisión de literatura realizada sobre estrategias de entrega en el ámbito de logística humanitaria, se identificaron las variables que se definen en la tabla 3.

  Tabla 3

  Variables internas del proceso (los qué)

  Q1	Equidad en las entregas.
  Q2	Cobertura de poblaciones afectadas.
  Q3	Tiempos de privación cortos.
  Q4	Eficiencia en costos.
  Q5	Entregas seguras.

  Calcular la importancia relativa de los qué

  Este paso necesitó la valoración de los siguientes expertos seleccionados: una magíster en ingeniería con experiencia en aplicación de herramientas multicriterio, el secretario de gestión del riesgo de la ciudad objeto de estudio y una magíster en derechos humanos experta en necesidades sociales relacionadas con temáticas de distribución de ayudas alimentarias en situaciones de desastre.

  Una vez aplicada la encuesta se obtuvieron los resultados presentados en la tabla 4. Se debe tener en cuenta que los expertos evaluaron la importancia de cada variable utilizando la escala lingüística definida por Bevilacqua et al. (2006). Luego de tener definidas las variables internas se procedió con la transformación de la escala lingüística, usando números difusos triangulares (ver tabla 5), y se aplicó la fórmula de la ecuación 1 para obtener el peso final de cada variable interna:

  Peso variable interna = Wi

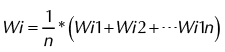  (1)

  Donde n equivale al número de expertos

  Tabla 4

  Valoración de las variables internas por parte de los expertos

  Qué	Evaluadores
  	1	2	3	Peso (Wi)
  Equidad en las entregas.	A	A	A	6	7	8
  Cobertura de poblaciones afectadas.	MA	M	MA	7	8	9
  Tiempos de privación cortos.	MA	MA	M	7	8	9
  Eficiencia en costos.	M	A	A	5	6	7
  Entregas seguras.	A	A	A	6	7	8

  Tabla 5

  Escala lingüística propuesta por Bevilacqua et al. (2006)

  Escala	Significado	Número difuso triangular
  MA	Muy alto	(8,9,10)
  A	Alto	(6,7,8)
  M	Medio	(4,5,6)
  B	Bajo	(2,3,4)
  MB	Muy bajo	(0,1,2)

  Identificar los objetivos estratégicos (los cómo)

  Los objetivos estratégicos se definieron a partir de la revisión de las misiones de organizaciones dedicadas a
  la entrega de ayudas humanitarias como la Cruz Roja y la Unidad Nacional para la Gestión del Riesgo de Desastres (UNGRD). La tabla 6 enseña los objetivos estratégicos definidos para la problemática en particular.

  Tabla 6

  Definición de objetivos estratégicos

  O1	Garantizar la seguridad alimentaria de la población afectada.
  O2	Distribuir equitativamente los kits alimenticios entre la población.
  O3	Establecer un orden de atención a las familias afectadas según sus necesidades.
  O4	Asegurar la mayor cobertura de la población.
  O5	Garantizar rutas de distribución seguras.

  Relación de los qué con los cómo

  Esta información se obtiene a partir de la encuesta, valorada con la misma escala lingüística presentada anteriormente. La tabla 7 presenta los resultados.

  Tabla 7

  Matriz de relación entre qué y cómo

  Objetivo 1

  Objetivo 2

  Objetivo 3

  Objetivo 4

  Objetivo 5

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  Q1

  MA

  MA

  MA

  MA

  A

  MA

  B

  A

  A

  M

  A

  A

  M

  B

  M

  Q2

  A

  A

  A

  MA

  A

  MA

  B

  B

  B

  MA

  MA

  MA

  M

  A

  M

  Q3

  MA

  A

  A

  B

  M

  M

  MA

  MA

  MA

  M

  B

  M

  M

  A

  M

  Q4

  M

  MA

  M

  M

  B

  B

  M

  A

  M

  M

  A

  B

  B

  MA

  B

  Q5

  M

  M

  M

  B

  B

  B

  M

  B

  M

  B

  B

  B

  MA

  MA

  MA

  Ponderación de los cómo

  Se transformaron las ponderaciones de la tabla 7 utilizando los números difusos triángulos presentes en la tabla 5, aplicando la ecuación 2. Los resultados se presentan en la tabla 8.

  Peso = Wj

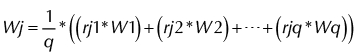  (2)

  qué = q; cómo =j

  Tabla 8

  Ponderación de los objetivos estratégicos (los cómo)

  	Peso (Wi)			Objetivo 1			Objetivo 2			Objetivo 3			Objetivo 4			Objetivo 5
  Q1	6	7	8	8	9	10	7	8	9	5	6	7	5	6	7	3	4	5
  Q2	7	8	9	6	7	8	7	8	9	5	6	7	8	9	10	5	6	7
  Q3	7	8	9	7	8	9	3	4	5	5	6	7	3	4	5	5	6	7
  Q4	5	6	7	5	6	7	3	4	5	3	4	5	4	5	6	4	5	6
  Q5	6	7	8	4	5	6	2	3	4	3	4	5	2	3	4	8	9	10
  	Peso (Wj)			37	43	49	28	34	41	26	32	38	28	34	40	30	36	43

  Determinación de la correlación entre las variables y los cómo

  En la encuesta realizada a los tres expertos se les solicitó validar la pertinencia de las variables definidas previamente. Se debe aclarar que solo se consideraron en el estudio aquellas variables que obtuvieron una aprobación por parte de dos de los tres evaluadores; por tal motivo, se descartaron tres de las diez variables: discapacidad, nivel de escolaridad de la familia y número de integrantes del hogar. Partiendo de esto se obtuvo la matriz de relación entre variables y los objetivos estratégicos, tal y como lo muestra la tabla 9.

  Tabla 9

  Matriz de relación entre las variables y los objetivos estratégicos

  Variables

  Objetivo 1

  Objetivo 2

  Objetivo 3

  Objetivo 4

  Objetivo 5

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  E1

  E2

  E3

  Comorbilidades

  MA

  M

  MA

  MA

  B

  M

  A

  MB

  B

  A

  MB

  A

  B

  A

  M

  Individuos mayores de 60 años

  MA

  M

  MA

  MA

  B

  A

  B

  MB

  B

  A

  MB

  MA

  B

  A

  M

  Hacinamiento

  A

  MA

  A

  B

  MA

  A

  B

  MB

  B

  M

  A

  A

  B

  A

  M

  Tasa de dependencia económica

  MA

  A

  MA

  MA

  MA

  M

  B

  B

  B

  MA

  A

  A

  A

  A

  A

  Empleo informal

  MA

  MA

  MA

  MA

  MA

  A

  B

  M

  M

  MA

  A

  A

  A

  A

  A

  Sin aseguramiento de salud

  A

  A

  A

  B

  A

  B

  B

  M

  A

  M

  A

  M

  B

  A

  M

  Estrato socioeconómico

  A

  A

  A

  A

  A

  M

  B

  A

  A

  M

  A

  M

  A

  A

  A

  Ponderación de las variables

  Se transformó la tabla 9 a números difusos triangulares y se calculó la media geométrica de los datos. Luego se aplicó la ecuación 3 para hallar la prioridad de cada variable y, con base a ella, calcular su peso. La tabla 10 presenta el índice de prioridad y el peso final de cada variable dentro del indicador de vulnerabilidad propuesto.

  IRhj: j equivale a los cómo y h a las variables

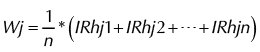  (3)

  Donde n equivale al número de expertos

  Tabla 10

  Ponderación de variables en el indicador de vulnerabilidad

  Variables	Índice de prioridad	Peso
  Comorbilidades	212.8	12.9 %
  Individuos mayores de 60 años	213.454	13.0 %
  Hacinamiento	218.253	13.3 %
  Tasa de dependencia económica	263.264	16.0 %
  Empleo informal	283.054	17.2 %
  Sin aseguramiento de salud	210.911	12.8 %
  Estrato socioeconómico	245.112	14.8 %

  Con los pesos obtenidos en la tabla 10 se procedió a construir un indicador de vulnerabilidad a partir de la información de cada familia; para poder realizar este cálculo se consolidaron las respuestas de la encuesta aplicada a la población, con el objetivo de determinar el orden de entrega de las ayudas.

  Fase 3. Establecimiento de la metodología para la priorización de la entrega de ayudas humanitarias

  En esta fase se diseñó la encuesta de caracterización de la población, con la cual se construyó el indicador para cada una de las siete variables definidas, con el propósito de establecer una escala que permita obtener un puntaje de vulnerabilidad útil para establecer el orden de entrega de las ayudas humanitarias. La tabla 11 presenta los indicadores definidos por cada variable, junto con la fórmula para realizar el cálculo.

  Tabla 11

  Indicadores definidos por variables de vulnerabilidad

  Variable	Indicador	Fórmula
  Comorbilidades	% de personas con comorbilidades	Número de personas con comorbilidades/Total integrantes.
  Variable	Indicador	Fórmula
  Individuos mayores de 60 años	% de personas mayores de 60 años	Número de personas mayores 60 años/Total integrantes.
  Hacinamiento	% de hacinamiento	Total integrantes de la familia/Número dormitorios de la casa.
  Tasa de dependencia económica	% de la tasa de dependencia económica	Cantidad de niños y personas mayores de 60 años/Cantidad personas en edad de trabajar.
  Empleo informal	% de personas con trabajo informal	Número de personas con empleo informal/Total integrantes.
  Sin aseguramiento de la salud	% de personas sin aseguramiento de salud	Cantidad de personas sin aseguramiento/Total integrantes.
  Estrato socioeconómico	Estrato socioeconómico	Estrato socioeconómico de la vivienda.

  Asimismo, se definió para cada indicador una puntuación en escala numérica del 1 al 5, donde 5 representa mayor vulnerabilidad y 1 hace referencia a una inseguridad menor. La tabla 12 resume las escalas propuestas.

  Tabla 12

  Escalas numéricas propuestas por cada indicador

  Indicador	Escala
  	5	4	3	2	1
  % de personas con comorbilidades	X ≥ 75 %	50 % ≤ X < 75 %	25 % ≤ X < 50 %	10 % ≤ X < 25 %	X < 10 %
  % de personas mayores de 60 años	X ≥ 75 %	50 % ≤ X < 75 %	25 % ≤ X < 50 %	10 % ≤ X < 25 %	X < 10 %
  Hacinamiento	X > 5	NA	2.4 < X ≤ 4.9	NA	X ≤ 2.4
  Tasa de dependencia económica	X ≥ 75 %	50 % ≤ X < 75 %	25 % ≤ X < 50 %	10 % ≤ X < 25 %	X < 10 %
  % de personas con trabajo informal	X ≥ 75 %	50 % ≤ X < 75 %	25 % ≤ X < 50 %	10 % ≤ X < 25 %	X < 10 %
  % de personas sin aseguramiento de salud	X ≥ 75 %	50 % ≤ X < 75 %	25 % ≤ X < 50 %	10 % ≤ X < 25 %	X < 10 %
  Estrato socioeconómico	1	2	3	4	> 4

  Para realizar la prueba de validez, se generaron datos sintéticos que permitieron diligenciar la encuesta de caracterización de la población en una muestra inicial de 1000 familias utilizando la simulación Montecarlo. Con base en los pesos y las variables obtenidas en la fase 2 (ver tabla 10), y teniendo en cuenta la escala presentada en la tabla 12, se obtuvo un puntaje que asocia las condiciones de vulnerabilidad de las familias simuladas.
  En la tabla 13 se muestra el número de familias que obtuvieron un puntaje mayor que 4 (de atención prioritaria), las que obtuvieron una calificación entre 3 y 4 (prioridad media) y, finalmente, las familias menos vulnerables (puntaje inferior a 3). Es necesario aclarar que la herramienta diseñada puede ser utilizada para evaluar un número de familias más grande, con el objetivo de ayudar a los gobiernos locales a establecer el orden de entrega de las ayudas humanitarias disponibles.

  Tabla 13

  Categorías de vulnerabilidad por familia

  Tipo de vulnerabilidad	Número de familias
  Alta (X ≥ 4)	21
  Media (3 < X < 4)	564
  Baja (X ≤ 3)	415

  A partir de las pruebas realizadas se resume que la metodología, aplicada al instrumento diseñado, incluye la ponderación de las variables que definen la vulnerabilidad de una población; aunque es cierto que las administraciones locales pueden utilizar los resultados obtenidos en este artículo luego de la aplicación QFD Fuzzy, también podrían determinar los pesos de cada variable dependiendo de los intereses particulares del alcalde de la ciudad. Por ejemplo, puede suceder que para una ciudad sea más prioritario atender de forma ágil a aquellas familias que tienen integrantes con empleo informal o con un estrato socioeconómico bajo. Después de ponderar las variables, se debe aplicar una encuesta de caracterización que permita calcular los indicadores definidos para cada una (tabla 11). Por último, una vez se tienen los datos de la población, se procede a realizar la puntuación de cada variable utilizando la escala definida en la tabla 12 y se multiplica por el peso dado a la variable, con el objetivo de obtener un puntaje final que represente el grado de vulnerabilidad de cada familia, de tal forma que este resultado permita a la administración municipal atender inicialmente a aquellas familias cuyo indicador sea mayor.

  Conclusiones

  Las variables de vulnerabilidad consideradas en el estudio permiten la agrupación de familias priorizadas, lo que efectivamente establece, de acuerdo con los criterios definidos, una asignación más equitativa que mitiga el riesgo de falta de pertinencia y efectiva atención a las familias afectadas. La metodología ofrece una estructura consecuente con aspectos estratégicos claves, formulados por diferentes instancias internacionales, que buscan asegurar una cobertura objetivo y seguridad alimentaria, entre otros aspectos. Sin embargo, es importante considerar las limitaciones propias del sistema, en tanto que, al no disponer de recursos ilimitados, es imposible garantizar la cobertura total, debido a que la demanda excede notoriamente el número de kits alimentarios disponibles. El aporte más importante que la metodología propuesta ofrece es que, frente a una oferta limitada, se logra establecer de manera rigurosa la estructura de asignación de kits alimenticios con una cobertura más efectiva, en comparación con la que se obtiene mediante la asignación empírica no estructurada.

  La vulnerabilidad en este estudio consideró variables que han sido tratadas en diversas investigaciones; sin embargo, el aporte metodológico que propone la integración de estas variables, con el uso de la herramienta QFD y su valoración difusa, permite visualizar notorias diferencias en la población frente a la categorización de un estado de vulnerabilidad. Fue un gran reto establecer las variables que representan la diversidad de las familias valoradas, pues la estructura familiar es distinta en cada caso y, en el contexto de la pandemia covid-19, pueden considerarse como más vulnerables en función de la edad y las preexistencias de sus integrantes, entre otros aspectos. En este sentido, la valoración difusa permite establecer rangos que facilitan
  la inclusión en el análisis de estas condiciones particulares. No se identificó en la literatura revisada una estrategia similar que permitiera apoyar la toma de decisiones para la asignación priorizada de ayudas.

  Otro aspecto relevante durante el desarrollo de esta investigación está relacionado con las diferentes medidas de vulnerabilidad. Se hizo evidente la mirada divergente de algunas fuentes, que en cualquier caso fue necesario considerar en esta investigación, donde además se involucraron los indicadores de vulnerabilidad y pobreza multidimensional propuestos por entidades gubernamentales como el DANE y el SISBÉN. No obstante, es necesario entender la lógica evolutiva de estos indicadores, dada la complejidad que supone la dinámica social, lo que obliga a que herramientas como las utilizadas en esta investigación sean actualizadas frecuentemente para considerar todas las dimensiones que surjan para la valoración del bienestar de la sociedad.

  En todo caso, se estableció que esta metodología ofrece al gobierno mayor efectividad en la toma de decisiones, a fin de atender una emergencia sanitaria como la ocasionada por el covid-19. Aun así, es necesario insistir que no se trata de una metodología estática, sino que se requiere tener en cuenta las nuevas variables que puedan
  surgir como indicadores de vulnerabilidad. Esto se presenta como una investigación futura complementaria.

  Por último, esta investigación desarrolla un marco metodológico que puede ser replicado por otras ciudades, a nivel nacional e internacional, dado que se valora como de gran apoyo en el cumplimiento del objetivo de priorizar la entrega de ayudas humanitarias de manera más efectiva.

  Referencias

  Balaji, K., & Kumar, V. S. S. (2014). Multicriteria Inventory ABC Classification in an Automobile Rubber Components Manufacturing Industry. Procedia CIRP, 17, 463-468. https://doi.org/10.1016/j.procir.2014.02.044

  Balcik, B., Beamon, B. M., & Smilowitz, K. (2008). Last mile distribution in humanitarian relief. Journal of Intelligent Transportation Systems: Technology, Planning, and Operations, 12(2), 51-63. https://doi.org/10.1080/15472450802023329

  Baykasoglu, A., Subulan, K., & Karaslan, F. S. (2016). A new fuzzy linear assignment method for multi-attribute decision making with an application to spare parts inventory classification. Applied Soft Computing, 42, 1-17. https://doi.org/10.1016/j.asoc.2016.01.031

  Bevilacqua, M., Ciarapica, F. E., & Giacchetta, G. (2006). A fuzzy-QFD approach to supplier selection, 12, 14-27. https://doi.org/10.1016/j.pursup.2006.02.001

  Bhalaji, R. K. A., Bathrinath, S., & Saravanasankar, S. (2020). A Fuzzy VIKOR method to analyze the risks in lean manufacturing implementation. Materials Today: Proceedings. https://doi.org/10.1016/j.matpr.2020.05.123

  Bhattacharya, A., Sarkar, B., & Mukherjee, S. (2007). Distance-based consensus method for ABC analysis. International Journal of Production Research, 45(15), 3405-3420. https://doi.org/10.1080/00207540600847145

  Cakir, O., & Canbolat, M. S. (2008). A web-based decision support system for multi-criteria inventory classification using fuzzy AHP methodology. Expert Systems with Applications, 35(3), 1367-1378. https://doi.org/10.1016/j.eswa.2007.08.041

  Chen, Y., Li, K. W., & Liu, S. (2008). A Comparative Study on Multicriteria ABC Analysis in Inventory Management. 2008 IEEE International Conference on Systems, Man and Cybernetics, 3280-3285.

  Chu, C. W., Liang, G. S., & Liao, C. T. (2008). Controlling inventory by combining ABC analysis and fuzzy classification. Computers and Industrial Engineering, 55(4), 841-851. https://doi.org/10.1016/j.cie.2008.03.006

  Deveci, M., Öner, S. C., Canıtez, F., & Öner, M. (2019). Evaluation of service quality in public bus transportation using interval- valued intuitionistic fuzzy QFD methodology. Research in Transportation Business & Management, 33. https://doi.org/10.1016/j.rtbm.2019.100387

  Falcone, D., De Felice, F., Forcina, A., Silvestri, A., & Petrillo, A. (2014). Inventory management using both quantitative and qualitative criteria in manufacturing system. IFAC Proceedings Volumes, 47(3). https://doi.org/10.3182/20140824-6-ZA-1003.02279

  Ferrer, J. M., Martín-Campo, F. J., Ortuño, M. T., Pedraza-Martínez, A. J., Tirado, G., & Vitoriano, B. (2018). Multi-criteria optimization for last mile distribution of disaster relief aid: Test cases and applications. European Journal of Operational Research, 269(2), 501-515. https://doi.org/10.1016/j.ejor.2018.02.043

  Flores, B. E., Olson, D. L., & Dorai, V. K. (1992). Management inventory of multicriteria classification. Mathematical and Computer Modelling, 16(12), 71-82. https://doi.org/10.1016/0895-7177(92)90021-C

  Galo, N. R., Daniel, L., Rosso, D., Cesar, L., & Carpinetti, R. (2018). A group decision approach for supplier categorization based on hesitant fuzzy and ELECTRE TRI. International Journal of Production Economics, 202, 182-196. https://doi.org/10.1016/j.ijpe.2018.05.023

  Gutjahr, W. J., & Nolz, P. C. (2016). Multicriteria optimization in humanitarian aid. European Journal of Operational Research, 252, 351-366. https://doi.org/10.1016/j.ejor.2015.12.035

  Hashemi, S. H., Tavana, M., & Abdi, M. (2020). A comprehensive framework for analyzing challenges in humanitarian supply chain management : A case study of the Iranian Red Crescent Society. International Journal of Disaster Risk Reduction, 42. https://doi.org/10.1016/j.ijdrr.2019.101340

  Henao, D., López, F., Chud Pantoja, V. L., & Osorio, J. C. (2019). Priorización multicriterio para la afiliación a un banco de alimentos en Colombia. Revista Logos, Ciencia & Tecnología, 12(1), 58-70. https://doi.org/10.22335/rlct.v12i1.1024

  Huang, K., & Rafiei, R. (2019). Equitable last mile distribution in emergency response. Computers and Industrial Engineering, 127, 887-900.

  Li, X., Ramshani, M., & Huang, Y. (2018). Cooperative maximal covering models for humanitarian relief chain management. Computers & Industrial Engineering, 119, 301-308. https://doi.org/10.1016/j.cie.2018.04.004

  Liu, X., & Wan, S. ping. (2019). A method to calculate the ranges of criteria weights in ELECTRE I and II methods. Computers and Industrial Engineering, 137. https://doi.org/10.1016/j.cie.2019.106067

  Makan, A., & Fadili, A. (2020). Sustainability assessment of large-scale composting technologies using PROMETHEE method. Journal of Cleaner Production, 261. https://doi.org/10.1016/j.jclepro.2020.121244

  Mary, S., & Mishra, A. K. (2020). Humanitarian food aid and civil conflict. World Development, 126. https://doi.org/10.1016/j.worlddev.2019.104713

  Naji-azimi, Z., Renaud, J., Ruiz, A., & Salari, M. (2012). A covering tour approach to the location of satellite distribution centers to supply humanitarian aid. European Journal of Operational Research, 222(3), 596-605. https://doi.org/10.1016/j.ejor.2012.05.001

  Osorio Gómez, J. C. (2011). Fuzzy QFD for multicriteria decision making - Application example. Prospectiva, 9(2), 22-29.

  Osorio, J. C., Arango, D. C., & Ruales, C. E. (2011). Selección de proveedores usando el despliegue de la función de calidad difusa. Revista EIA, 15, 73-83.

  Osorio, J. C., Manotas, D. F., & Rivera, L. (2017). Priorización de Riesgos Operacionales para un Proveedor de Tercera Parte Logística - 3PL. Información Tecnológica, 28(4), 135-144. https://doi.org/10.4067/S0718-07642017000400016

  Osorio, J. C., & Manotas, D. F. (2018). AHP Topsis para la selección de proveedores considerando el riesgo asociado a la calidad. Espacios, 39(16).

  Rabta, B., Wankmüller, C., & Reiner, G. (2018). A drone fleet model for last-mile distribution in disaster relief operations. International Journal of Disaster Risk Reduction, 28, 107-112. https://doi.org/10.1016/j.ijdrr.2018.02.020

  Ruiz-Estrada, M. A., & Ndoma, A. (2019). The uses of unmanned aerial vehicles – UAV ’ s- ( or drones ) in social logistic : disasters and humanitarian relief aid. Procedia Computer Science, 149, 375-383. https://doi.org/10.1016/j.procs.2019.01.151

  Shao, J., Wang, X., Liang, C., & Holguín-Veras, J. (2019). Research progress on deprivation costs in humanitarian logistics. International Journal of Disaster Risk Reduction, 42. https://doi.org/10.1016/j.ijdrr.2019.101343

  Suzuki, Y. (2019). Impact of material convergence on last-mile distribution in humanitarian logistics. International Journal of Production Economics, 223. https://doi.org/10.1016/j.ijpe.2019.107515

  UNGRD. (2020). Informe Operación COVID-19. http://portal.gestiondelriesgo.gov.co/Paginas/Slide_home/Informe-Operacion-COVID-19.aspx

  Wang, Z., & Zhang, J. (2019). Agent-based evaluation of humanitarian relief goods supply capability. International Journal of Disaster Risk Reduction, 36. https://doi.org/10.1016/j.ijdrr.2019.101105

  Więckowski, J., & Sałabun, W. (2020). How the normalization of the the decision decision influences influences the results in the VIKOR method ? Procedia Computer Science, 176, 2222-2231. https://doi.org/10.1016/j.procs.2020.09.259

  Zhou, S., Ji, X., & Xu, X. (2020). A hierarchical selection algorithm for multiple attributes decision making with large-scale alternatives. Information Sciences, 521, 195-208. https://doi.org/10.1016/j.ins.2020.02.030